Mesh d-refinement: a data-based computational framework to account for complex material response

Abstract: Model-free data-driven computational mechanics (DDCM) is a new paradigm for simulations in solid mechanics. The modeling step associated to the definition of a material constitutive law is circumvented through the introduction of an abstract phase space in which, following a pre-defined rule, physically-admissible states are matched to observed material response data (coming from either experiments or lower-scale simulations). In terms of computational resources, the search procedure that performs these matches is the most onerous step in the algorithm. One of the main advantages of DDCM is the fact that it avoids regression-based, bias-prone constitutive modeling. However, many materials do display a simple linear response in the small-strain regime while also presenting complex behavior after a certain deformation threshold. Motivated by this fact, we present a novel refinement technique that turns regular elements (equipped with a linear-elastic constitutive law) into data-driven ones if they are expected to surpass the threshold known to trigger material non-linear response. We term this technique data refinement'',d-refinement'' for short. Starting from an initially regular FEM mesh, the proposed algorithm detects where the refinement is needed and iterates until all elements presumed to display non-linearity become data-driven ones. Insertion criteria are discussed. The scheme is well-suited for simulations that feature non-linear response in relatively small portions of the domain while the rest remains linear-elastic. The method is validated against a traditional incremental solver (i.e., Newton-Raphson method) and we show that the d-refinement framework can outperform it in terms of speed at no loss of accuracy. We provide an application that showcases the advantage of the new method: bridging scales in architected metamaterials.

• The paper introduces a hybrid FEM and data-driven approach that leverages mesh d-refinement to transition elements into data-based simulations for non-linear behavior.
• The methodology employs iterative phase space convergence and clustering techniques to reduce computational cost while preserving accuracy.
• The approach is validated through simulations on architected metamaterials, demonstrating efficient stress field analysis and crack prediction.

Detailed Summary of "Mesh d-refinement: a data-based computational framework to account for complex material response"

Introduction to Data-Driven Computational Mechanics

Data-driven computational mechanics (DDCM) presents an alternative to traditional numerical simulations in solid mechanics, foreseeing a shift away from constitutive modeling interventions toward directly utilizing observed data. By deploying phase space representations, DDCM maps material responses without regressional bias, offering computational efficiency at scale when accessing both experimental insights and simulations.

DDCM has proven versatile through incorporation into small-strain dynamics and large deformation contexts. However, adoption has been throttled by computation-intensive methodologies central to phase space traversal. The emergence and paradigmatic merits of DDCM center around the circumvention of phenomenological assumptions frequently accompanying intricate material laws.

The Concept of Mesh d-Refinement

Introducing "d-refinement" or data refinement denotes a transformative approach tailored for cases where non-linearity surfaces amidst predominantly linear elasticity domains. The technique expedites traditional FEM scenarios by converting elements presumed to exhibit non-linear behavior—determined via specialized criteria—to data-driven formulations. This dynamic adaptation thrives on a two-stage iterative convergence strategy until dataset elements transition robustly to DD states.

FEM-DD Coupling Strategy

Our approach amalgamates FEM and DD elements into a coherent computational framework, distinguishing subsets S1 and S2 of the element space. S1 encompasses traditional model elements, while S2 adopts DD representations. Element states in phase space are dynamically governed by both contrived constitutive equations and adjacency assignments based on applicable stress/strain data points.

The iteration driven by DD searches guarantees convergence through compliance reconciling closest dataset points within the phase space manifold intersection. Here, the flexibility in employing environmental datasets provides avenues for algorithmic efficiency escalation notably when navigating large phase spaces, with optimization adaptable through cluster-based techniques such as k-d trees.

Implementation and Numerical Validation

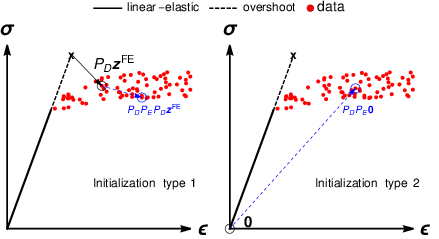
Figure 1: Schematic representation of DD element initialization possibilities on a 2D phase space. The first circle (black) represents the initialization point and the second one (blue) the point in the dataset that the algorithm converges to in the next iteration (see that each method may pick a different datum after the iteration).

Kernel experimentation for method validation involved computational exercises targeting stress fields around geometrical discontinuities, notably with 3D trusses and 2D plates featuring stress concentrations. D-refinement emerges as computationally proficient, preserving requisite accuracy while significantly outperforming traditional incremental solvers in wall-clock time, especially evident in quantitative workload reduction.

Application to Architected Metamaterials

The multiscale application of d-refinement leverages material data for predictions on architected metamaterials. Formerly bound by restrictive data synthesis and constitutive model developments, d-refinement renders scale-bridging feasible sans assumption-laden modeling. In one depicted case, TMPTA materials within octet-truss frameworks illuminate stress redistribution post-crack initiation—a relevant insight in fracture process zone vis-à-vis linear-elastic predictions.

Figure 2: Scheme of the scale bridging procedure (from left to right): rod material dataset is used to characterize the response of octet-truss unit cell using DDCM, these RVE simulations yield linear-elastic constants and a non-linear material-response dataset used for macroscale simulations of a cubic sample of architected material using d-refinement.

Concluding Remarks

Mesh d-refinement embodies a promising computational alternative harnessing efficient phase space navigation to tackle complex mechanical problems with non-linear traits. Whether applied in traditional simulations or pioneering multiscale studies, d-refinement anchors immense potential for future developments considering dynamics and path-dependent phenomena.

As robustness enhances alongside distributed computational paradigms, consideration should extend toward path-dependent systems modeling externalities, amending load intricacies from material histories. Future efforts will likely emphasize dynamic load paths, unraveling further robustness avenues inherent within second-generation data-driven solvers.