FE${}^\textbf{ANN}$ $-$ An efficient data-driven multiscale approach based on physics-constrained neural networks and automated data mining

Abstract: Herein, we present a new data-driven multiscale framework called FE${}^\text{ANN}$ which is based on two main keystones: the usage of physics-constrained artificial neural networks (ANNs) as macroscopic surrogate models and an autonomous data mining process. Our approach allows the efficient simulation of materials with complex underlying microstructures which reveal an overall anisotropic and nonlinear behavior on the macroscale. Thereby, we restrict ourselves to finite strain hyperelasticity problems for now. By using a set of problem specific invariants as the input of the ANN and the Helmholtz free energy density as the output, several physical principles, e.g., objectivity, material symmetry, compatibility with the balance of angular momentum and thermodynamic consistency are fulfilled a priori. The necessary data for the training of the ANN-based surrogate model, i.e., macroscopic deformations and corresponding stresses, are collected via computational homogenization of representative volume elements (RVEs). Thereby, the core feature of the approach is given by a completely autonomous mining of the required data set within an overall loop. In each iteration of the loop, new data are generated by gathering the macroscopic deformation states from the macroscopic finite element (FE) simulation and a subsequently sorting by using the anisotropy class of the considered material. Finally, all unknown deformations are prescribed in the RVE simulation to get the corresponding stresses and thus to extend the data set. The proposed framework consequently allows to reduce the number of time-consuming microscale simulations to a minimum. It is exemplarily applied to several descriptive examples, where a fiber reinforced composite with a highly nonlinear Ogden-type behavior of the individual components is considered.

• The paper presents a multiscale simulation framework using physics-constrained ANNs coupled with autonomous invariant-space data mining to reduce computational cost.
• It demonstrates high accuracy with ANN predictions matching RVE reference stresses within approximately 2% error across diverse deformation states.
• Scalable implementation and rapid convergence across geometries illustrate practical benefits in simulating complex fiber-reinforced hyperelastic materials.

Data-Driven Multiscale Modeling via Physics-Constrained Neural Networks and Automated Data Mining

Introduction and Motivation

The FE${}^\text{ANN}$ framework enables efficient multiscale simulations of materials with complex microstructure, focusing on nonlinear and anisotropic finite strain hyperelasticity. The approach addresses the prohibitive computational cost of coupled multiscale methods (e.g., FE${}^2$) and the challenges of surrogate model formulation in decoupled schemes by leveraging a physics-constrained artificial neural network (ANN) as a macroscopic constitutive surrogate and an autonomous data-mining loop for dataset enrichment.

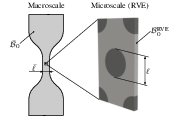
Figure 1: Schematic depiction of micro- and macroscale within a multiscale problem; scale separation $\bar \ell \gg \ell$ is required.

This methodology is tailored for hyperelastic solids and ensures the satisfaction of physical principles (objectivity, material symmetry, compatibility with balance of angular momentum, thermodynamic consistency) by selecting problem-specific invariants as ANN inputs and the Helmholtz free energy as output.

Multiscale Framework Overview

FE${}^\text{ANN}$ is a sequential multiscale strategy. At each iteration, the macroscopic FE simulation provides new states of deformation encountered in the problem. These are analyzed, mapped into an invariant space reflecting the material symmetry group, and unique states are automatically detected. Unknown states are then imposed at the microscale (RVE) to generate stress responses through computational homogenization. The data set is autonomously enriched and used to retrain the physics-constrained ANN surrogate.

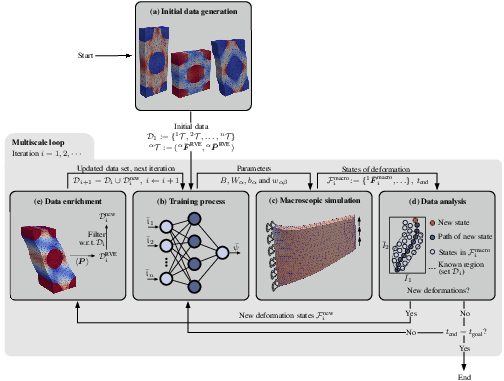
Figure 2: Schematic representation of the FE${}^\text{ANN}$ workflow, showing stages in data generation, ANN training, simulation, data analysis, and enrichment.

A Python/HPC implementation leverages SLURM batch scheduling for parallel execution of loop stages, enabling scalable multiscale simulation.

Physics-Constrained ANN Surrogate Model

The surrogate model is constructed as a feed-forward neural network (FNN) with one or more hidden layers. Its input vector consists of problem-specific tensor invariants, e.g., for transversely isotropic hyperelasticity, invariants such as $I_1$, $I_2$, $I_3$, $I_4 = \mathbf{M} : \mathbf{C}$, $I_5 = \mathbf{M} : \mathbf{C}^2$ (where $\mathbf{M} = \mathbf{A} \otimes \mathbf{A}$ encodes fiber direction).

Figure 3: Network structure for the physics-constrained macroscopic surrogate; normalized invariants are mapped to the ANN input.

The output is the macroscopic Helmholtz free energy $\psi$, from which associated stresses are computed via automatic differentiation:

$$\mathbf{T} = \sum_{\alpha} 2 \frac{\partial \psi}{\partial I_\alpha} \frac{\partial I_\alpha}{\partial \mathbf{C}}$$

Training minimizes stress errors, employing Sobolev-type loss functions, with the SLSQP optimizer and optional constraints to enforce growth and normalization conditions.

Autonomous Data Mining and Dataset Enrichment

During simulation, the physical state at each integration point is characterized by collecting deformation gradients and mapping them to invariant space. Unique states (outside the current data set under a prescribed tolerance) are automatically detected and their full time series are extracted for RVE homogenization. This approach ensures minimum redundant microscale solves and optimally populates the invariant manifold relevant to the macroscopic deformation history.

Figure 4: Autonomous sampling procedure shows expansion of relevant region in the invariant space for the cuboid tension case.

Data enrichment and filtering in invariant space further improve dataset efficiency and remove redundant RVE evaluations.

Numerical Implementation and Applications

The methodology was validated through three representative macroscopic geometries:

• Cuboid under tension
• Torsional sample
• Cook’s membrane

All samples employ a fiber-reinforced composite with pronounced nonlinearity at the microscale, modeled via a multi-parameter Ogden-type hyperelastic law. The RVE is constructed using stochastic fiber placement, facilitating transverse isotropy under finite strains (as opposed to regular unit cell geometries, which lose intended symmetry under finite deformations).

Figure 5: Effective stress-stretch curves from RVE homogenization and geometry of the stochastic periodic RVE with fibers.

Figure 6: Macroscopic geometries, BCs, and fiber directions for the test problems.

For each case, the multiscale algorithm demonstrated rapid convergence (few iterations) with minimal micro-scale solves, owing to the invariant-space data mining; the initial RVE data set (spanning major loading paths) was sufficient to bootstrap the surrogate model, which was then refined by new states encountered during simulation. Invariant-space overlap between disparate macroscopic deformations resulted in immediate transferability of RVE data between cases.

Figure 7: Last iteration's invariant space for the cuboid tension problem, showing final data coverage and macroscopic field distribution.

Validation showed that ANN surrogate predictions agreed with RVE-generated reference stresses to within $\sim 2\%$ error for stress field components, even for deformation states not in the training set.

Figure 8: ANN predictions against RVE references for both training/test splits and novel deformation states.

Robust transfer learning was observed when initial datasets for new geometries reused data mined from prior problems; e.g., in the torsion and Cook cases, iterations terminated quickly as most invariant states were already available.

Figure 9: Invariant-space coverage for the torsional sample; prior cuboid data enables immediate prediction without extensive new RVE calculations.

Macroscopic stress and deformation fields obtained with the surrogate matched reference solutions closely:

(Figure 10)

Figure 10: Macroscopic stress and right Cauchy-Green deformation distribution in the torsional sample’s final configuration.

Model Performance, Constraints, and Trade-Offs

The physics-constrained ANN architecture ensures physical admissibility, generalization outside training states, and efficient transfer between problems. While repeated retraining remains necessary as new invariant states are discovered, the autonomous data mining loop dramatically reduces microscale computational burden compared to classical approaches.

For further improvement, incorporating constraints on network weights can strictly enforce growth conditions (energy divergence for infinite or vanishing volume), though empirical results showed a trade-off: unconstrained training provided higher accuracy for surrogate stress prediction, at the cost of potential extrapolation risk for extreme states.

Implications and Future Directions

FE${}^\text{ANN}$ drastically reduces the number of required microscale simulations in multiscale material modeling, especially for complex geometries and loading states. Automated invariant-space sampling ensures efficient coverage of relevant deformation regions with minimal human intervention, enabling robust surrogate construction for highly nonlinear anisotropic materials.

Extending the method to different material symmetry groups requires inclusion of the corresponding invariant sets. Expansion to dissipative constitutive response (viscoelasticity, plasticity) demands architectures and loss formulations capable of handling history dependence and path memory. Integration with adaptive mesh refinement and uncertainty quantification frameworks may yield further robustness.

Furthermore, this approach is suitable for scalable implementations on high-performance clusters and is directly compatible with existing FE toolchains via user-defined material models employing automatic differentiation.

Conclusion

The FE${}^\text{ANN}$ framework presents a comprehensive data-driven multiscale strategy leveraging physics-constrained neural surrogates and fully unsupervised, invariant-space data mining to efficiently simulate macroscale behavior of materials with complex microstructure. The approach achieves high accuracy, computational efficiency, and generalizes effectively to novel loading paths and geometries, with direct applicability to large-scale engineering analysis and material design. Future work will address more general symmetry groups, dissipative mechanisms, and further automation of surrogate construction for enhanced predictive capability.