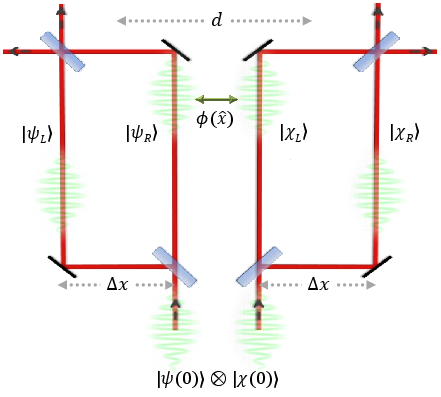
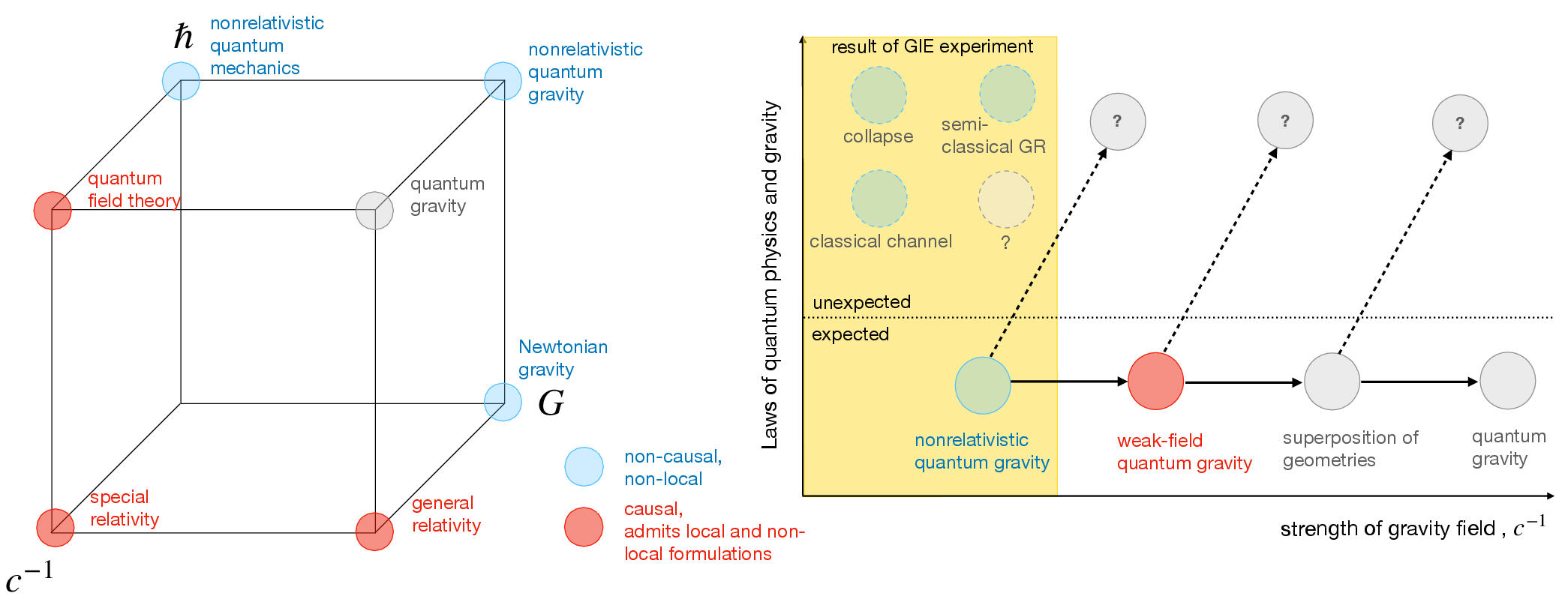
On inference of quantization from gravitationally induced entanglement (2206.00558v2)

Abstract: Observable signatures of the quantum nature of gravity at low energies have recently emerged as a promising new research field. One prominent avenue is to test for gravitationally induced entanglement between two mesoscopic masses prepared in spatial superposition. Here we analyze such proposals and what one can infer from them about the quantum nature of gravity, as well as the electromagnetic analogues of such tests. We show that it is not possible to draw conclusions about mediators: even within relativistic physics, entanglement generation can equally be described in terms of mediators or in terms of non-local processes -- relativity does not dictate a local channel. Such indirect tests therefore have limited ability to probe the nature of the process establishing the entanglement as their interpretation is inherently ambiguous. We also show that cosmological observations already demonstrate some aspects of quantization that these proposals aim to test. Nevertheless, the proposed experiments would probe how gravity is sourced by spatial superpositions of matter, an untested new regime of quantum physics.

• The paper demonstrates that gravitationally induced entanglement arises from non-relativistic quantum mechanics, challenging definitive proof of graviton quantization.
• It compares local mediator roles in the Lorentz gauge with non-local Coulomb gauge formulations, highlighting key methodological differences.
• The study implies that while GIE experiments confirm quantum features of Newtonian potentials, they do not decisively establish graviton mediation.

On Inference of Quantization from Gravitationally Induced Entanglement

Introduction

The paper of quantum gravity seeks to reconcile quantum mechanics with general relativity. A promising avenue is gravitationally induced entanglement (GIE), which involves testing gravitational fields' quantum nature through two masses prepared in spatial superposition. The interaction of these masses via a Newtonian gravitational potential might entangle their quantum states, supposedly hinting at quantum gravity. This essay investigates whether such experiments unambiguously indicate quantum gravity, or more specifically, the existence of gravitons as mediators, and examines analogous tests in electromagnetism.

Non-relativistic Quantum Mechanics

In quantum mechanics, the gravitational potential can be expressed as an operator owing to the quantized nature of its sources, such as masses in superposition. For two interacting particles, the Hamiltonian includes their kinetic and potential energy terms. However, given this setup, conclusions regarding mediators' nature remain elusive; gravitons do not manifest in this framework. Consequently, this non-relativistic limit suffices to predict GIE proposals, highlighting the inherently non-local nature of Newtonian interactions.

Electromagnetic Field Propositions

Local Mediators in Lorentz Gauge:

In QED's Lorentz gauge, all components of the electromagnetic field are quantized, localizing the interaction Lagrangian. The presence of scalar and longitudinal "virtual" photons here facilitates entanglement yet is unobservable directly. These mediators are responsible for local interaction, meaning entanglement and local operations demand that these auxiliary fields are quantized.

Figure 1: Schematic of an experimental setup to test for gravitationally induced entanglement.

Non-locality in Coulomb Gauge:

In contrast, Coulomb gauge formulations highlight non-local entanglement generation, bypassing mediators. The interaction Hamiltonian involves merely the Coulomb potential, emphasizing direct entanglement without traversing quantized fields. This renders LOCC arguments ineffectual for proving quantized mediators, revealing that the locality requirement isn't strictly necessary for entanglement given relativistic causality.

QED as Absorber Theory:

For further ambiguity resolution, considering absorber formulations such as Wheeler-Feynman's, where interactions have non-local character without fields, aligns with QED predictions. Indirect inferences from LOCC fail here, and the gravitational analogue faces similar issues.

Weak-field Quantum Gravity

Local Mediators in Lorentz Gauge:

In gravity's weak-field limit, quantum gravity parallels electromagnetic methods, with auxiliaries arising in Lorentz gauge quantization. Although auxiliary gravitons mediate entanglement, they, too, elude direct observation, echoing QED's dynamics without assuring graviton quantization.

Non-local Alternatives and Absorber Theories:

Poisson gauge formulations of gravity underscore non-local entanglement minus quantized mediators' necessity. Coupled with potential gravitational absorber theories in weak fields, these show further ambiguity in any definite quantization conclusion. However, this framework currently lacks a non-perturbative general relativity form.

Implications of GIE Experiments

The inferences from GIE tests are mainly ambiguous due to alternative theoretical formulations. Directly, successful GIE probes show masses in superposition source Newtonian fields, allowing further conclusions contingent on prior theoretical suppositions. Pre-existing cosmological evidence already points toward the quantum nature of gravity in similar contexts.

Figure 2: Left: Bronstein cube organizing various theories based on dependence on $\hbar, G$, and $c$.

Conclusion

GIE experiments, while revolutionary in potentially capturing quantum gravitational phenomenon, offer limited insights beyond proving the quantum mechanical nature of Newtonian potentials sourced by superposed masses. Graviton quantization is not verifiable without presuming specific local interactions, as alternatives exist for non-local processes consistent with known physics and current cosmological understandings. Thus, even successful GIE results might inform existing assumptions more than unearth novel explanations or affirm the quantization of gravitational interactions definitively.