Today's Experiments Suffice to Verify the Quantum Essence of Gravity (2508.03052v1)

Abstract: The gravity-mediated entanglement experiments employ concepts from quantum information to argue that if gravitational interaction creates entanglement between two systems, then gravity cannot be described by a classical system. However, the proposed experiments remain beyond out current technological capability, with optimistic projections placing the experiment outside of short-term future. Here we leverage quantum information techniques to argue that current matter-wave interferometers are sufficient to indirectly prove that gravitational interaction creates entanglement between two systems. Specifically, we prove that if we experimentally verify the Schr\"{o}dinger equation for a single delocalized system interacting gravitationally with an external mass, then the time evolution of two delocalized systems will lead to gravity-mediated entanglement. Our findings indicate that the experimental verification of the quantum essence of gravity is on the horizon.

• The paper demonstrates that matter-wave interferometry can test gravitationally induced entanglement as evidence of gravity’s quantum nature.
• The study employs Choi matrices and semidefinite programming to numerically validate that interactions follow the Schrödinger equation, leading to entanglement.
• The proposed experiments leverage current technology to measure phase shifts in mesoscopic masses, supporting the theory of quantum gravity.

Detailed Summary of "Today's Experiments Suffice to Verify the Quantum Essence of Gravity"

Introduction

The paper explores the viability of using current experimental techniques to validate the quantum essence of gravity, traditionally argued to be unachievable with present technology. It investigates whether gravity-mediated entanglement experiments can indirectly confirm gravitational interactions' quantum nature.

Quantum Information Framework

Building on quantum information, the paper uses the concepts of entanglement to argue that gravitational interactions cannot be purely classical systems if they facilitate entanglement between systems. Prior analyses suggested these experiments were technologically unfeasible in the short term. The paper counters this by suggesting that matter-wave interferometers, which can now delocalize quantum systems over considerable distances, are capable of indirectly proving gravity-induced entanglement through experimental validation of the Schrödinger equation in specific setups.

Methodology and Experimental Design

The argument leverages matter-wave interferometry to test the Schrödinger equation's validity for a delocalized system interacting gravitationally with a mass. The experiment involves mesoscopic masses held in superpositions, where gravitational phase shifts between interferometer arms relate to quantum effects rather than classical. The setup involves verifying that the interaction Hamiltonian for one delocalized and one localized system aligns with the Schrödinger equation, implying that gravity-induced entanglement would arise in systems where both are delocalized.

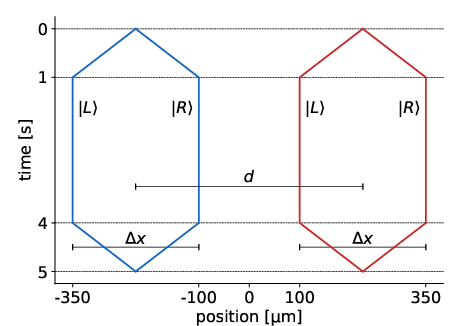
Figure 1: A spacetime diagram illustrating two mass interferometers separated by distance $d = 450 \mu m$, prompting gravitationally induced phase shifts.

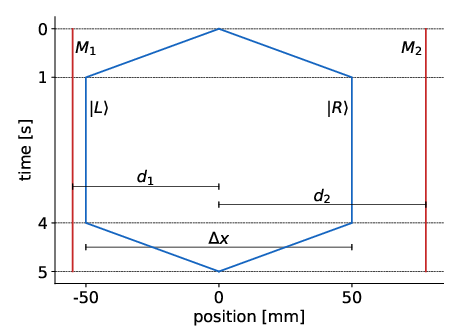
Figure 2: An interferometer experiment with a mass and localized systems to verify the Schrödinger equation's applicability beyond classical limits.

Proof of Quantum Behavior

The paper provides a rigorous mathematical framework to describe these systems, using Choi matrices to assert that if single systems conform to the Schrödinger equation, so too must dual delocalized systems, thus manifesting entanglement. A numerical counterpart, employing semidefinite programming, confirms that any positive time evolution satisfying the Schrödinger condition for individual systems results in entangled states for two interacting delocalized systems.

Numerical Validation

Numerical methods, alongside random initial state sampling, ensure that positive channels align with the Schrödinger prediction for individual systems, consequently establishing gravity-induced entanglement. Experiments incorporate validated quantum information techniques to ensure robust results within resource constraints.

Assumptions and Verification

Addressing experimental constraints, the paper acknowledges the impracticality of preparing extensive masses in superposition. It assumes mass equivalence in gravitational influence across microscopic and macroscopic levels. Experiments proposed measure gravitational fields of smaller systems without discrepancy, and suggestions for practical verification are given.

Conclusion

The research suggests that current technology suffices to indirectly verify key aspects of quantum gravity, emphasizing the quantum nature of gravity and corresponding entanglement implications. Future work should focus on theoretical refinements and clarifying gravity-mediated entanglement implications in the quantum field.

By leveraging quantum information principles with experimental modernity, the paper provides a compelling pathway to identifying gravity as inherently quantum, with significant implications for future exploration and understanding in quantum mechanics and relativity.