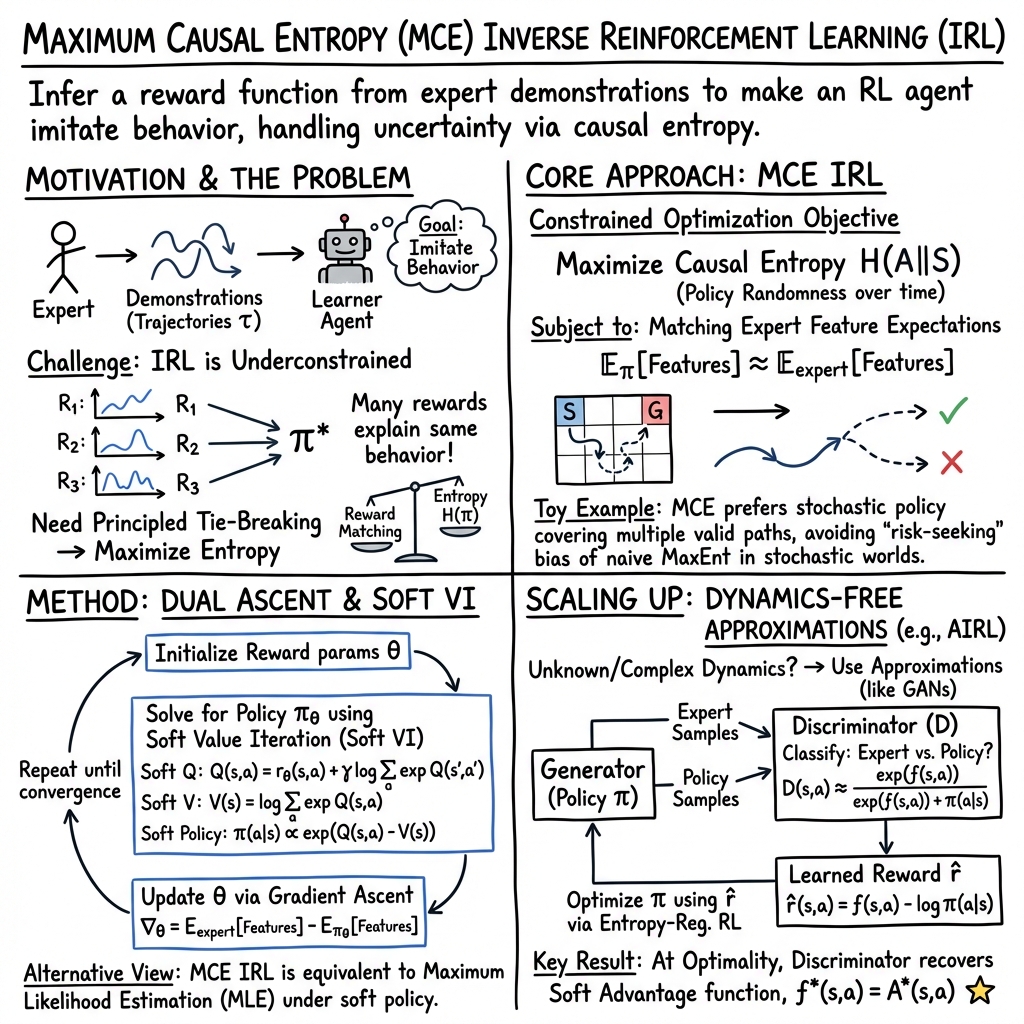
- The paper introduces Maximum Causal Entropy IRL by integrating entropy maximization to robustly infer reward functions from expert demonstrations.
- It formulates the problem using feature expectation matching and dual optimization to manage uncertainties from suboptimal actions.
- The study discusses extensions like Guided Cost Learning and AIRL, highlighting their scalability for high-dimensional and complex environments.
A Primer on Maximum Causal Entropy Inverse Reinforcement Learning
Introduction
The paper "A Primer on Maximum Causal Entropy Inverse Reinforcement Learning" (2203.11409) offers a comprehensive tutorial on Maximum Causal Entropy Inverse Reinforcement Learning (MCE IRL), an influential framework within the broader context of IRL. IRL techniques derive reward functions from expert demonstrations, effectively allowing machines to infer the desired behavior based on observed actions. MCE IRL stands out due to its ability to model the uncertainty inherent in human decision-making through the incorporation of entropy maximization, thereby providing a robust framework for handling suboptimal demonstrations.
Background on MCE IRL
Inverse Reinforcement Learning involves inferring the reward function from expert trajectories when explicit specification of such a function is infeasible or complex. MCE IRL enhances this process by adopting principles from information theory to introduce entropy into the learned policy. This approach helps manage the ambiguity stemming from multiple reward functions being consistent with the observed behavior and allows the policy to account for occasional suboptimal actions as random variations.
At the core is the idea of using causal entropy to model the observer's probability distribution over actions, considering not just the current state but the causality inherent in their sequence. This contrasts with other methods like Bayesian IRL, which aims to estimate a posterior distribution over possible reward functions but faces scalability challenges in complex environments.
The formulation of MCE IRL involves several key components:
Markov Decision Process
MCE IRL operates on Markov Decision Processes (MDPs) where the reward function is initially unknown. The system operates under the assumption that either the discount factor is less than one or the horizon is finite, allowing for stable return calculations.
Feature Expectation Matching
MCE IRL's primal problem seeks to match feature expectations between the learned policy and the expert behavior while maximizing causal entropy:
- Objective: Maximize causal entropy conditioned on ensuring feature expectations align with those of the expert.
- Lagrangian: Incorporate the feature expectation constraints into a Lagrangian framework to transform the constraint optimization into a more tractable form.
- Dual Problem: Insight is gained by translating the optimization into a dual problem which focuses on reward weights, thus simplifying the optimization by concentrating on reward parameter estimation.
Maximum Likelihood Perspective
Beyond feature matching, the paper elaborates on interpreting MCE IRL as a problem of Maximum Likelihood Estimation (MLE). This perspective enables the adaptation of non-linear reward structures within the IRL framework, expanding its applicability and allowing it to handle more intricate modeling scenarios beyond linear reward functions.
Key Algorithms: GCL and AIRL
Two prominent extensions are highlighted in the paper: Guided Cost Learning (GCL) and Adversarial IRL (AIRL). Both aim to scale IRL methods to high-dimensional environments by bypassing the need for a known model of the environment's dynamics, crucial for practical applications in real-world scenarios.
Guided Cost Learning
As a method that leverages importance sampling, GCL adapts as new data is acquired, dynamically adjusting the policy representation to closely mimic the learned rewards, ensuring efficient IRL application in complex settings.
Adversarial IRL
AIRL, drawing inspiration from Generative Adversarial Networks (GANs), uses a discriminative approach to distinguish between expert and learned trajectories, refining the reward functions iteratively to better capture the underlying behavioral patterns of the expert demonstrations. This approach allows AIRL to effectively handle continuous state and action spaces, making it amenable to tasks like robotic control and autonomous driving.
Practical and Theoretical Implications
MCE IRL and its derivatives have profound implications for artificial intelligence, especially in areas requiring nuanced human-like decision-making. These techniques unearth latent reward structures that machines can exploit, thus aligning more closely with human intent and facilitating greater autonomy and adaptability in AI systems.
Future developments may focus on refining these models to handle stochastic environments with higher fidelity or simplifying computation without sacrificing the richness of the inferred policies. The exploration of causal structures and entropy-based frameworks also opens avenues for integrating these approaches with other learning paradigms, enhancing their robustness and applicability across diverse domains.
Conclusion
The paper is an authoritative guide on Maximum Causal Entropy IRL with extensive exploration of its derivation, formulation, and practical extensions in machine learning. By grounding the IRL approach in entropy maximization, it provides a principled way to handle uncertainty and suboptimal demonstrations, paving the path for more intelligent, adaptive systems that can seamlessly mimic human-like behaviors in complex environments.