Kernel Based Maximum Entropy Inverse Reinforcement Learning for Mean-Field Games

Abstract: We consider the maximum causal entropy inverse reinforcement learning problem for infinite-horizon stationary mean-field games, in which we model the unknown reward function within a reproducing kernel Hilbert space. This allows the inference of rich and potentially nonlinear reward structures directly from expert demonstrations, in contrast to most existing inverse reinforcement learning approaches for mean-field games that typically restrict the reward function to a linear combination of a fixed finite set of basis functions. We also focus on the infinite-horizon cost structure, whereas prior studies primarily rely on finite-horizon formulations. We introduce a Lagrangian relaxation to this maximum causal entropy inverse reinforcement learning problem that enables us to reformulate it as an unconstrained log-likelihood maximization problem, and obtain a solution \lk{via} a gradient ascent algorithm. To illustrate the theoretical consistency of the algorithm, we establish the smoothness of the log-likelihood objective by proving the Fréchet differentiability of the related soft Bellman operators with respect to the parameters in the reproducing kernel Hilbert space. We demonstrate the effectiveness of our method on a mean-field traffic routing game, where it accurately recovers expert behavior.

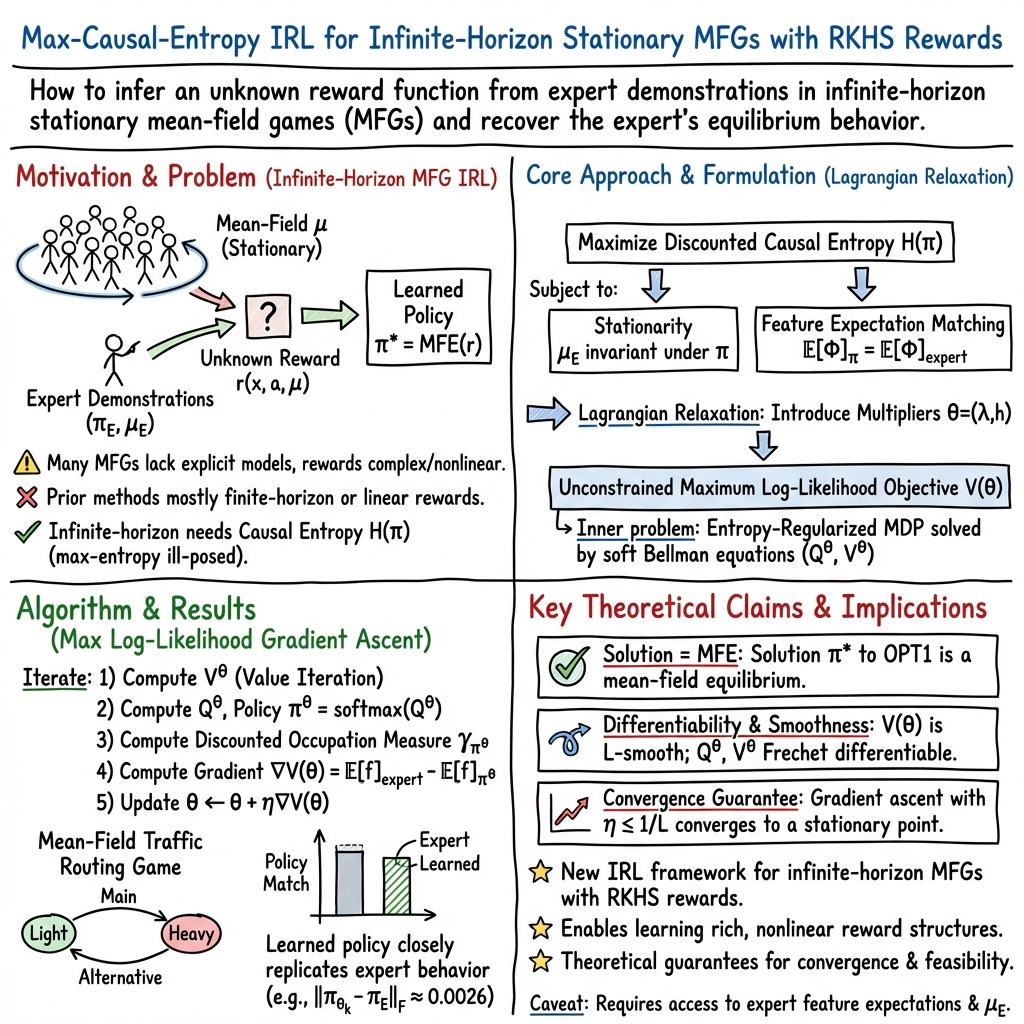
• The paper proposes a novel kernel-based maximum entropy inverse reinforcement learning framework that models complex, nonlinear reward functions in infinite-horizon mean-field games.
• It employs reproducing kernel Hilbert space and gradient ascent techniques, demonstrating theoretical consistency through smooth Frechet differentiability of soft Bellman operators.
• Numerical validation with a mean-field traffic routing game confirms the method's ability to accurately recover expert policies and ensures convergence of the gradient ascent algorithm.

Kernel Based Maximum Entropy Inverse Reinforcement Learning for Mean-Field Games

Introduction

The paper "Kernel Based Maximum Entropy Inverse Reinforcement Learning for Mean-Field Games" (2507.14529) presents an innovative approach to solving inverse reinforcement learning (IRL) challenges within the context of mean-field games (MFGs). In particular, this study addresses the IRL problem by proposing a method that directly models the unknown reward function in a reproducing kernel Hilbert space (RKHS). This approach offers a departure from traditional methodologies that often restrict the reward function to linear combinations of a finite set of basis functions, thereby facilitating the inference of complex, nonlinear reward structures from expert demonstrations.

Theoretical Framework

The authors focus on infinite-horizon stationary MFGs, extending current frameworks which predominantly operate under finite-horizon settings. Central to this approach is the use of maximum causal entropy to handle the inherent complexity and variability in expert demonstration data. This principle is adapted to the infinite-horizon context, circumventing the inapplicability of classical maximum entropy approaches by leveraging causality constraints, as previously developed for infinite-horizon MDPs by Zhang et al.

The methodology involves a Lagrangian relaxation that transforms the problem into an unconstrained log-likelihood maximization, subsequently addressed via a gradient ascent algorithm. The merit of this method is underscored by its theoretical consistency; specifically, the smoothness of the log-likelihood objective is established through the Frechet differentiability of associated soft Bellman operators with respect to RKHS parameters.

Numerical Validation

The practicality and efficacy of the proposed algorithm are demonstrated through a mean-field traffic routing game. Results indicate that the approach accurately recovers expert behavior, validating the theoretical claims of the study. A significant aspect of this validation is the establishment of the convergence of the gradient ascent algorithm, evidenced by the smoothness and differentiability of the involved Bellman operations.

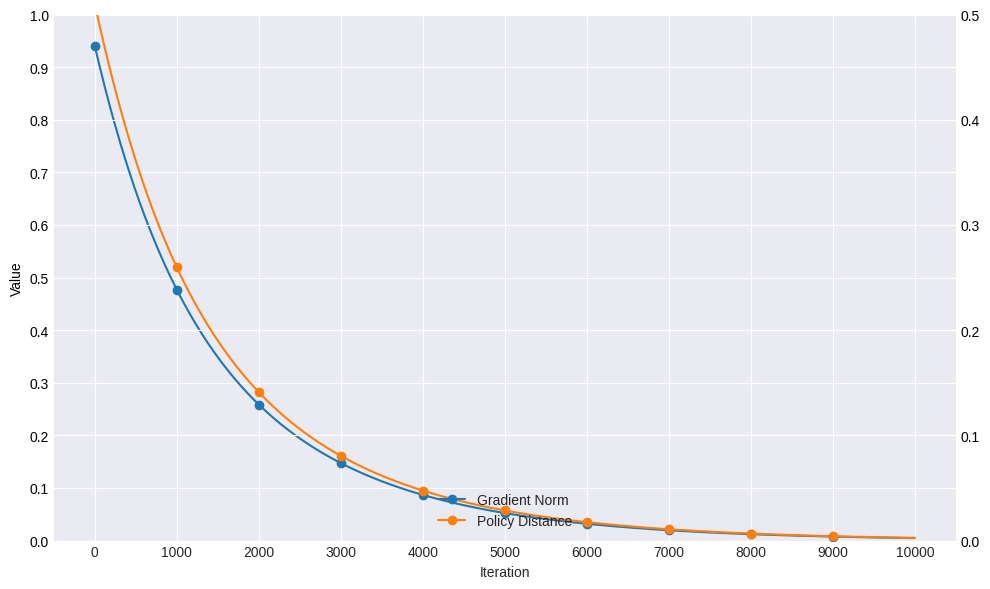
Figure 1: By the end of training, the $\ell_2$ norm of the gradient $\nabla \mathcal{V}(\theta_k)$ had converged to a value of 0.0047.

Implications and Future Directions

The implications of this research are multifaceted. Practically, it facilitates the derivation of sophisticated policies that mimic expert behaviors across complex systems without the need for explicit reward specifications. Theoretically, it pushes the boundaries of current IRL methodologies, expanding their applicability to infinite-horizon problems within MFGs. The use of RKHS to model rewards opens up fresh avenues for incorporating kernel methods into reinforcement learning frameworks, enhancing the adaptability and robustness of learning systems.

Future research could extend this framework to other types of games and decision-making environments. Moreover, applying this method to high-dimensional, real-world datasets presents a potential area for expansion, offering the possibility of uncovering insights in complex interactive systems.

Conclusion

In conclusion, this paper presents a significant advancement in the field of IRL by integrating kernel methods into the modeling of reward functions within the MFG framework. By addressing the limitations of existing approaches, it lays the groundwork for more robust and versatile applications in AI, particularly in environments characterized by large populations of interacting agents. The authors provide both a solid theoretical foundation and compelling practical validation, indicating promising avenues for future exploration and application.