EP-PINNs: Cardiac Electrophysiology Characterisation using Physics-Informed Neural Networks (2112.07703v1)

Abstract: Accurately inferring underlying electrophysiological (EP) tissue properties from action potential recordings is expected to be clinically useful in the diagnosis and treatment of arrhythmias such as atrial fibrillation, but it is notoriously difficult to perform. We present EP-PINNs (Physics-Informed Neural Networks), a novel tool for accurate action potential simulation and EP parameter estimation, from sparse amounts of EP data. We demonstrate, using 1D and 2D in silico data, how EP-PINNs are able to reconstruct the spatio-temporal evolution of action potentials, whilst predicting parameters related to action potential duration (APD), excitability and diffusion coefficients. EP-PINNs are additionally able to identify heterogeneities in EP properties, making them potentially useful for the detection of fibrosis and other localised pathology linked to arrhythmias. Finally, we show EP-PINNs effectiveness on biological in vitro preparations, by characterising the effect of anti-arrhythmic drugs on APD using optical mapping data. EP-PINNs are a promising clinical tool for the characterisation and potential treatment guidance of arrhythmias.

• The paper introduces EP-PINNs which combines the Aliev-Panfilov model with PINNs to accurately infer cardiac EP parameters such as APD and diffusion coefficients.
• It employs a hybrid loss function that balances noisy experimental data with biophysical equations, ensuring robust forward and inverse modeling performance.
• EP-PINNs is validated on both simulated and real optical mapping data, highlighting its potential for improved diagnosis and treatment of cardiac arrhythmias.

EP-PINNs: Cardiac Electrophysiology Characterisation using Physics-Informed Neural Networks

The paper discusses EP-PINNs, a framework utilizing Physics-Informed Neural Networks (PINNs) to estimate cardiac electrophysiology (EP) parameters from sparse measurements of transmembrane potentials. This work aims to enhance the diagnosis and treatment of arrhythmias by accurately inferring underlying tissue properties.

Introduction to EP-PINNs

EP-PINNs leverage the predictive capabilities of PINNs in cardiac EP, integrating biophysical models with machine learning to infer tissue properties from limited data. This method presents a novel approach for simulating cardiac action potentials and estimating key parameters such as the action potential duration (APD), excitability, and diffusion coefficients.

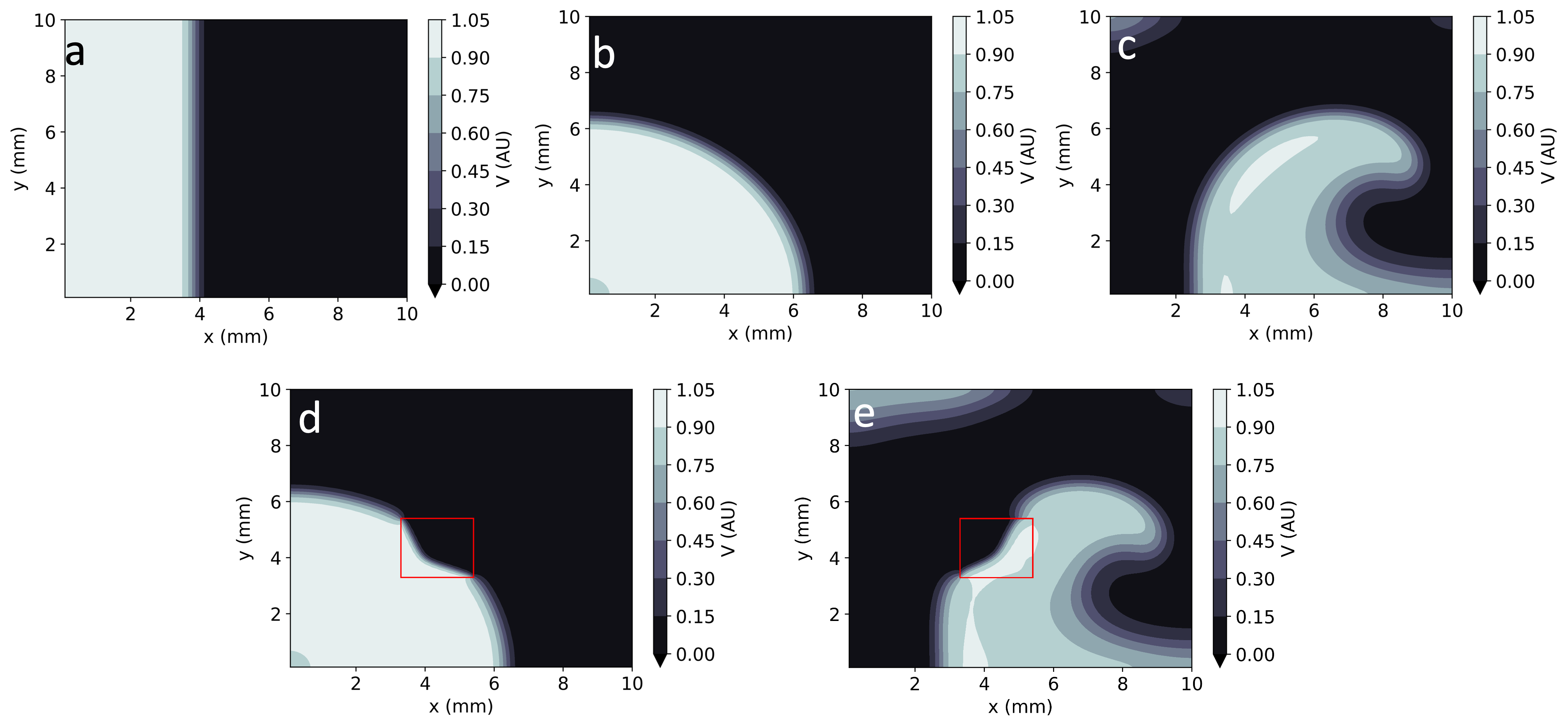
Figure 1: Numerical solutions to the Aliev-Panfilov monodomain system: planar, centrifugal, and spiral waves with and without heterogeneities.

Methodology

Biophysical Model and PINNs

The Aliev-Panfilov model, a two-variable representation of cardiac excitation, is utilized. It forms the basis for forward and inverse solutions using EP-PINNs. The model encompasses both PDEs for spatial potential distribution and ODEs for ionic fluxes, expressed through smooth, differentiable functions.

EP-PINNs incorporate these equations into their learning process, minimizing a hybrid loss function that combines agreement with experimental data and adherence to the governing physics.

Network Architecture

The EP-PINNs architecture, designed for flexibility, employs fully connected layers adjusted according to problem complexity. Two specific architectures are discussed: one for homogeneous scenarios and another more complex structure for spatially-varying parameters like the diffusion coefficient $D$.

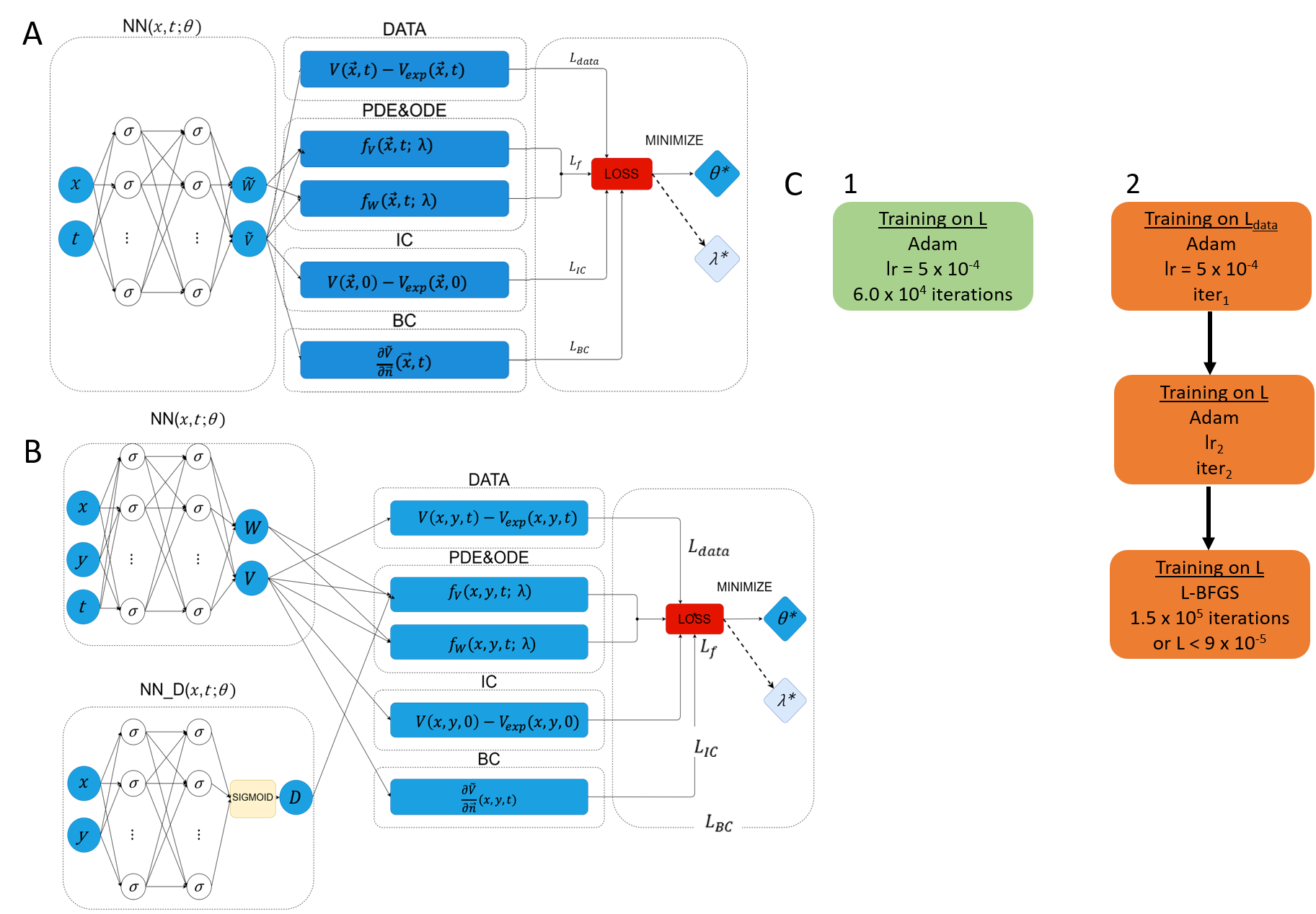
Figure 2: Network architectures and training schemes for EP-PINNs, differentiating between homogeneous and spatially varied conditions.

Results

Forward Modeling

EP-PINNs demonstrated robust performance in reproducing action potential propagation in both 1D and 2D domains under various wave conditions, including planar and spiral waves, even with data sparsity and noise.

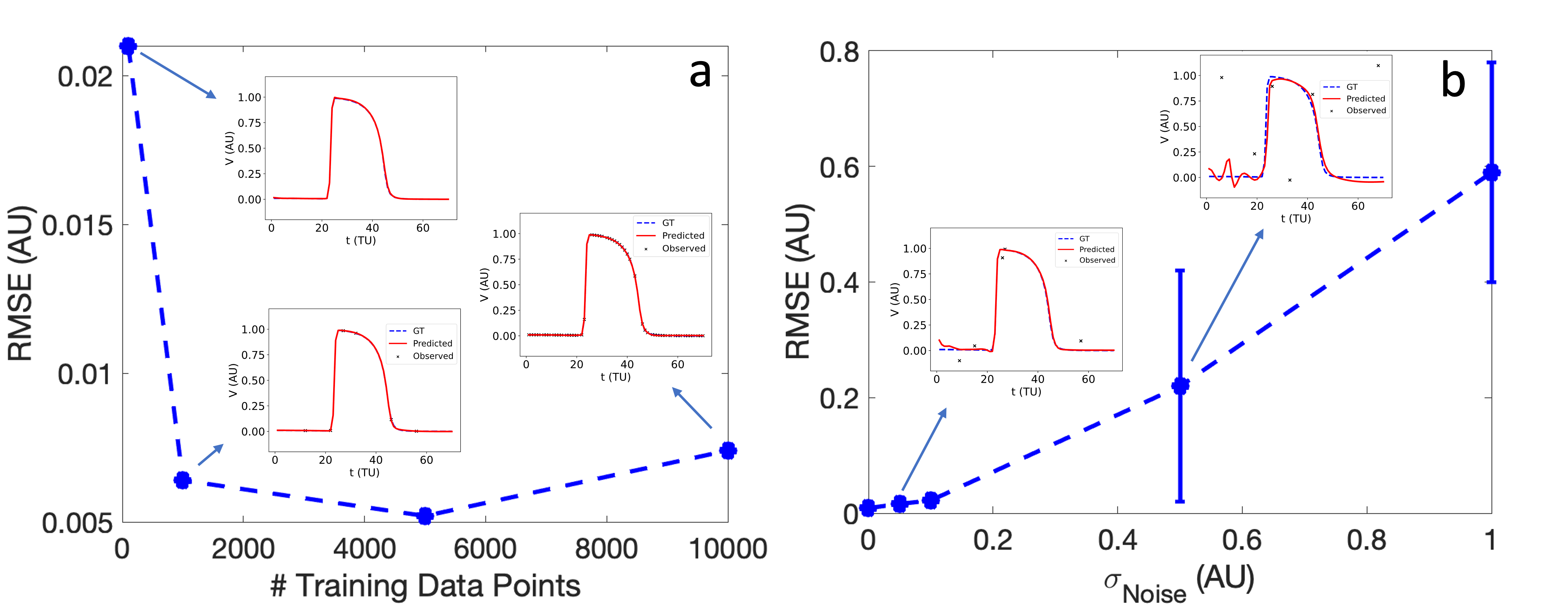
Figure 3: Impact of data sparsity and noise on EP-PINNs $V$ estimates, highlighting resistance to data quality issues.

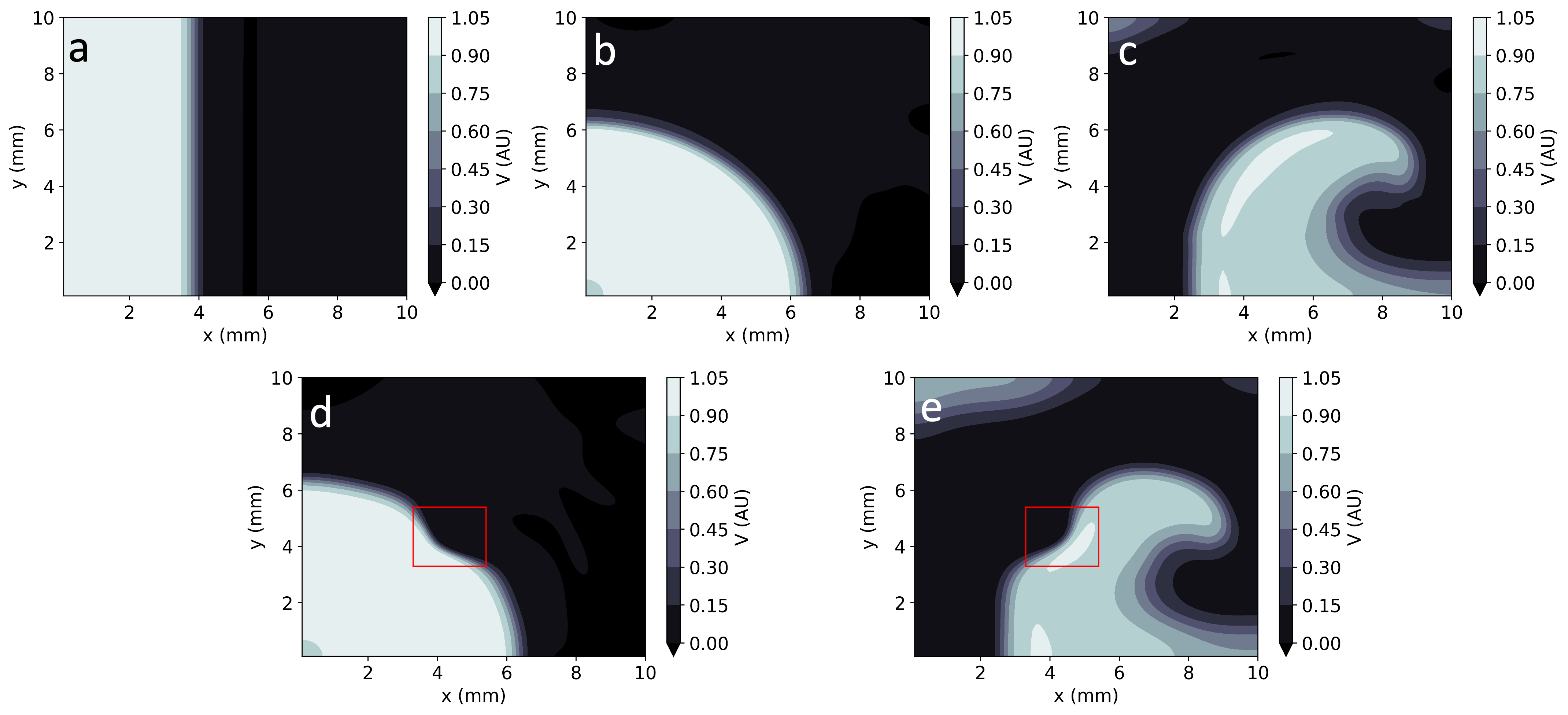
Figure 4: Comparison of EP-PINNs solutions in 2D with ground truth data, showcasing accuracy in different wave patterns.

Inverse Parameter Estimation

EP-PINNs effectively estimated global EP parameters under noisy conditions, showing stronger results for APD-related parameters. The method also accurately identified spatial heterogeneities, which are critical for localizing arrhythmic substrates.

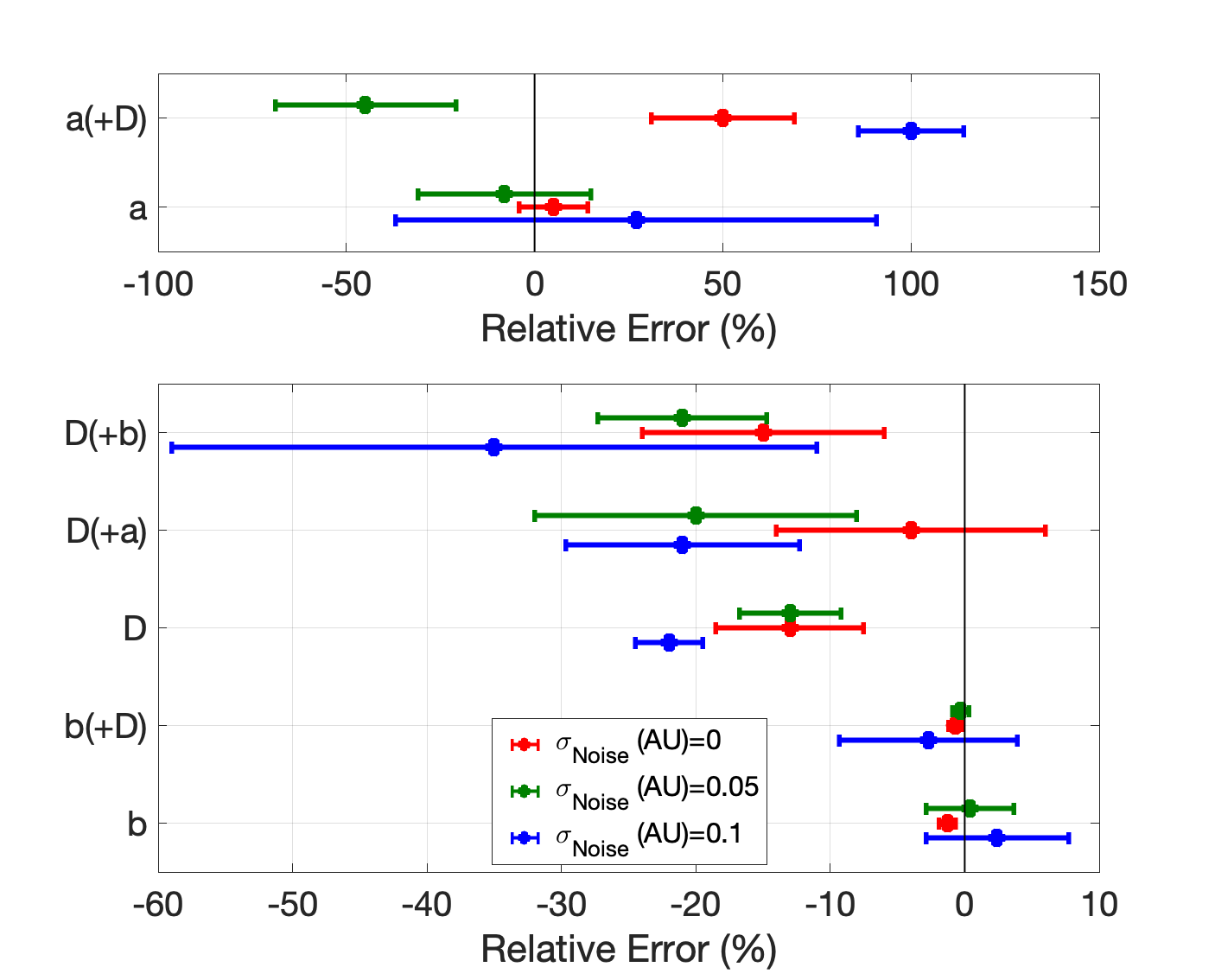
Figure 5: Error in parameter estimates under varying noise levels, indicating robustness in challenging conditions.

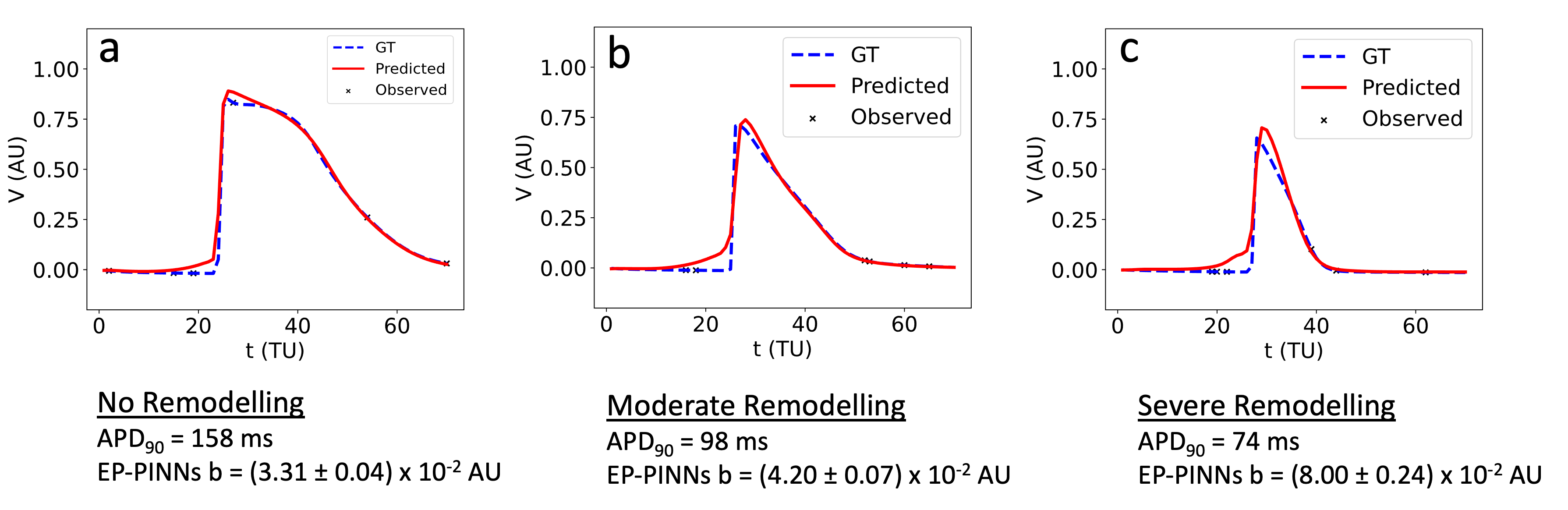
Figure 6: EP-PINNs estimation of AF-induced remodelling in a complex atrial model, showcasing adaptability beyond training conditions.

Real Data Application

The framework successfully extended to experimental optical mapping data, identifying pharmacological effects on APD. This capability underscores EP-PINNs potential in real-world clinical scenarios.

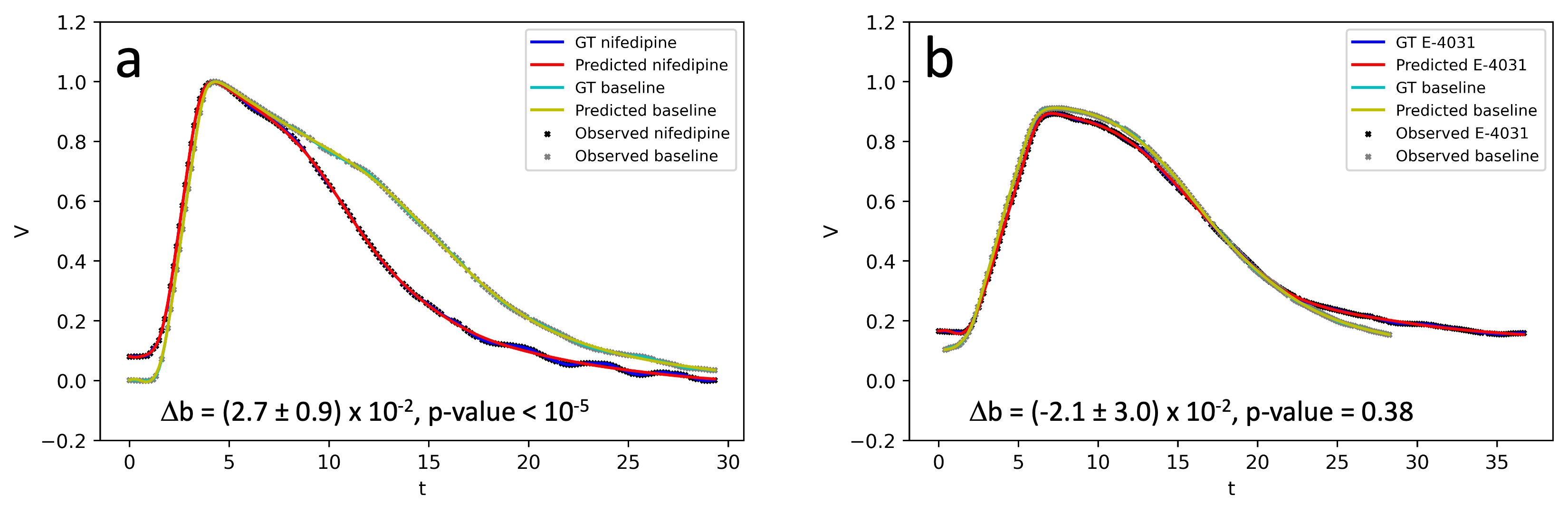
Figure 7: Estimation of pharmacological effects on APD from optical mapping data, validating EP-PINNs' experimental applicability.

Discussion

EP-PINNs offer a significant advancement in cardiac EP parameter estimation, efficiently inferring comprehensive EP characteristics from sparse datasets. This approach provides a promising tool for enhancing the precision of cardiac arrhythmia management. Future developments could involve simulating more complex models, extending to 3D cardiac structures, and integrating clinical measurements of extracellular potentials.

These developments would further bridge the gap between computational models and clinical practice, offering tailored therapeutic strategies based on patient-specific EP characterizations.

Conclusion

The research establishes EP-PINNs as a powerful method for cardiac EP simulation and parameter estimation. This framework has the potential to revolutionize the diagnosis and treatment guidance of cardiac arrhythmias, providing a more nuanced understanding of the underlying electrophysiological changes. Further exploration and enhancement of this technique could significantly impact personalized cardiology.