Conditional physics informed neural networks (2104.02741v1)

Abstract: We introduce conditional PINNs (physics informed neural networks) for estimating the solution of classes of eigenvalue problems. The concept of PINNs is expanded to learn not only the solution of one particular differential equation but the solutions to a class of problems. We demonstrate this idea by estimating the coercive field of permanent magnets which depends on the width and strength of local defects. When the neural network incorporates the physics of magnetization reversal, training can be achieved in an unsupervised way. There is no need to generate labeled training data. The presented test cases have been rigorously studied in the past. Thus, a detailed and easy comparison with analytical solutions is made. We show that a single deep neural network can learn the solution of partial differential equations for an entire class of problems.

• The paper introduces Conditional PINNs to extend traditional PINNs for efficiently solving parameterized eigenvalue problems by embedding physical laws into the loss function.
• It leverages tag vectors as conditional inputs to generalize solutions across a range of PDEs, including challenging micromagnetic models with varying defect parameters.
• The network’s performance is validated against classical solutions in both one-dimensional and three-dimensional settings, demonstrating robustness and enhanced accuracy in eigenfunction approximation.

Conditional Physics Informed Neural Networks: An Expert Overview

Introduction

Physics Informed Neural Networks (PINNs) are neural networks designed to solve partial differential equations (PDEs) by incorporating the physical laws governing these equations directly into the training process. Conditional PINNs introduce a novel enhancement by extending this concept to parameterized families of PDEs. This paper presents Conditional PINNs to efficiently solve classes of eigenvalue problems with applications in micromagnetics.

Neural Networks for Eigenvalue Problems

Conditional PINNs leverage the concept of embedding the physics of eigenvalue problems within the architecture of neural networks. By incorporating the physical constraints directly into the loss function, these networks eliminate the need for labeled data, thus enabling an unsupervised learning paradigm. The PINN architecture approximates both the eigenvalue and the eigenfunction, optimizing the weights through direct minimization of a physics-informed loss function derived from the PDEs.

The variational form of eigenvalue problems, such as the Sturm-Liouville problem, provides the basis for these calculations. In the one-dimensional scenario, the functional $I(y)$ is minimized subject to constraints, facilitating eigenvalue approximation and satisfying boundary conditions under the Ritz method framework. The penalty method is applied to handle constraints effectively, optimizing training through stochastic gradient descent and quasi-Monte Carlo methods.

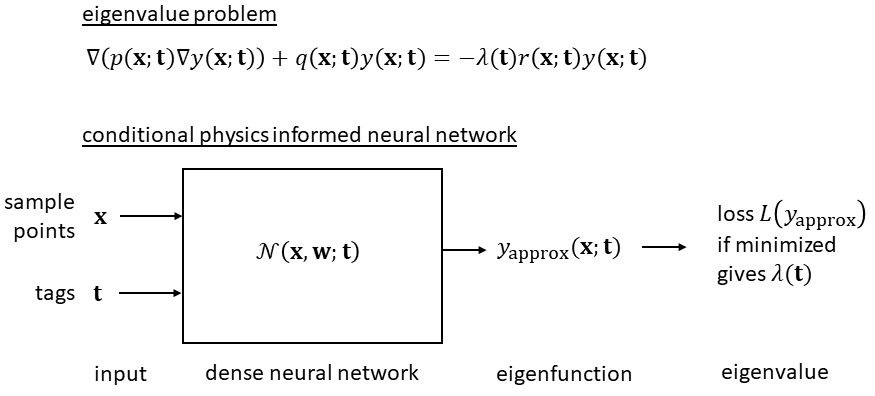
Figure 1: Overview of the Conditional PINN for solving classes of eigenvalue problems.

Learning Solutions for Classes of Problems

Distinctive to Conditional PINNs is their ability to generalize solutions across a range of parameterized problems. By using tag vectors as conditional inputs, the network is trained to handle variations in problem parameters, such as coefficients of eigenvalue equations, thereby offering a flexible solution strategy. The method precisely encodes solutions for multiple scenarios in micromagnetics, such as magnetic defects and inhomogeneous nucleation fields, making it adaptable to broader engineering challenges.

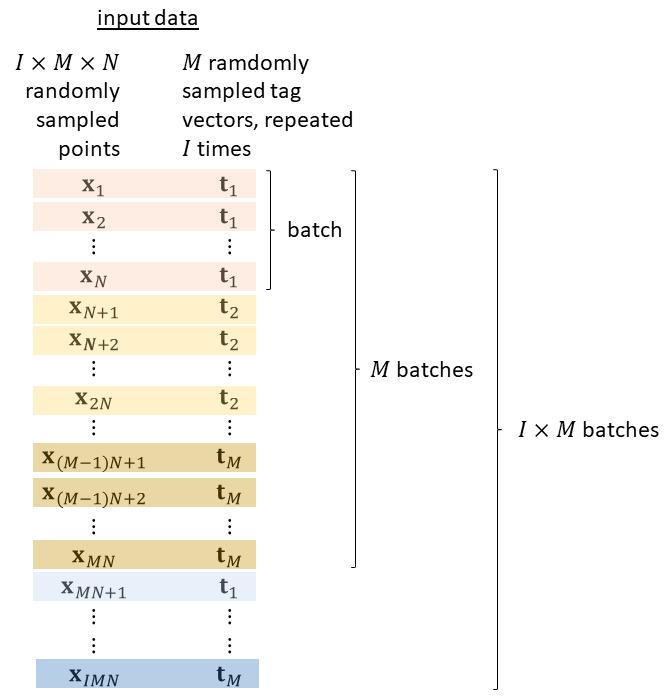
Figure 2: Input data configuration for Conditional PINNs, illustrating the separable roles of spatial sampling and parameter tags.

Results in Micromagnetic Applications

The implementation of Conditional PINNs in micromagnetics demonstrates their applicability. For instance, in one-dimensional micromagnetic modeling, the neural network successfully predicts nucleation fields in magnets with defects, validating the theoretical model against classical solutions and providing a detailed comparison of eigenfunctions for different parameter sets.

In three-dimensional problems encapsulating soft magnetic inclusions within hard magnetic matrices, the network efficiently predicts nucleation fields based on defect size, magnetization, and exchange constants. The results are benchmarked against known analytical solutions to quantify accuracy and validate the network's prediction capabilities.

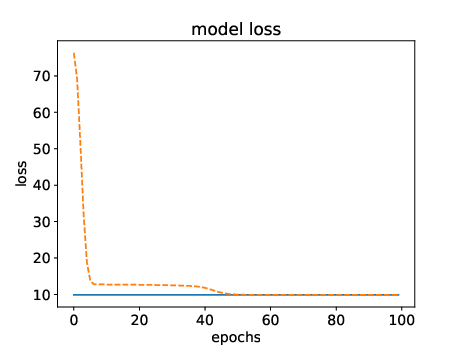
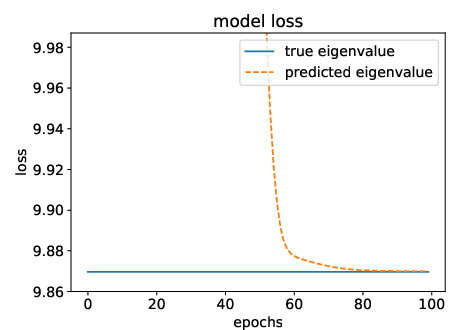
Figure 3: Approximated eigenvalue convergence over training epochs, showcasing improvement towards theoretical predictions.

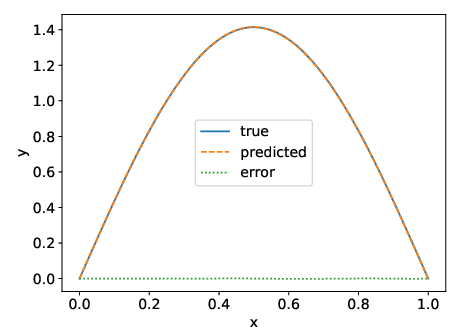
Figure 4: True versus approximated eigenfunction comparison for specific eigenvalue problems.

Conclusion

Conditional PINNs represent a significant advancement in solving parameter-dependent eigenvalue problems. They provide an unsupervised, physics-informed framework capable of spanning a class of PDEs, highlighting their utility in engineering applications like materials science and magnet design. As AI techniques continue to evolve, the potential for Conditional PINNs within other domains of scientific computing is substantial, opening avenues for rapid solution approximation and optimization in complex multi-parameter scenarios.