Dynamic Graph Convolutional Recurrent Network for Traffic Prediction: Benchmark and Solution

Abstract: Traffic prediction is the cornerstone of an intelligent transportation system. Accurate traffic forecasting is essential for the applications of smart cities, i.e., intelligent traffic management and urban planning. Although various methods are proposed for spatio-temporal modeling, they ignore the dynamic characteristics of correlations among locations on road networks. Meanwhile, most Recurrent Neural Network (RNN) based works are not efficient enough due to their recurrent operations. Additionally, there is a severe lack of fair comparison among different methods on the same datasets. To address the above challenges, in this paper, we propose a novel traffic prediction framework, named Dynamic Graph Convolutional Recurrent Network (DGCRN). In DGCRN, hyper-networks are designed to leverage and extract dynamic characteristics from node attributes, while the parameters of dynamic filters are generated at each time step. We filter the node embeddings and then use them to generate a dynamic graph, which is integrated with a pre-defined static graph. As far as we know, we are the first to employ a generation method to model fine topology of dynamic graph at each time step. Further, to enhance efficiency and performance, we employ a training strategy for DGCRN by restricting the iteration number of decoder during forward and backward propagation. Finally, a reproducible standardized benchmark and a brand new representative traffic dataset are opened for fair comparison and further research. Extensive experiments on three datasets demonstrate that our model outperforms 15 baselines consistently.

• The paper introduces DGCRN, which dynamically generates graph structures through recurrent networks to model spatio-temporal traffic patterns.
• It employs a hybrid approach integrating dynamic and static adjacency matrices to capture evolving road network correlations.
• Experimental results on METR-LA, PEMS-BAY, and NE-BJ datasets demonstrate state-of-the-art performance and establish a reproducible benchmarking framework.

Dynamic Graph Convolutional Recurrent Network for Traffic Prediction: Benchmark and Solution

Traffic prediction stands as a pivotal element within intelligent transportation systems, aiming to optimize urban planning and traffic management by forecasting future traffic conditions. Despite the numerous approaches developed for spatio-temporal modeling, these methods often overlook the dynamic attributes inherent to correlations among locations within a road network. Moreover, recurrent neural network-based methods typically suffer from inefficiencies due to recurrent operations, and there is a notable absence of comprehensive comparisons among different methodologies across identical datasets. This paper introduces the Dynamic Graph Convolutional Recurrent Network (DGCRN), a novel framework designed to address these challenges by generating dynamic graph structures in tandem with recurrent operations, thus modeling fine-grained and iterative topologies. DGCRN also serves as the basis for a reproducible traffic prediction benchmark, incorporating a new dataset to facilitate fair comparisons.

Methodology

Dynamic Graph Convolutional Recurrent Network (DGCRN)

DGCRN is structured around a sequence-to-sequence architecture, incorporating an encoder and a decoder. Central to its performance is the generation of dynamic adjacency matrices at each time step, integrating both static and dynamic graphs within the graph convolution module. This methodology effectively captures and models the dynamic and nonlinear spatio-temporal correlations required for precise traffic forecasting.

Figure 1: The architecture of DGCRN.

Graph Generator

DGCRN employs a hyper-network to iteratively generate dynamic adjacency matrices, capturing dynamic characteristics at each time step. Dynamic node embeddings are computed using the dynamic filters generated by the hyper-network, which incorporate historical data and current node attributes. This step-wise dynamic graph generation, synchronized with RNN operations, enhances message-passing processes and spatial dependency modeling.

Dynamic Graph Convolutional Recurrent Module

The module integrates dynamic and static adjacency matrices to perform dynamic graph convolutions. This hybrid approach captures both static road distances and dynamic node attributes, enabling efficient and accurate modeling of spatio-temporal dependencies. The dynamically generated graphs enrich traditional GRU operations within the DGCRM, optimizing sequential and spatial correlation management.

Figure 2: Structure of dynamic graph convolution module.

Training Strategy

To address the inefficiencies inherent in RNN architectures, a curriculum learning strategy is implemented. This technique restricts the training process to shorter sequences initially, gradually extending to full sequence lengths. This method improves training speed and memory efficiency while enhancing model performance through reinforced short-range prediction capabilities.

Figure 3: Efficiency of curriculum learning.

Experimental Evaluation

Benchmark Results

DGCRN demonstrates state-of-the-art performance across METR-LA, PEMS-BAY, and NE-BJ datasets, outperforming 15 baseline models. The dynamic graph generation contributes substantially to metric improvements, particularly within complex traffic conditions as observed in the NE-BJ dataset.

Figure 4: Road segment distribution of the NE-BJ dataset.

Ablation and Parameter Studies

Comprehensive ablation studies confirm the critical role of dynamic graph constructions, demonstrating that excluding dynamic components results in diminished model efficacy. Parameter studies further show optimal configurations for node embeddings, hidden states, and decay steps in scheduled sampling, adapting to dataset-specific requirements.

Figure 5: Distributions of inter-node correlations and speed on PEMS-BAY, METR-LA and NE-BJ datasets.

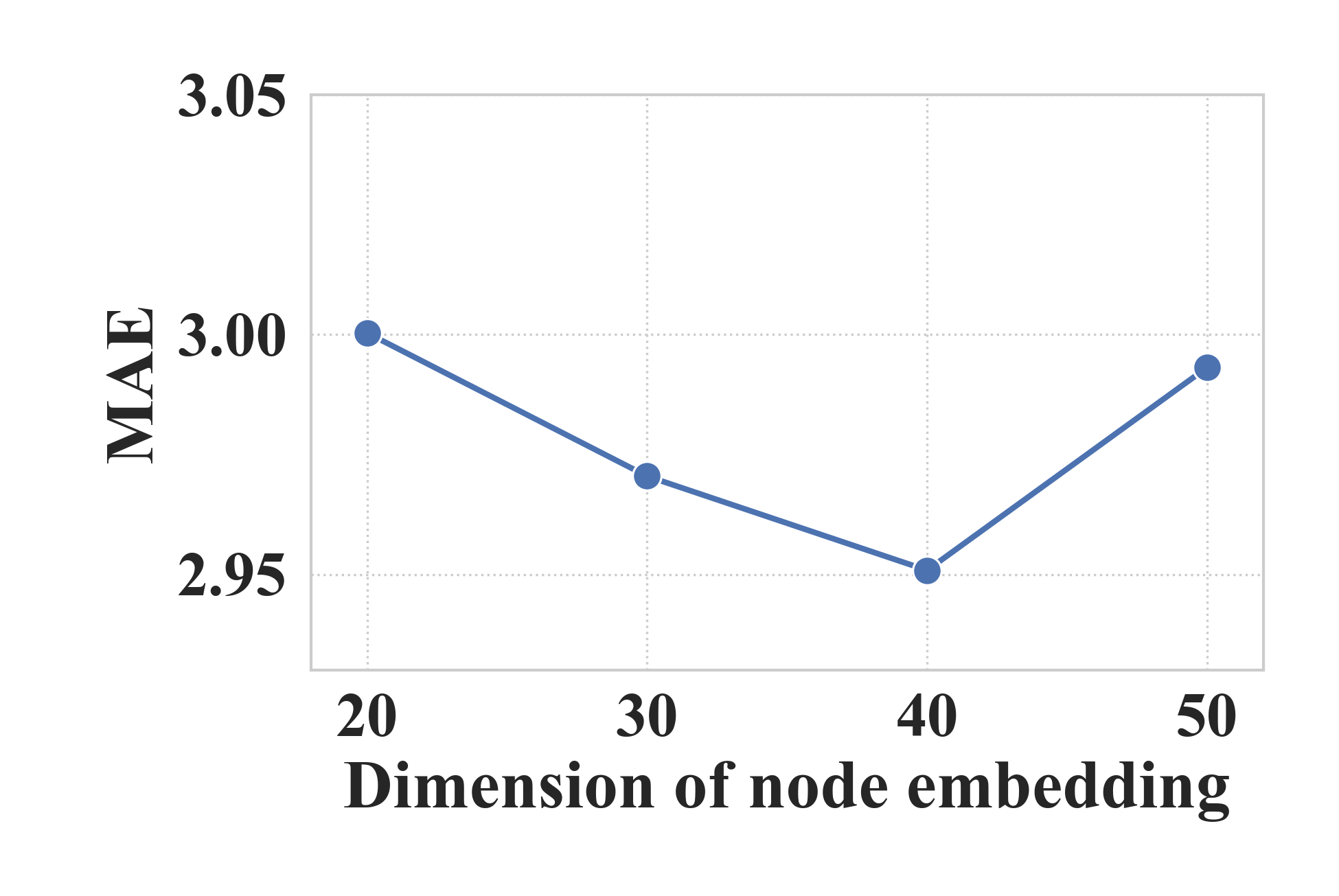
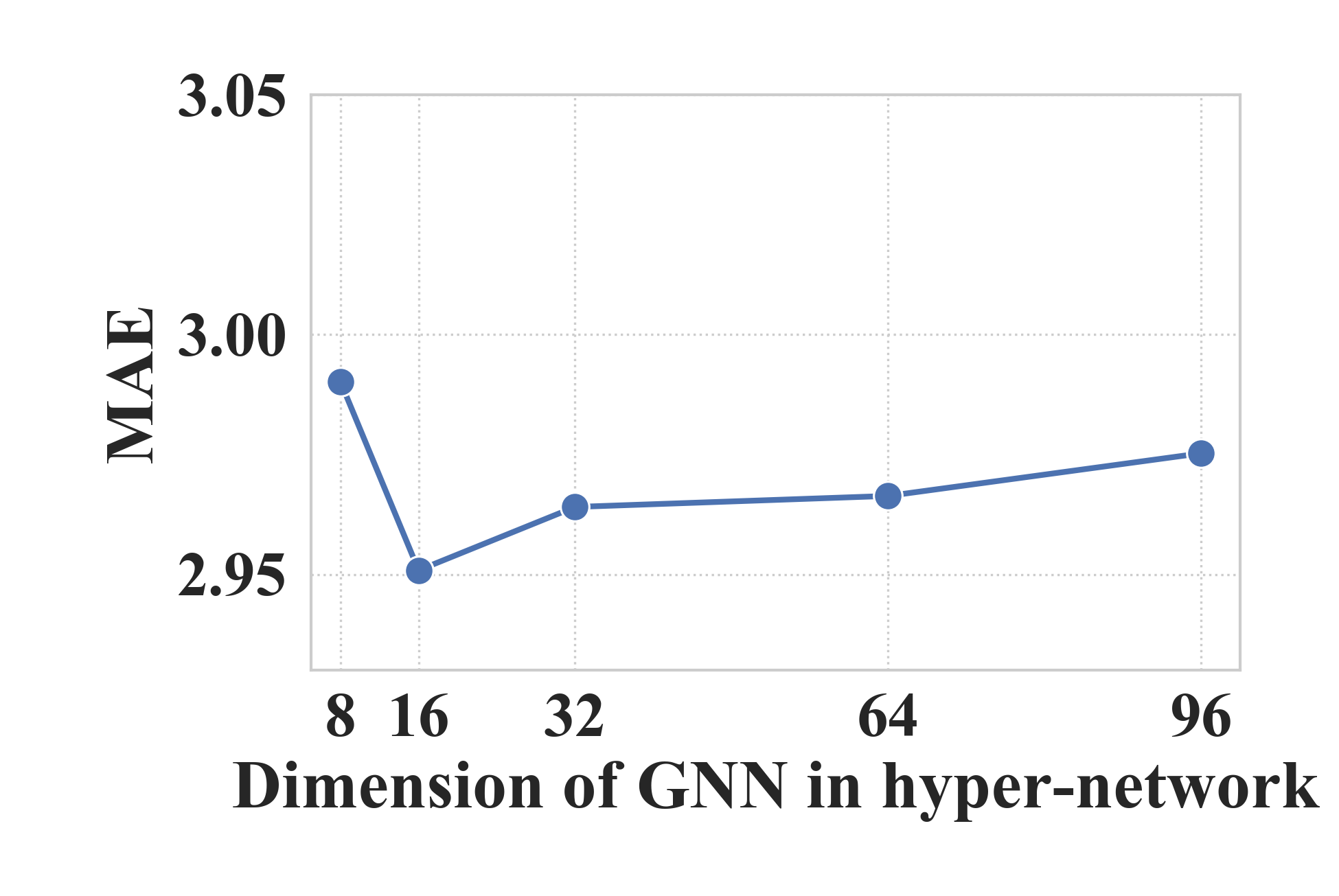
Figure 6: Parameter Study on METR-LA.

Conclusion

The introduction of step-wise dynamic graph generation offers promising advancements in traffic prediction, capturing dynamic spatio-temporal correlations that static graphs fail to model effectively. The DGCRN framework not only enhances predictive accuracy but also provides a robust benchmark for evaluating traffic prediction models. Future work will explore the integration of diverse external factors, expanding the dynamic model's adaptability to varying urban environments.