- The paper reveals that covariate shift arises in three regimes—Easy, Goldilocks, and Hard—each affecting imitation learning performance differently.
- The paper introduces ALICE, an algorithm that uses density ratio reweighting and cached expert demonstrations to correct feedback-induced errors.
- The paper calls for new benchmark environments that better simulate real-world decision-making challenges in imitation learning.
Feedback in Imitation Learning: Covariate Shift Regimes
Introduction
The paper discusses the challenges imitation learning faces due to feedback-induced covariate shifts, particularly in the context of decision making where previous actions influence future inputs. This work identifies three distinct regimes of covariate shift—Easy, Goldilocks, and Hard—each characterized by different levels of problem complexity and model specifications. The primary focus is on understanding and mitigating these shifts to improve imitation learning performance in practical settings.
Covariate Shift in Imitation Learning
Imitation learning (IL) involves learning policies by mimicking expert demonstrations, often suffering from covariate shifts due to feedback loops. Traditional behavior cloning (BC) is plagued by errors from training in controlled environments that do not surface until real-world application. These errors can compound over time, leading to a significant gap between training and execution performance (Figure 1).
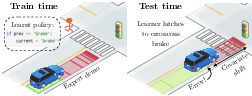
Figure 1: A common example of feedback-driven covariate shift in self-driving. At train time, the robot learns that the previous action (Brake) accurately predicts the current action almost all the time. At test time, when the learner mistakenly chooses to Brake, it continues to choose Brake, creating a bad feedback cycle that causes it to diverge from the expert.
The Three Regimes of Covariate Shift
Easy Regime
In this regime, the expert’s actions are realizable within the policy class, implying that as data volume grows, the BC error approaches zero. Current benchmarks in imitation learning often fall into this category, where even simple BC methods perform well due to sufficient exploration of the environment by the demonstrator, suspecting an idealized assumption of expert state coverage.
Hard Regime
This represents the worst-case scenario where the policy class does not encompass the expert's policy, leading to persistent, compounding errors (O(T2ϵ)). Such errors cannot be mitigated without interactive, expert-guided interventions like those facilitated by DAgger.
Goldilocks Regime
The regime captures a middle ground where the expert is not realizable, but states visited by the learner maintain a bounded density ratio relative to the expert's distribution. Here, techniques like ALICE can utilize simulators to correct covariate shifts leveraging cached demonstrations, without necessitating online expert queries (Figure 2).
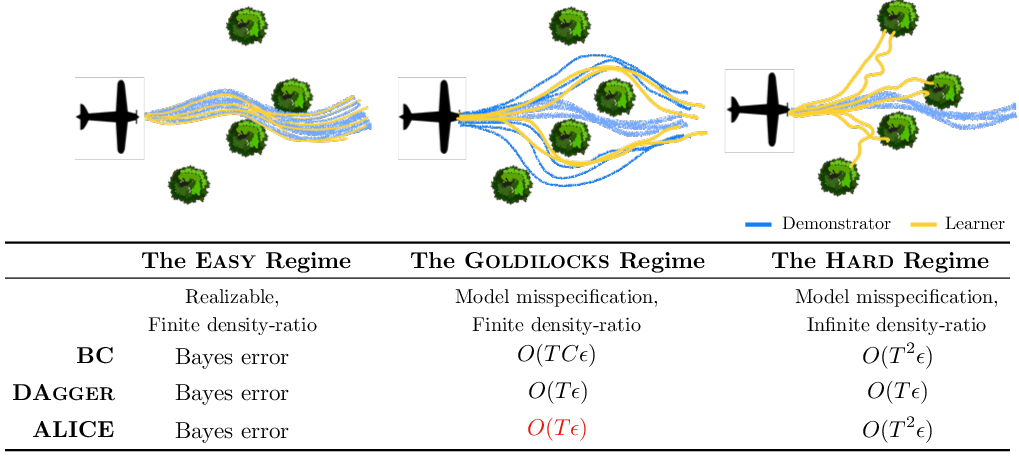
Figure 2: Spectrum of feedback-driven covariate shift regimes. Consider the case of training a UAV to fly through a forest using demonstrations (blue). In Easy regime, the demonstrator is realizable, while in the Goldilocks and Hard regime, the learner (yellow) is confined to a more restrictive policy class. While model mispecification usually requires interactive demonstrations, in the Goldilocks regime, ALICE achieves O(Tϵ) without interactive query.
Addressing the Covariate Shift
The paper introduces ALICE (Aggregate Losses to Imitate Cached Experts), a family of algorithms aiming to adjust the density ratio during policy training to mitigate covariate shift. ALICE employs several strategies for aligning training and real-world distributions, such as reweighting based on estimated density ratios and matching moment distributions of future states between the expert and learner using simulators (Figure 3).
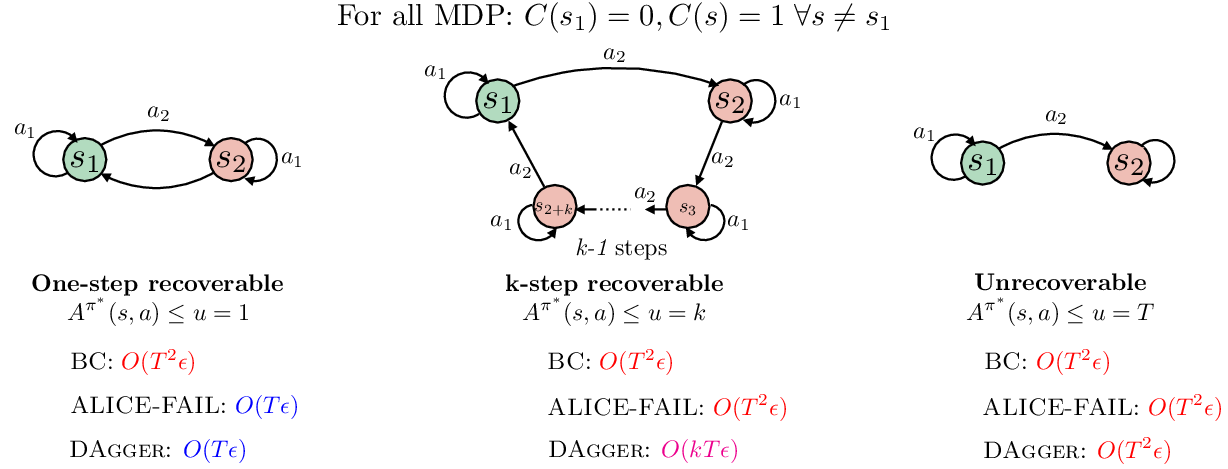
Figure 3: Three different MDPs with varying recoverability regimes. For all MDPs, C(s1)=0 and C(s)=1 for all s=s1. The expert deterministic policy is therefore expert(s1)=a1 and expert(s)=a2 for all s=s1. Even with one-step recoverability, BC can still result in O(T2ϵ) error. For >1-step recoverability, even Fail slides to O(T2ϵ), while DAgger can recover in k steps leading to O(kTϵ). For unrecoverable problem, all algorithms can go up to O(T2ϵ). Hence recoverability dictates the lower bound of how well we can do in the model misspecified regime.
Evaluation and Benchmark Challenges
The authors emphasize the gap between current benchmarks and real-world IL challenges. They call for new benchmarks that replicate the complexity of actual tasks, citing the inadequacies of existing environments. Proposed benchmarks should require comprehensive state coverage, introduce scalable difficulty, and measure success by policy’s on-policy performance without interactive expert involvement.
Conclusion
The paper clarifies critical misinterpretations around causality and covariate shifts, proposing a framework through ALICE to alleviate feedback-driven covariate shift in IL without excessive reliance on interactive experts. A significant challenge remains in designing and establishing robust benchmarks to facilitate this approach's validation and development across IL applications.


