Attention Aware Cost Volume Pyramid Based Multi-view Stereo Network for 3D Reconstruction

Abstract: We present an efficient multi-view stereo (MVS) network for 3D reconstruction from multiview images. While previous learning based reconstruction approaches performed quite well, most of them estimate depth maps at a fixed resolution using plane sweep volumes with a fixed depth hypothesis at each plane, which requires densely sampled planes for desired accuracy and therefore is difficult to achieve high resolution depth maps. In this paper we introduce a coarseto-fine depth inference strategy to achieve high resolution depth. This strategy estimates the depth map at coarsest level, while the depth maps at finer levels are considered as the upsampled depth map from previous level with pixel-wise depth residual. Thus, we narrow the depth searching range with priori information from previous level and construct new cost volumes from the pixel-wise depth residual to perform depth map refinement. Then the final depth map could be achieved iteratively since all the parameters are shared between different levels. At each level, the self-attention layer is introduced to the feature extraction block for capturing the long range dependencies for depth inference task, and the cost volume is generated using similarity measurement instead of the variance based methods used in previous work. Experiments were conducted on both the DTU benchmark dataset and recently released BlendedMVS dataset. The results demonstrated that our model could outperform most state-of-the-arts (SOTA) methods. The codebase of this project is at https://github.com/ArthasMil/AACVP-MVSNet.

• The paper introduces AACVP-MVSNet that integrates self-attention and a coarse-to-fine depth inference strategy to enhance 3D reconstruction.
• It employs a cost volume pyramid with iterative depth residual refinement, demonstrating improved performance over DTU and BlendedMVS benchmarks.
• Experimental results show that the network achieves higher completeness, accuracy, and memory efficiency compared to state-of-the-art methods.

Attention Aware Cost Volume Pyramid Based Multi-view Stereo Network for 3D Reconstruction

This paper introduces an Attention Aware Cost Volume Pyramid Multi-view Stereo Network (AACVP-MVSNet) designed for 3D reconstruction from multi-view images. The network employs a coarse-to-fine depth inference strategy to achieve high-resolution depth maps by iteratively refining depth estimations across multiple levels. Self-attention layers are integrated into the feature extraction block to capture long-range dependencies, and a similarity measurement is used for cost volume generation. The authors validate the model's performance on the DTU benchmark and BlendedMVS datasets, demonstrating improvements over state-of-the-art methods.

Network Architecture and Feature Extraction

The AACVP-MVSNet architecture involves an image pyramid where multi-view images are downsampled to various levels. A weights-shared feature extraction block processes images at each level, starting with the coarsest level ($L$) and refining iteratively. The initial depth map is estimated at the coarsest level, and depth maps at finer levels are upsampled from the previous level with pixel-wise depth residuals. This iterative refinement uses a cost volume pyramid $\{\mathbf{C}^i\}(i = L,L-1,\cdots, 0)$. The network assumes known camera intrinsic matrix, rotation matrix, and translation vector $$\{\mathbf{K}_i,\mathbf{R}_i, \mathbf{t}_i \}_{i=0}^N$$ for all input views.

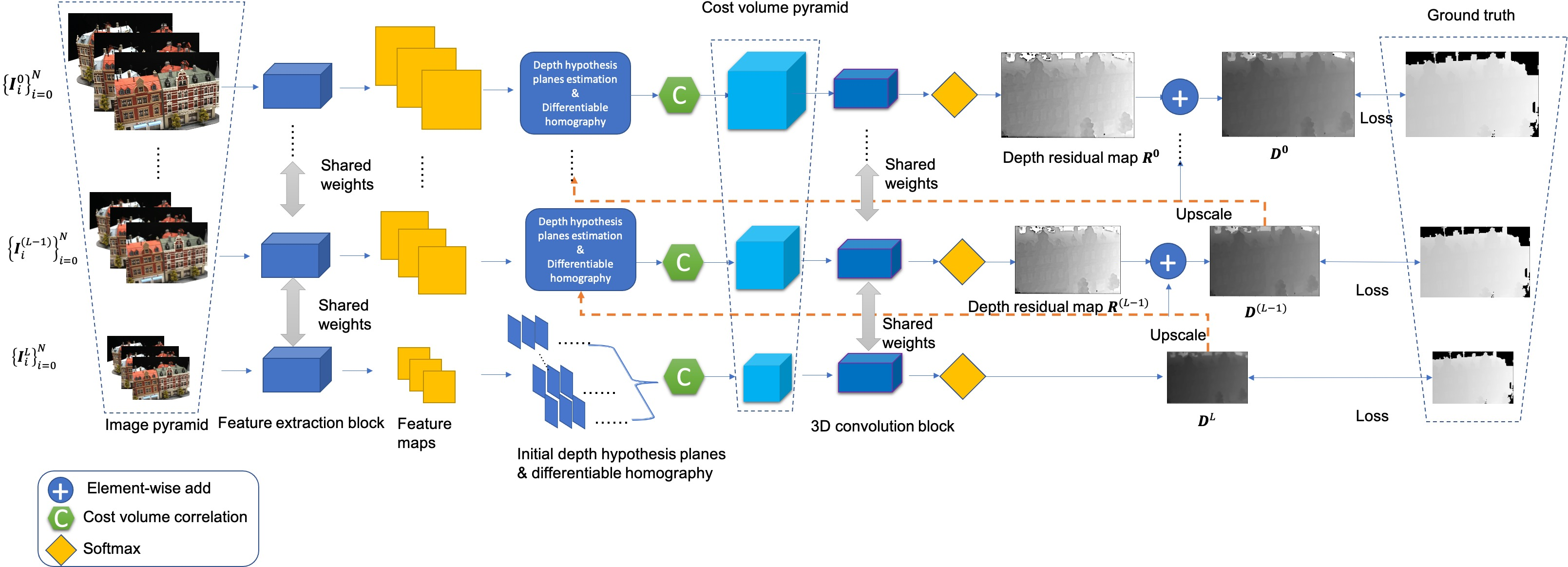
Figure 1: The network structure of AACVP-MVSNet.

The feature extraction block consists of eight convolutional layers and a self-attention layer with 16 output channels, each followed by a Leaky ReLU (Figure 2).

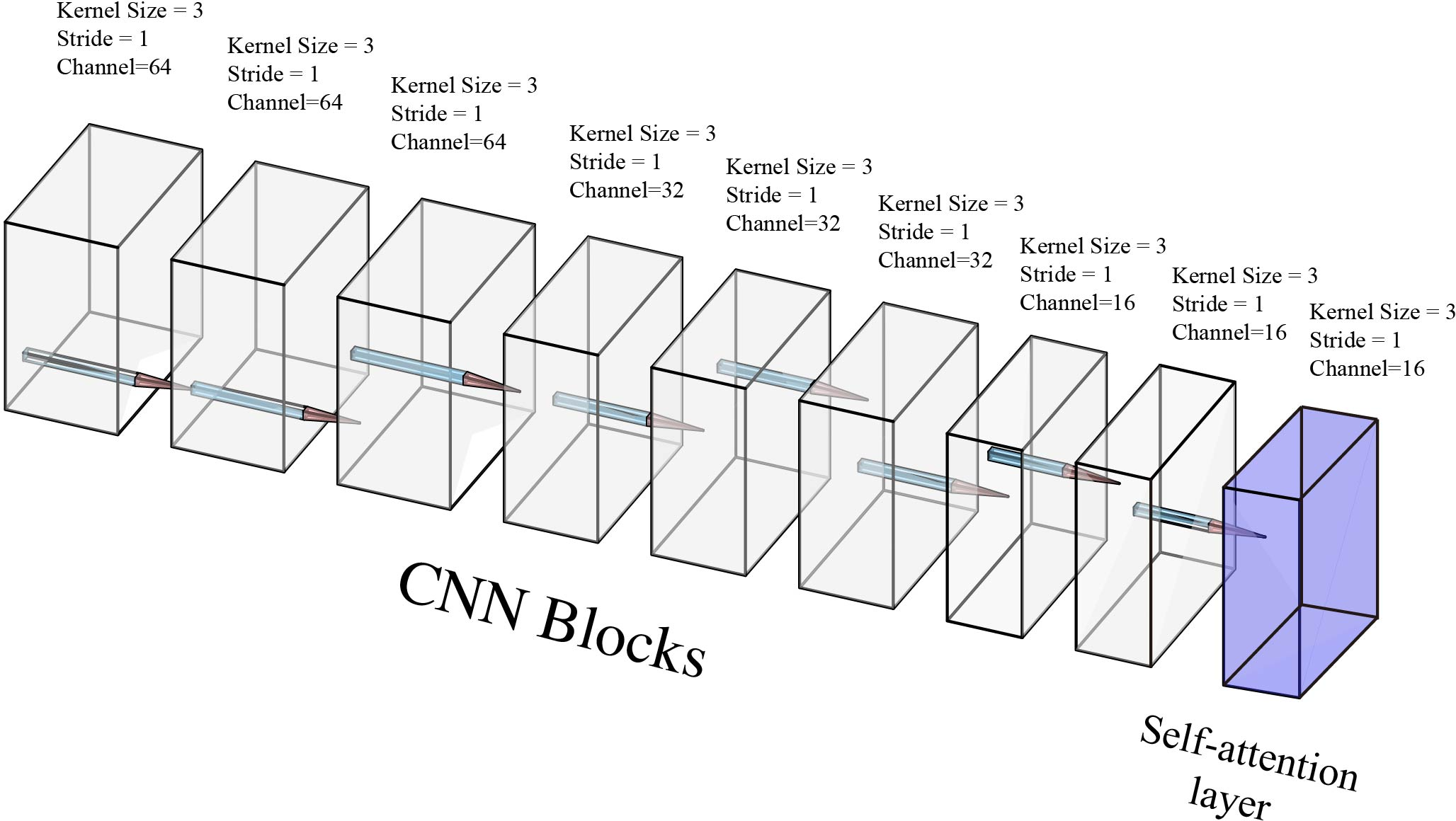
Figure 2: The self-attention based feature extraction block.

The self-attention mechanism focuses on capturing essential information for depth inference by modeling long-distance interactions. The self-attention computation is formulated as:

$$y_{ij} = \sum_{a,b\in \mathbf{B}} \text{Softmax}_{ab}(\mathbf{q}_{ij}^{\rm{T}}\mathbf{k}_{ab}+\mathbf{q}_{ij}^{\rm{T}}\mathbf{r}_{a-i,b-j}) \mathbf{v}_{ab}$$

where $\mathbf{q}_{ij}$, $\mathbf{k}_{ab}$, and $\mathbf{v}_{ab}$ represent queries, keys, and values, respectively, and $\mathbf{r}_{a-i,b-j}$ denotes the relative position embedding (Figure 3).

Figure 3: Convolution layer versus self-attention layer.

The hierarchical feature extraction involves building an image pyramid of $(L+1)$ levels for input images and obtaining hierarchical representations at the $L$-th level. The extracted feature maps at the $l$-th level are denoted by $$\{\mathbf{f}_{i}^L\}\in \mathbb{R}^{H/2^l\times W/2^l\times Ch}$$.

Coarse-to-Fine Depth Estimation

The network constructs a cost volume pyramid (CVP) for depth map inference at the coarsest resolution and depth residual estimation at finer scales. For depth inference at the coarsest resolution, the cost volume is constructed by sampling $M$ fronto-parallel planes uniformly within the depth range $(d_{min},d_{max})$:

$d_m = d_{min} + m (d_{max} - d_{min}) / M$

The differentiable homography matrix $\mathbf{H}^L_i(d)$ transforms feature maps from source views to the reference image. Instead of variance-based feature aggregation, the authors use average group-wise correlation to compute similarity between feature maps. The similarity between the $i$-th group feature maps between the reference image and the $j$-th wrapped image at hypothesized depth plane $d_m$ is:

$$\mathbf{S}^{i,L}_{j,d_m} = \frac{1}{Ch/G} \left<\mathbf{f}^{i,L}_{ref}(d_m),\mathbf{f}^{i,L}_{j}(d_m) \right>$$

The aggregated cost volume $\mathbf{C}^L$ is the average similarity of all views. The probability volume $\mathbf{P}^L$ is generated using a 3D convolution block, and the depth map is estimated as:

$$\mathbf{D}^L(\mathbf{p}) = \sum_{m=0}^{M-1} d_m \mathbf{P}^L({\mathbf{p},d_m})$$

Figure 4: The depth searching range.

For depth residual estimation at finer scales, such as level $(L-1)$, the residual map $\mathbf{R}^{(L-1)}$ is estimated as:

$$\mathbf{R}^{(L-1)} = \sum_{m=-M/2}^{M/2}r_{\mathbf{p}}(m)\mathbf{P}_{\mathbf{p}}^{(L-1)}(r_{\mathbf{p}})$$

$$\mathbf{D}^{(L-1)}(\mathbf{p}) = \mathbf{R}^{(L-1)} + \mathbf{D}_{upscale}^{(L)}(\mathbf{p})$$

where $r_{\mathbf{p} = m \Delta d_{\mathbf{p}}$ represents the depth residual, and $\Delta d_{\mathbf{p} = l_{\mathbf{p}/M$ is the depth interval. The depth searching range and depth interval are key parameters for depth residual estimation.

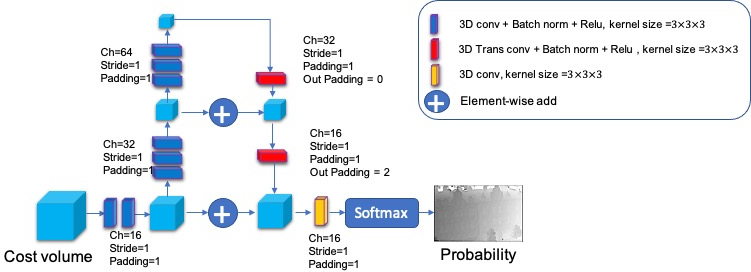
Figure 5: The structure of 3D convolution block.

The cost volume is built using the same method as in the coarsest level. The depth map $\mathbf{D}^{(L-1)}$ is achieved after a 3D convolution block and softmax operation for $\mathbf{P}^{(L-1)}$. The iterative depth map estimation process continues until the finest level is reached, resulting in the final depth map $\mathbf{D}^0$.

Experimental Results

Experiments were conducted on the DTU dataset and the BlendedMVS dataset. The DTU dataset was used for quantitative analysis, while the BlendedMVS dataset was used for qualitative analysis due to the absence of official ground truth. The training on the DTU dataset was performed with images of size $160 \times 128$ pixels, and the trained weights were evaluated on full-sized images. The training on the BlendedMVS dataset used low-resolution images ($768\times 576$ pixels).

Figure 6: 3D reconstruction result of 9th scene in DTU dataset.

The results on the DTU dataset demonstrate that AACVP-MVSNet outperforms other methods in terms of completeness and overall accuracy, as shown in the provided table. The method also exhibits lower memory usage compared to baseline networks that use variance-based cost volume generation (Figure 7, Figure 8).

Figure 7: 3D reconstruction result of 15th scene in DTU dataset.

Figure 8: 3D reconstruction result of 49th scene in DTU dataset.

On the BlendedMVS dataset, qualitative results show that the generated point clouds are smooth and complete. Comparison of depth map generation results between AACVP-MVSNet and MVSNet reveals that AACVP-MVSNet produces higher-resolution depth maps with more high-frequency details.

Figure 9: Results on the BlendedMVS dataset.

Figure 10: Comparison of depth inference results between MVSNet and AACVP-MVSNet.

Ablation studies were performed to evaluate the impact of multi-head self-attention layers and the number of views used in training and evaluation. The results indicate that increasing the number of views for evaluation generally improves reconstruction quality.

Figure 11: Training loss with $nViews_{T} = 3,5,7$.

Conclusion

The AACVP-MVSNet architecture combines self-attention mechanisms and similarity measurement-based cost volume generation for 3D reconstruction. Trained iteratively with a coarse-to-fine strategy, it achieves performance superior to state-of-the-art methods on benchmark datasets. Future work may focus on improving the depth searching range determination and adaptive parameter selection for hypothesized depth planes. Additionally, research into unsupervised MVS methods could extend the application of MVS networks to more diverse scenarios.