An additive algorithm for origami design

Abstract: Inspired by the allure of additive fabrication, we pose the problem of origami design from a new perspective: how can we grow a folded surface in three dimensions from a seed so that it is guaranteed to be isometric to the plane? We solve this problem in two steps: by first identifying the geometric conditions for the compatible completion of two separate folds into a single developable four-fold vertex, and then showing how this foundation allows us to grow a geometrically compatible front at the boundary of a given folded seed. This yields a complete marching, or additive, algorithm for the inverse design of the complete space of developable quad origami patterns that can be folded from flat sheets. We illustrate the flexibility of our approach by growing ordered, disordered, straight and curved folded origami and fitting surfaces of given curvature with folded approximants. Overall, our simple shift in perspective from a global search to a local rule has the potential to transform origami-based meta-structure design.

• The paper introduces an additive algorithm for growing quad origami surfaces from a seed, ensuring developability and preserving key folding constraints.
• It employs geometric compatibility at vertices through flap angle parameterization to integrate folds seamlessly and maintain design flexibility.
• The algorithm enables rapid prototyping of various origami designs, including Miura-ori tessellations and Brownian ribbons, with significant engineering applications.

An Additive Algorithm for Origami Design

The paper presents a novel framework for the design of developable quad origami surfaces using an additive algorithm that extends folded structures without compromising developability. The motivation is drawn from additive fabrication techniques, focusing on growing a folded surface from a seed such that the new surface remains isometric to the plane.

Geometric Foundations and Single Vertex Construction

At the core of the approach is establishing geometric compatibility for the completion of four-fold vertices. The paper identifies crucial angle constraints required to integrate two separate folds into a single developable vertex. Specifically, the vertex construction depends on the choice of a flap angle, $\alpha_i$, which parameterizes the set of possible growth directions at a vertex, leading to the development of compatible quad origami strips.

Figure 1: Construction of Quad Origami and the geometric constraints for vertex integration.

Additive Algorithm

The additive algorithm is outlined as a series of steps to grow new strips from a seed with predefined flap angles and edge constraints. This process ensures compatibility with the existing folded model and maintains the properties of rigid-foldability and flat-foldability. The algorithm effectively circumvents the traditional complexities associated with global optimization or specific geometric constructions, offering a scalable approach.

Figure 2: Additive Algorithm flow and determination of DOFs for strip creation.

Vertex and Strip Design Dynamics

The dynamics of vertex growth are scrutinized through the parameterization of flap angles which dictate design flexibility. Characteristics such as flat-foldability and trivial continuation are addressed, with implications on designing complex folded surfaces. The singular configurations and operational space of growth directions are pivotal in expanding the design possibilities of origami structures.

Figure 3: Dynamics of Vertex and Strip design showcasing parameter space and compatibility.

Applications in Origami Design

The method's flexibility is demonstrated through the inverse design of varied quad origami structures, ranging from straight and curved to ordered and disordered configurations. By employing the additive algorithm, complex surface approximations such as generalized Miura-ori tessellations and Brownian ribbons are achieved. Each design example underscores the potential for direct translation of mathematical theory into real-world applications.

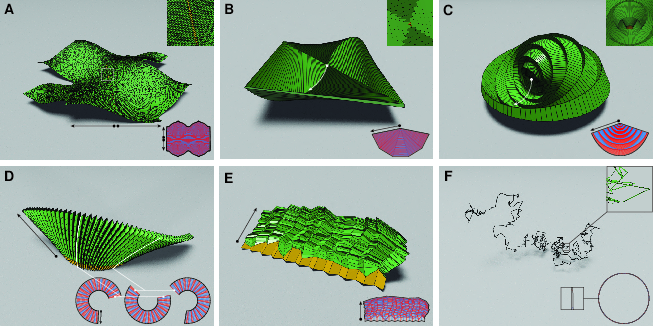
Figure 4: Several advanced origami designs created using the additive algorithm, showcasing different typologies.

Conclusion

The proposed additive algorithm facilitates a comprehensive exploration of quad origami design space without the limitations posed by previous piecemeal solutions. By emphasizing boundary flexibility, it paves the way for rapid prototyping of origami-based structures. Future directions could include integrating non-Euclidean geometries and extending freeform design capabilities. The intersection of geometric flexibility and computational design heralds significant advancements in the fields of engineering, architecture, and material science.