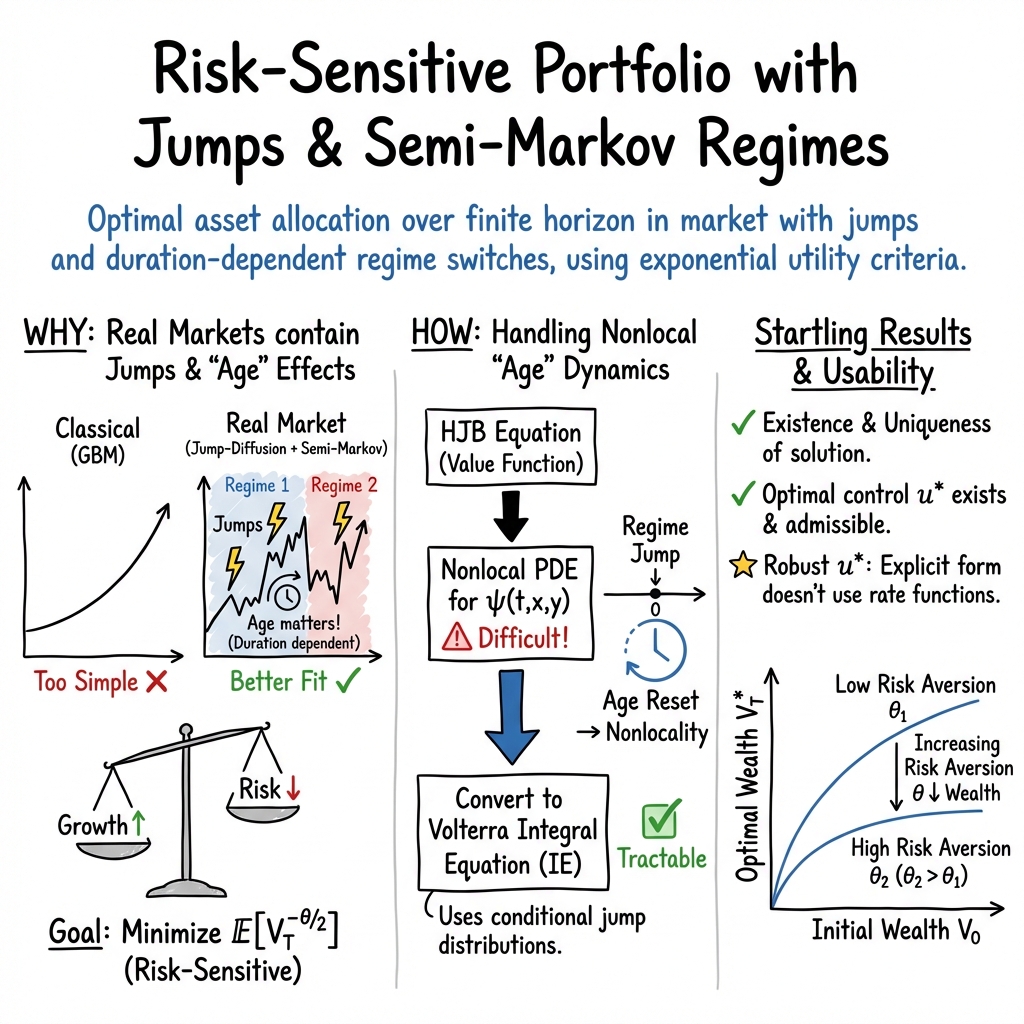
Risk Sensitive Portfolio Optimization in a Jump Diffusion Model with Regimes
Abstract: This article studies a portfolio optimization problem, where the market consisting of several stocks is modeled by a multi-dimensional jump-diffusion process with age-dependent semi-Markov modulated coefficients. We study risk sensitive portfolio optimization on the finite time horizon. We study the problem by using a probabilistic approach to establish the existence and uniqueness of the classical solution to the corresponding Hamilton-Jacobi-Bellman (HJB) equation. We also implement a numerical scheme to investigate the behavior of solutions for different values of the initial portfolio wealth, the maturity, and the risk of aversion parameter.
Summary
- The paper formulates and solves a risk-sensitive portfolio optimization problem using jump diffusion processes with semi-Markov regime switches.
- It employs a Hamilton-Jacobi-Bellman equation transformed into a system of linear PDEs and Volterra integral formulations for numerical approximation.
- Numerical results showcase optimal wealth variations in response to initial investments, maturity, and risk aversion, highlighting regime effects.
Risk Sensitive Portfolio Optimization in a Jump Diffusion Model with Regimes
Introduction
The paper "Risk Sensitive Portfolio Optimization in a Jump Diffusion Model with Regimes" (1603.09149) examines a portfolio optimization problem within financial markets modeled by multidimensional jump diffusion processes with age-dependent semi-Markov modulated coefficients. The study is conducted within a finite time horizon, employing a probabilistic approach to establish the existence of a classical solution to the associated Hamilton-Jacobi-Bellman (HJB) equation.
A comprehensive numerical scheme is implemented to explore the behaviors of solutions under varying initial portfolio wealth, maturity, and risk aversion parameters. The authors extend the scope of portfolio optimization techniques beyond typical Gaussian assumptions by incorporating discontinuous asset dynamics captured through jump diffusion models. Semi-Markov processes are employed for regime switching, allowing for age-dependent transitions—providing a tractable framework to handle real-world phenomena like volatility clustering and investor behavior changes based on market conditions.
Figure 1: Finite horizon risk sensitive optimal wealth function
Theoretical Framework
Market Model
The financial market dynamics are represented as a regime-switching model where a pure jump process governs the asset regimes. Asset prices follow stochastic differential equations (SDEs) driven by combinations of drift, volatility, and jump components. The jump diffusion model enables the capture of price discontinuities, enhancing empirical fidelity compared to models restricted to deterministic time evolution of parameters.
Risk Sensitive Criteria
The risk-sensitive portfolio optimization problem is framed using exponential utility functions, capturing the tradeoff between expected growth rates and variance. This method extends Merton's utility maximization approach by considering parameterized exponential utility functions in portfolio optimization, allowing investors to choose appropriate parameters based on their risk tolerance.
HJB Equation and Numerical Approximations
The paper formulates the risk-sensitive optimization as an HJB equation decomposed into a system of linear first-order partial differential equations (PDEs). Techniques for solving these PDEs include transforming the HJB equation to a Volterra integral equation and demonstrating the existence and uniqueness of the solution. Numerical experiments validate the theoretical findings, offering insights into optimal portfolio allocation patterns across varying market conditions.
Figure 2: Optimal wealth function vs risk aversion parameter
Numerical Results
Numerical simulations reveal how optimal wealth varies with initial investment levels, maturity periods, and risk aversion parameters. Wealth trajectories exhibit concave behavior against initial investment levels, resonating with financial theories of diminishing marginal returns. Conversely, the optimal wealth displays linear growth concerning investment maturity, affirming expected financial planning principles.
Notably, the investigation highlights a consistent hierarchy in optimal wealth corresponding to different market regimes, driven by varying drift and volatility terms. Figures illustrate the role of risk aversion encapsulated in exponential utility adjustments—the higher the aversion, the lower the resultant optimal wealth, underscoring the pragmatic balance between risk and return in portfolio decisions.
Conclusion
The research provided a detailed exploration of risk-sensitive portfolio optimization within a regime-switching jump diffusion market model. By linking rigorous mathematical derivations with practical numerical simulations, the study extends classical portfolio management paradigms to incorporate discontinuous asset behavior and nuanced market switching mechanisms. This advancement is pertinent for adapting contemporary financial strategies amidst volatile market conditions and economically active regimes.
Whiteboard
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Practical Applications
Overview
This paper delivers a practically deployable framework for dynamic, risk-sensitive portfolio allocation in markets with discontinuities (jumps) and regime shifts whose transition intensities depend on how long a regime has lasted (age-dependent semi-Markov switching). Its contributions include:
- A market model that captures duration dependence in regimes (a documented empirical feature), with independent regime processes per asset.
- A risk-sensitive control formulation over a finite horizon and a constructive method to obtain the optimal feedback control.
- A tractable reduction of a nonlocal HJB PDE to a Volterra integral equation of the second kind, with existence/uniqueness and a robust numerical quadrature scheme.
- An explicit, continuous optimal policy map u*(t, x) that depends only on time and regimes (not on wealth), aiding implementation.
Below are actionable applications, grouped by time-to-deploy. Each item includes sector links, potential tools/products/workflows, and key assumptions/dependencies.
Immediate Applications
- Finance and Asset Management: Risk-sensitive dynamic allocation under regime duration and jumps
- Use case: Quantitative funds and asset managers can deploy the risk-sensitive allocation rule u*(t, x) to balance expected growth and variance while accounting for jump risks and regime persistence.
- Sectors: Finance (asset management, hedge funds), Insurance (investment units), Treasury.
- Tools/products/workflows:
- Build a calibration pipeline:
- 1) Identify regimes per asset via Hidden semi-Markov models (HSMM) or supervised filters.
- 2) Estimate age-dependent hazard rates λl_{ij}(y) with survival analysis (parametric or nonparametric).
- 3) Calibrate jump measures νj and jump-size functions η{lj} from returns (e.g., EM or GMM with finite-activity jumps).
- 4) Estimate drift/volatility by regime.
- Implement the paper’s Volterra-based HJB solver (quadrature) to compute ψ and h_θ, then u*(t, x).
- Embed u*(t, x) into a portfolio engine for periodic rebalancing (e.g., daily/weekly) with constraints from A1–A3 and admissibility.
- Assumptions/dependencies: Frictionless trading; finite-activity jumps; invertible covariance (A3); independence across asset regimes; feasibility of regime and hazard estimation; selection of risk-sensitivity θ; enforcement of admissible controls ensuring wealth positivity, i.e., [u*η(z)]_j ≥ −1+δ.
- Risk Management: Regime-age–aware stress testing and early warning
- Use case: Banks/insurers can use P_{t,x,y}(ℓ(t)=l) and F_{τl|l}(·|x,y) to assess the likelihood and timing of the next regime shift, improving scenario design for VaR/ES and tail risk.
- Sectors: Finance (ERM, market risk), Insurance (ALM risk), Clearinghouses.
- Tools/products/workflows:
- Add a “regime-age dashboard” showing the conditional distribution of next transition time and the component most likely to switch next.
- Use the model to stress the timing and magnitude of jumps/regime shifts and quantify capital buffer impacts under the risk-sensitive criterion.
- Assumptions/dependencies: Reliable hazard estimation; mapping business lines to regime states; backtesting with historical regimes to validate predictive usefulness.
- Trading and Execution: Position sizing and de-risking rules under prolonged calm or stress
- Use case: Systematic strategies can scale positions down when regime age indicates elevated transition hazard, mitigating jump and regime-switch drawdowns.
- Sectors: Systematic trading, Market making (inventory risk), Treasury.
- Tools/products/workflows:
- Hook a lightweight “regime-age signal” (derived from F_{τl|l}) into position-sizing logic.
- Combine with the risk-sensitive optimizer to modulate leverage based on regime persistence.
- Assumptions/dependencies: Intraday to daily updates of regime age; low-latency estimation not required if rebalanced at low frequency.
- Analytics/Software: Libraries for nonlocal HJBs via Volterra reduction
- Use case: Quant teams and analytics vendors can implement a reusable module to solve nonlocal HJBs encountered in hybrid jump–diffusion controls.
- Sectors: Fintech, Quant research groups.
- Tools/products/workflows:
- Package a C++/Python library:
- Solvers for the Volterra integral equation (quadrature) with convergence checks.
- APIs for hazard-rate inputs, jump measures, and regime grids.
- Integrate with backtesting frameworks (e.g., Zipline, qlib) and risk engines.
- Assumptions/dependencies: Numerical stability and discretization choices; memory scaling with regime grid size kn+1.
- Academia and Education: Teaching and benchmarking advanced stochastic control
- Use case: Graduate courses and research seminars can adopt the paper’s age-dependent regime model and the PDE→Volterra methodology as a modern tractable template.
- Sectors: Academia, Quant training programs.
- Tools/products/workflows:
- Release reproducible notebooks for calibration, solving ψ via quadrature, and simulating optimal wealth trajectories.
- Compare GBM/Markov-switching baselines vs semi-Markov (“age-dependent”) to highlight duration effects.
- Assumptions/dependencies: Availability of example datasets; code for HSMM calibration.
- Commodities, Energy, and Crypto: Regime-aware allocation in jumpy, regime-prone markets
- Use case: Apply the same risk-sensitive control to markets with known jump risk and persistent regimes (e.g., contango/backwardation shifts, crypto volatility cycles).
- Sectors: Energy trading, Commodity funds, Crypto quant funds.
- Tools/products/workflows: As in finance application, with domain-specific regime definitions (e.g., inventory/seasonality for commodities).
- Assumptions/dependencies: Market-specific regime labeling; calibrated jump distributions for each asset class.
- Robo-Advisory/Daily Life (simplified rule-of-thumb version)
- Use case: Incorporate a “prolonged-calm de-risking” overlay in multi-asset ETFs or robo-advisors to temper risk after extended low-volatility periods.
- Sectors: WealthTech, Retail investing.
- Tools/products/workflows:
- Use a coarse two-regime proxy (calm/turbulent) with an age threshold to scale equities exposure modestly.
- Periodic recalibration to avoid overfitting.
- Assumptions/dependencies: Simplification from full semi-Markov apparatus; guardrails to prevent excessive turnover and whipsawing; investor suitability and disclosures.
Long-Term Applications
- Regulatory Stress Testing and Macroprudential Policy
- Use case: Supervisors can incorporate duration-dependent regime risks (e.g., prolonged low-vol environments preceding sharp transitions) into systemic stress scenarios and guidance.
- Sectors: Central banks, Prudential regulators.
- Tools/products/workflows:
- Scenario generators using age-dependent hazards for joint regime transitions across sectors.
- Templates for banks to report risk-sensitive capital impacts under duration-aware stress.
- Assumptions/dependencies: Industry-standard calibration protocols; data-sharing to estimate cross-institution regime hazards.
- Correlated Regime Processes and Systemic Risk
- Use case: Extend from independent asset regimes to correlated or coupled age-dependent regimes to capture contagion/systemic behavior.
- Sectors: Finance, Macro risk, Network risk.
- Tools/products/workflows:
- Develop multi-dimensional semi-Markov models with dependence (copulas, common shocks).
- Generalize the HJB→Volterra reduction and numerics to coupled regimes.
- Assumptions/dependencies: New theory for dependence structures; higher computational cost; careful identifiability in calibration.
- Transaction Costs, Illiquidity, and Constraints
- Use case: Bring the risk-sensitive control into realistic trading with costs, finite liquidity, no-shorting/position limits, and market-impact.
- Sectors: Asset management, Execution research.
- Tools/products/workflows:
- Add frictions into the control problem; derive approximate policies or policy iteration schemes.
- Backtest turnover/risk trade-offs; integrate execution algorithms.
- Assumptions/dependencies: Additional model layers (impact, slippage); potentially no closed form u*(t, x); need for scalable approximate dynamic programming.
- Insurance and Pensions: ALM under Semi-Markov Regimes with Jumps
- Use case: Long-horizon liability-driven investing using risk-sensitive criteria to limit drawdowns around regime transitions.
- Sectors: Insurance (life, annuities), Pension funds.
- Tools/products/workflows:
- Joint asset-liability simulation under semi-Markov regimes.
- Optimize strategic tilts with risk budgets and solvency constraints.
- Assumptions/dependencies: Integration with stochastic liability models; regulatory acceptance.
- Derivatives Pricing, Hedging, and New Structured Products
- Use case: Price and hedge options under age-dependent regime/jump dynamics; design products tied to regime age (e.g., coupons contingent on persistence).
- Sectors: Derivatives desks, Structured products.
- Tools/products/workflows:
- Extend valuation PDEs with semi-Markov coefficients; risk-sensitive hedging overlays.
- Monte Carlo with hazard-driven path branching.
- Assumptions/dependencies: Calibration of λl_{ij}(y) from option-implied surfaces; risk-neutral measure consistency.
- ML-Enhanced Calibration and Filtering
- Use case: Use deep survival models or Bayesian nonparametrics to estimate age-dependent hazards and regime states online.
- Sectors: Fintech, Quant research.
- Tools/products/workflows:
- Neural HSMMs for real-time filtering of regimes and their ages.
- Uncertainty quantification feeding into robust control (distributionally robust risk-sensitive variants).
- Assumptions/dependencies: Data intensity; model validation to prevent overfitting; governance for ML in risk.
- Real-Time SaaS Risk Platform
- Use case: Commercialize a platform that ingests market data, infers regime ages, computes u*(t, x), and serves APIs for portfolio/risk systems.
- Sectors: Fintech, Risk analytics vendors.
- Tools/products/workflows:
- Cloud microservices: calibration, HJB–Volterra solver, orchestration, monitoring.
- UI for regime-age maps, hazard curves, policy recommendations.
- Assumptions/dependencies: Client-specific constraints; SLAs; explainability and compliance.
- Cross-Domain Transfer: Reliability Engineering and Maintenance Scheduling
- Use case: Apply the age-dependent switching + risk-sensitive control methodology to systems whose failure/repair modes depend on time-in-state (e.g., industrial equipment).
- Sectors: Energy, Manufacturing, Robotics (safety/maintenance).
- Tools/products/workflows:
- Control policies to minimize risk of catastrophic jumps (failures) subject to cost; solve analogous nonlocal HJBs via Volterra reduction.
- Assumptions/dependencies: Domain-specific jump/transition models; mapping financial “wealth” to system performance/utility.
Key Global Assumptions/Dependencies Impacting Feasibility
- Market and data:
- Frictionless market, continuous trading, and finite-activity jumps assumed; transaction costs and liquidity need explicit modeling for production.
- Reliable regime identification and hazard estimation are prerequisites; often requires HSMMs and sufficient history.
- Independence of regime processes across assets (as assumed here) simplifies modeling but may be unrealistic in crises; correlated extensions raise complexity.
- Mathematical/numerical:
- Invertible diffusion (A3) and admissible controls to ensure positivity needed; risk-sensitive parameter θ must be set by governance/policy.
- Numerical quadrature scales with the size of the regime grid; high dimensions can trigger the curse of dimensionality—parallelization and dimensionality reduction may be necessary.
- Governance/compliance:
- Model risk management, backtesting, and explainability (especially for retail/robo use and regulatory contexts).
- Validation of duration dependence (semi-Markov vs Markov) on the target asset universe before adoption.
Collections
Sign up for free to add this paper to one or more collections.