A network model for cellular aging (1305.5784v3)

Abstract: What is aging? Mechanistic answers to this question remain elusive despite decades of research. Here, we propose a mathematical model of cellular aging based on a model gene interaction network. Our network model is made of only non-aging components - the biological functions of gene interactions decrease with a constant mortality rate. Death of a cell occurs in the model when an essential gene loses all of its interactions to other genes, equivalent to the deletion of an essential gene. Gene interactions are stochastic based on a binomial distribution. We show that the defining characteristic of biological aging, the exponential increase of mortality rate over time, can arise from this gene network model during the early stage of aging. Hence, we demonstrate that cellular aging is an emergent property of this model network. Our model predicts that the rate of aging, defined by the Gompertz coefficient, is approximately proportional to the average number of active interactions per gene and that the stochastic heterogeneity of gene interactions is an important factor in the dynamics of the aging process. This theoretic framework offers a mechanistic foundation for the pleiotropic nature of aging and can provide insights on cellular aging.

• The paper introduces a network-based model explaining cellular aging by integrating reliability theory with stochastic gene interactions.
• It demonstrates that independent modules of essential and non-essential genes can reproduce the exponential mortality patterns observed in Gompertzian aging.
• The analysis reveals how variations in gene interactions account for the Strehler-Mildvan correlation, offering insights into aging mechanisms and potential interventions.

A Network Model for Cellular Aging

This paper introduces a mathematical framework for understanding cellular aging through a model that characterizes aging as an emergent property of gene interaction networks. The model integrates insights from reliability theory and stochastic processes, shedding light on the exponential increase in mortality rates observed with biological aging. The research focuses on incorporating non-aging components within gene networks to elucidate the pleiotropic and stochastic nature of aging observed in biological systems such as yeast.

Model Structure and Foundation

The proposed model begins with the construction of essential network modules, each consisting of one essential gene and multiple non-essential genes. The interactions between genes are characterized by a constant decay rate, denoted by $\lambda$, where the loss of an essential gene results in network failure akin to cellular death (Figure 1).

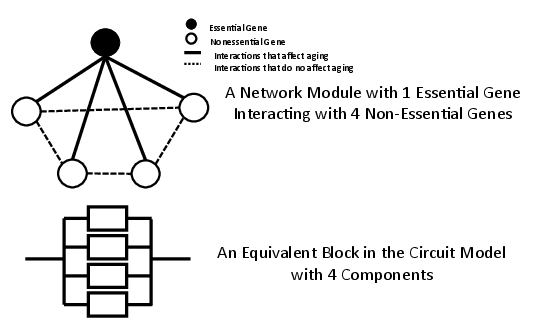
Figure 1: A single essential network module and its equivalent block in the classical circuit model.

The model expands to a network composed of multiple independent modules. Each module functions independently, analogous to serially connected blocks in a classical circuit model, where interaction patterns among non-essential genes do not impact aging dynamics (Figure 2).

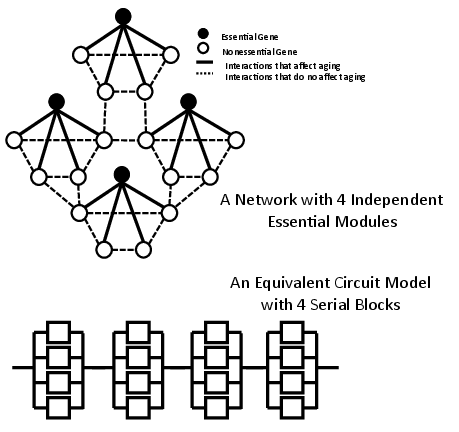
Figure 2: A network with independent modules and its equivalent circuit model.

Emergence of Gompertzian Aging

To simulate the stochastic nature inherent in biological systems, the model introduces randomness in gene interactions. The active status of each interaction follows a binomial distribution with an initial active probability $p$ (Figure 3). This stochastic assumption enables the model to reproduce the exponential increase in mortality rates observed in Gompertzian aging, particularly during the early stages.

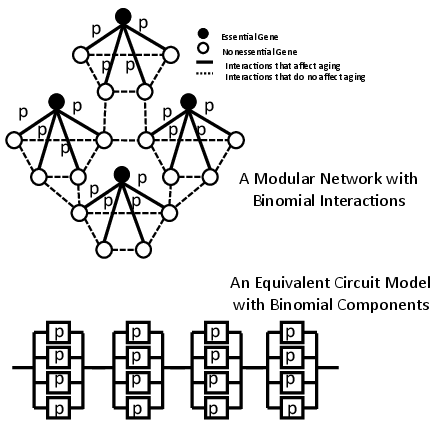
Figure 3: A network model with stochastic interactions and its equivalent circuit model.

The mortality rate of the network is derived from the integration of the stochastic elements, resulting in equations that closely mirror those from Gompertz's law of mortality. The formulation posits that the stochastic variability in gene interactions is key to the aging phenomenon, aligning with observations of diversity in aging rates across yeast populations.

Strehler-Mildvan Correlation

The model successfully accounts for the Strehler-Mildvan correlation—a negative relationship between initial mortality rates and the rate of aging—through variations in network configurations. Changes in the number of gene interactions ($n$) and the probability of their activity ($p$) can explain empirical observations in yeast natural isolates (Figure 4).

Figure 4: Changes of network configurations can lead to the observed Strehler-Mildvan correlation in yeast natural isolates.

Implications and Future Directions

The research emphasizes the importance of stochasticity and network robustness in the emergence of aging, proposing that these properties create variability in biological systems that leads to the Gompertzian mortality curve. The model's predictions align with experimental data on yeast, suggesting that the observed aging characteristics could be driven by intrinsic network features rather than aging-specific genetic programs.

The framework sets the stage for future exploration into cellular renewal mechanisms, non-trivial gene interactions, and the extension of the model to multicellular organisms. The findings encourage a shift in focus toward quantitative, network-centric approaches to studying aging in biological systems, with potential applications in understanding aging-related diseases and intervention strategies.

Conclusion

This paper's contribution to the aging research landscape lies in its robust modeling of cellular aging as an emergent property of complex gene networks. By blending principles from both reliability theory and stochastic processes, the model provides a comprehensive explanation for the variability and universal characteristics of aging observed across different biological taxa. This approach holds promise for advancing our understanding of aging from a systems biology perspective.