’t Hooft Model in 2D QCD

• ’t Hooft Model is an exactly solvable limit of two-dimensional QCD defined by an integral equation that determines discrete meson spectra and exhibits Regge-like scaling.
• The model offers a holographic reformulation by mapping parton variables to the AdS₃ radial coordinate, enabling explicit tests of the AdS₃/CFT₂ correspondence.
• Integrable structures, exemplified by the TQ-Baxter equation, facilitate precise spectral analyses and underpin advancements in lattice simulations and effective field theories.

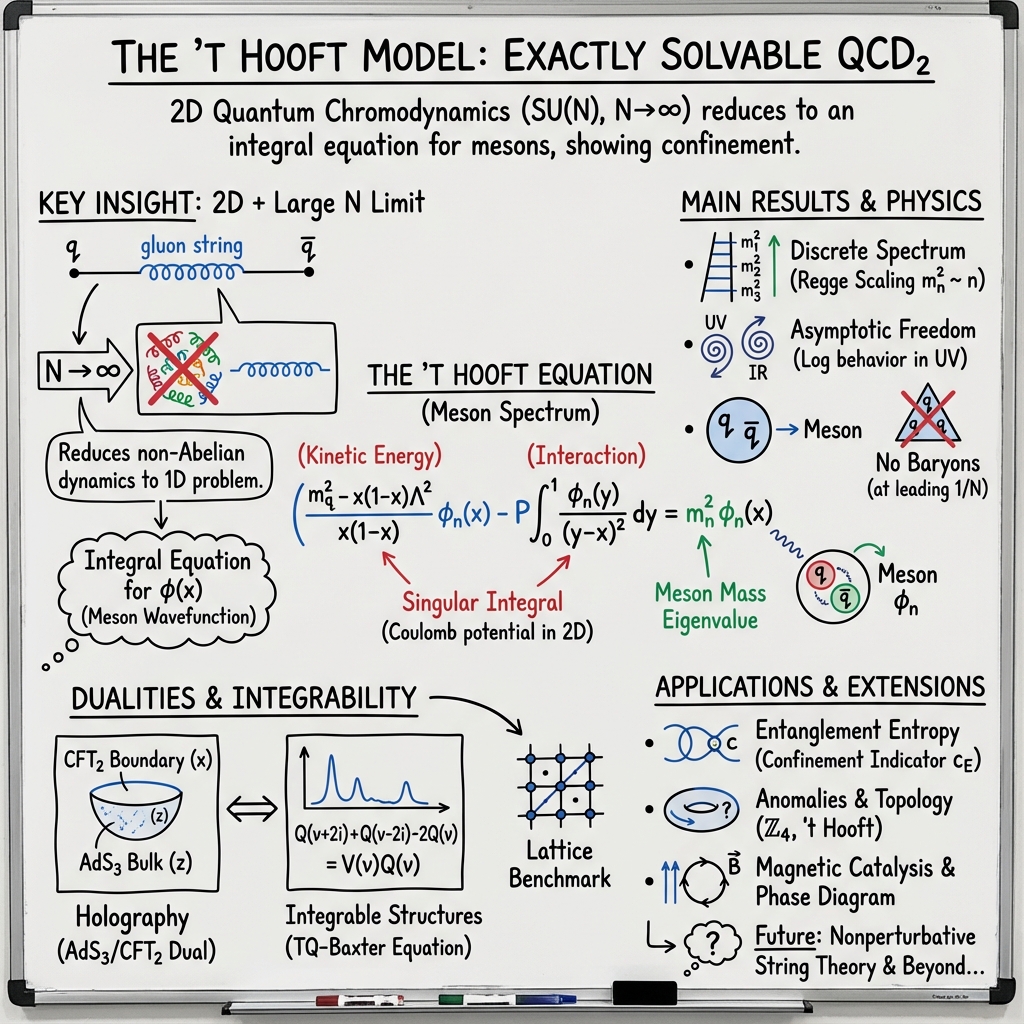
The ’t Hooft Model is the exactly solvable limit of two-dimensional quantum chromodynamics (QCD$_2$) with gauge group $SU(N_c)$ and quarks in the fundamental representation, considered at large $N_c$. Its founding insight was ’t Hooft’s reduction of the non-Abelian gauge dynamics in 1+1D to a self-consistent integral equation for the meson spectrum, revealing a rich structure of confinement, spectral scaling, and strong–weak dualities. Over the past decades, the ’t Hooft model has served as a paradigmatic setting for advances in gauge theory, integrability, entanglement, anomalies, lattice approaches, and holographic dualities.

1. Exact Solution and the ’t Hooft Integral Equation

The core of the ’t Hooft model is the reduction of the non-Abelian dynamics (in the $N_c \to \infty$ limit and with gauge coupling $g$) to the problem of $q\bar q$ bound states governed by the ’t Hooft equation: $$\left(\frac{m_q^2}{\Lambda^2}-1\right)\frac{1}{x(1-x)} \,\varphi_n(x) -\mathcal{P}\!\int_0^1 \frac{\varphi_n(y)}{(y-x)^2}dy =\frac{m_n^2}{\Lambda^2}\,\varphi_n(x)$$ where $x$ $(0<x<1)$ is the longitudinal momentum fraction carried by the quark, $m_q$ is its mass, $\Lambda$ is a scale set by the coupling, $m_n$ labels the meson mass eigenstates, and $\mathcal{P}$ denotes the principal value.

Key properties:

• The spectrum $\{m_n^2\}$ is discrete, with $m_n^2 \sim n$ for large $n$ (Regge-like scaling).
• In the conformal (chiral) limit ($m_q, \Lambda \rightarrow 0$ appropriately), correlation functions exhibit logarithmic behavior expected from 2D asymptotic freedom.
• The eigenfunctions $\varphi_n(x)$ define the partonic content (“parton distribution”) of the mesons.

The model supports only color-singlet mesons as physical states; baryons are absent at leading order in $1/N_c$. The full dynamical content is determined by the above integral equation.

2. Holographic Reformulation and AdS$_3$ Dual

In the conformal ultraviolet limit, the ’t Hooft equation admits a holographic reinterpretation as the equation of motion for a scalar field in AdS$_3$ (0710.3402). Specifically, one can explicitly map the parton variable $x$ to the radial coordinate $z$ of AdS$_3$ using the kernel transform

$$\widetilde{\phi}(z) = \int_0^\infty dx\, K\left(\frac{z^2}{x}\right)\phi(m^2x)$$

where the kernel $K$ employs trigonometric/Bessel function identities such that the bulk solution is $\widetilde{\phi}(z) \propto z J_0(mz)$. This matches the normalizable solution to the Klein–Gordon equation in AdS$_3$ with $m^2=-1$ (the correct dual for a dimension-1 scalar operator). Thus, the model provides a concrete, explicitly solvable realization of the AdS$_3$/CFT$_2$ correspondence “from the boundary,” and allows the holographic checking of two-point functions, scaling, and operator identification. When conformal symmetry is broken (by $\Lambda$), the dual bulk theory is deformed by $z$-dependent potentials and higher-derivative terms reflecting the breaking patterns and “apparent” chiral symmetry breaking in the gauge theory.

3. Integrable Structures: TQ-Baxter Equation and Spectral Analysis

A notable advance is the recognition that the ’t Hooft integral equation is equivalent to a TQ-Baxter equation (Ambrosino et al., 2023). After map to rapidity space ($\theta = \frac{1}{2}\log\frac{x}{1-x}$) and Fourier (or Mellin) transformation, the spectral problem reads

$$\lambda \int_{-\infty}^{+\infty}\!\frac{\pi(\nu-\nu')}{2\sinh[\frac{\pi}{2}(\nu-\nu')]} \Psi(\nu') d\nu' = \bigg[\nu\coth(\frac{\pi}{2}\nu) + \frac{2\alpha}{\pi}\bigg]\Psi(\nu)$$

with mass parameter $\alpha$ depending on the quark mass.

Defining $Q(\nu) = \sinh(\frac{\pi\nu}{2})f(\nu)\Psi(\nu)$, where $f(\nu)$ encapsulates quark mass dependence, the equation is recast as a finite-difference Baxter type: $$Q(\nu+2i)+Q(\nu-2i)-2Q(\nu) = -\frac{4\pi\lambda}{f(\nu)} Q(\nu)$$ with the spectrum and wavefunctions inheriting the analytic properties and integrable structures of quantum spin chains. This integrable reformulation allows precise determination of analytic structure (branch points, eigenvalues) and spectral sums, and supports explicit computation for general quark masses.

4. Lattice Approaches and Meson Spectra

Applications of the ’t Hooft model as a lattice benchmark exploit the Twisted Eguchi-Kawai (TEK) volume reduction, allowing simulation on a single-site lattice in the large $N_c$ limit (Pérez et al., 2016). The lattice-regularized ’t Hooft model recovers the continuum spectrum (with Regge scaling $m_n^2 \sim n$ and $m_\pi^2\sim m_q$ at small quark mass) using a variety of fermion discretizations—Wilson, naive (staggered), and overlap. Discrepancies in observed masses (typically a few percent) can be systematically controlled by matching lattice and continuum definitions for quark mass and proper renormalization.

Furthermore, operator-based approaches project the operatorial transfer matrix framework (with a Bogoliubov vacuum) to an effective mesonic action through coherent-state path integrals. These techniques interpolate between canonical (operator) and functional (path-integral) representations, recover the gauge-theoretic vacuum structure, and describe both quadratic and quartic effective meson interactions (Caracciolo et al., 2018).

5. Entanglement, Anomalies, and Confinement Indicators

The entanglement structure of the ’t Hooft model exhibits striking simplifications at large $N$. Using the replica trick, the entanglement $c$-function of the model is found to be a sum of those for noninteracting massive scalars (each meson behaves as a pointlike degree of freedom for this measure, despite its extended, string-like structure) (Goykhman, 2015). The result encodes the transition from a free quark ($c_E\sim N/3$ for small intervals) to confined meson phases ($c_E\sim 1/3$ in the IR).

Anomalies in discrete symmetry realizations are also manifest in related ’t Hooft-type models. For example, analysis of staggered fermions and Kähler–Dirac fields on the lattice reveals perturbative U(1) anomalies broken to Z$_4$, and ’t Hooft anomalies for gauged discrete symmetries, matched only when the fermion content is appropriately doubled or higher (Catterall, 2022). These topological constraints are crucial for constructing lattice GUTs and ensuring consistency of mass generation mechanisms.

Disorder operators like the ’t Hooft loop and surface, both in continuum and on the lattice, serve as dual indicators to the Wilson loop for confinement and topological order. The relationship between interface tension, Casimir scaling, and the phase structure at finite temperature or with imaginary chemical potential is clarified through explicit analysis in both pure gauge and with dynamical quarks cases (Kashiwa et al., 2013, Shimazaki et al., 2020).

6. Extensions: Holographic Duals, Anomalies, and Effective Field Theories

The ’t Hooft model has been pivotal in motivating generalizations to higher-order and higher-dimensional holographic dualities, most notably in large-$N$ coset CFTs and higher-spin AdS$_3$ gravity (Ahn, 2011). The methods developed here have also been adapted to paper the structure of ’t Hooft anomalies in discrete gauge theories (Dijkgraaf–Witten theories), the role of non-Abelian group cohomology, and bulk–boundary correspondence via anomaly inflow (Müller et al., 2018).

In the context of the QCD phase diagram, the magnetic field dependence of the ’t Hooft determinant term in effective chiral models has been shown to be central for realizing inverse magnetic catalysis, with precise features for the behavior of constituent quark masses and meson spectra under external fields (Moreira et al., 2020).

A further direction is the investigation of mass decompositions (energy-momentum tensor analysis) in mesons, such as the pion, where the total light-front momentum resides entirely on the quarks, but the light-cone Hamiltonian energy splits between kinetic (quark) and “potential” (gluon-induced) parts, even in the deep infrared (Freese et al., 2022).

7. Impact, Limitations, and Future Directions

The ’t Hooft model provides a canonical analytic laboratory for testing both old and new methods in non-Abelian gauge theory—integrability, holography, lattice reduction, entanglement, anomaly matching, and effective field theory. It makes possible the explicit demonstration of dualities, spectral properties, and the emergence of topological order in confined, strongly coupled systems.

One limitation is the absence of genuine dynamical gluons, angular momentum, and baryons at leading order, making its phenomenological reach to full QCD indirect. However, many qualitative features (chiral symmetry breaking, the role of anomalies, spectral scaling, dual disorder operators) are believed to persist and inform the more complex $3+1$ dimensional theory.

Future research directions exploit the model’s integrable structure to address nonperturbative questions in topological string theory (Ambrosino et al., 2023), extend anomaly and topological analysis to condensed matter analogs, and further bridge the gap between lattice constructions and holography. Advanced studies of real-time evolution, nonzero density, and inhomogeneous backgrounds are anticipated to benefit from the analytic control the ’t Hooft model uniquely provides.