Switching Linear Dynamical System (SLDS)

• SLDS are state-space models that use discrete regimes to parameterize distinct linear dynamics, enabling the modeling of non-stationary time series.
• They incorporate regime-switching mechanisms, such as Markov chains and Bayesian nonparametric priors, for adaptive inference of multiple dynamic states.
• Extensions including explicit duration modeling and Pólya–Gamma augmentation enhance SLDS performance in applications like motion segmentation and neural data analysis.

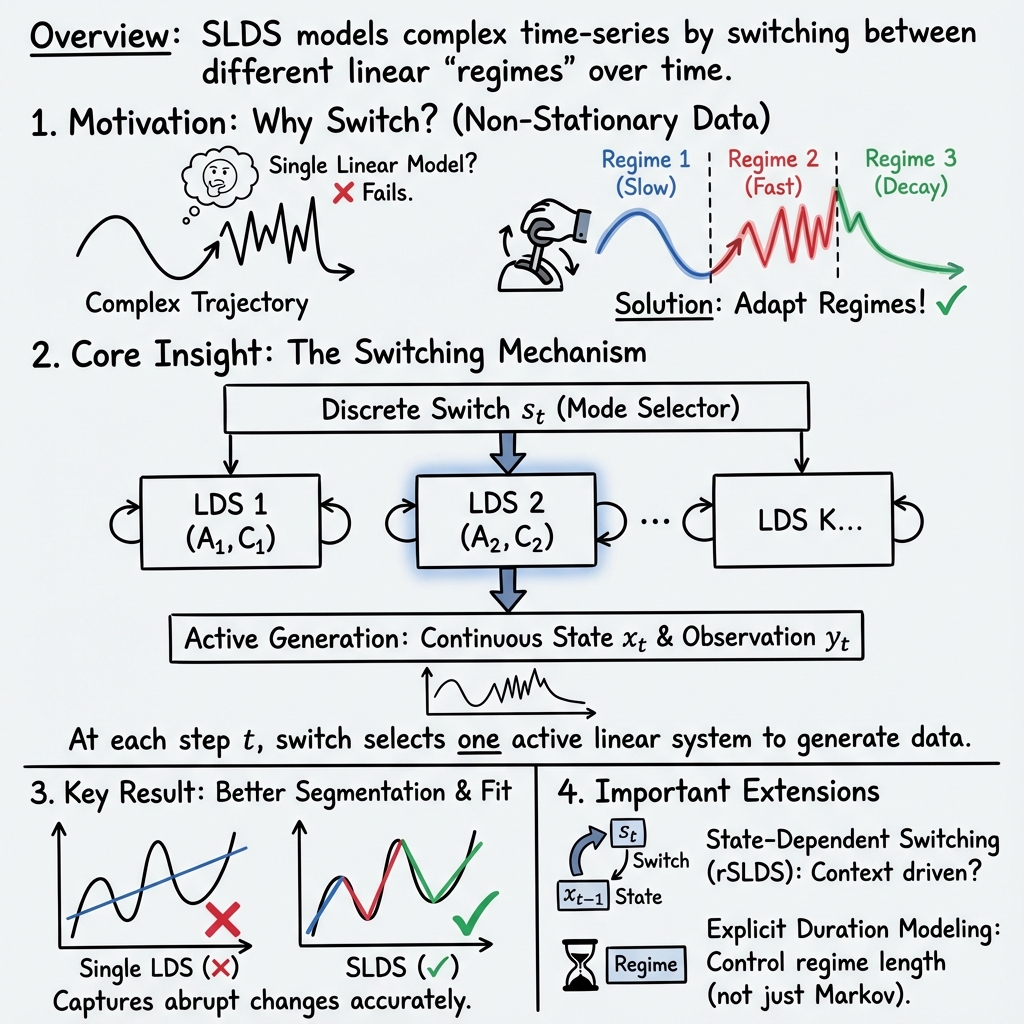
A Switching Linear Dynamical System (SLDS) is a stochastic state-space model in which the system dynamics are governed by a sequence of discrete “regimes,” with each regime specifying distinct linear dynamical equations for the evolution of latent continuous states and observations. Formally, at each time step, the discrete latent variable selects a mode (or regime) that parameterizes a linear dynamical system; both state and observation processes are then generated according to this mode’s parameters. The SLDS framework generalizes classical linear dynamical systems (e.g., Kalman filters) by incorporating non-stationarity and regime-switching, allowing rich modeling of time series with abrupt or contextually driven changes in dynamics.

1. Mathematical Formulation and Model Structure

At the core, an SLDS consists of the following generative process for each time step $t$:

• Discrete regime/latent mode: $s_t \in \{1, ..., K\}$.
• Continuous latent state: $x_t \in \mathbb{R}^n$.
• (Observed) output: $y_t \in \mathbb{R}^d$.

The model’s state evolution and observation equations are: $$\begin{aligned} &s_1 \sim \mathrm{Categorical}(\pi), \ &x_1 \sim \mathcal{N}(\mu_{s_1}, P_{s_1}), \ &y_1 \sim \mathcal{N}(C_{s_1} x_1, S_{s_1}), \ &\text{and for } t \ge 2:\ &s_t \sim P(s_t \mid s_{t-1}), \ &x_t = A_{s_t} x_{t-1} + a_{s_t} + \varepsilon_t,\quad \varepsilon_t \sim \mathcal{N}(0, Q_{s_t}), \ &y_t = C_{s_t} x_t + c_{s_t} + \eta_t, \quad \eta_t \sim \mathcal{N}(0, S_{s_t}). \end{aligned}$$

In the canonical SLDS, the mode sequence $\{s_t\}$ is a Markov chain with transition matrix $\{P(s_t | s_{t-1})\}$. The parameters $\{A_k, a_k, Q_k, C_k, c_k, S_k\}_{k=1}^K$ define mode-specific dynamics and emissions. Extensions allow richer dependencies, such as state-dependent switching or explicit duration modeling.

2. Regime-Switching, Nonparametric Priors, and Duration Modeling

Regime-Switching with Classical and Bayesian Nonparametric Priors

Early SLDS formulations assumed a fixed $K$ and Markovian switching. In Bayesian nonparametric approaches, a Hierarchical Dirichlet Process (HDP) prior is placed over mode transitions, allowing an (in principle) infinite number of possible regimes. The “sticky HDP-HMM” variant introduces a self-transition parameter $\kappa$, biasing mode persistence: $$\pi_j \sim \mathrm{DP}(\alpha+\kappa, (\alpha \beta + \kappa \delta_j)/(\alpha+\kappa)),$$ where $\beta$ is a random measure from the GEM process and $\delta_j$ is a Dirac at $j$ (Fox et al., 2010). This allows models to adaptively learn the number and identity of dynamical regimes from data.

Explicit Duration Modeling and State-Dependent Switching

The REDSLDS model augments SLDS by introducing an explicit duration variable $d_t$ tracked at each step and a switching mechanism in which $p(s_t | s_{t-1}, d_{t-1}, x_{t-1})$ and $p(d_t | s_t, d_{t-1}, x_{t-1})$ depend simultaneously on past discrete and continuous states (Słupiński et al., 6 Nov 2024). The structure is: $$p(y_{1:T}, x_{1:T}, s_{1:T}, d_{1:T}) = \text{[initial terms]} \prod_{t=2}^T [p(s_t|s_{t-1}, d_{t-1}, x_{t-1}) p(d_t|s_t, d_{t-1}, x_{t-1}) \dots ]$$ Such explicit duration modeling enforces non-geometric state durations and persistent regimes, crucial for realistic segmentation.

3. Inference Algorithms and Pólya–Gamma Augmentation

Parameter estimation and inference in SLDS are computationally challenging due to the exponentially many mode sequences and the coupling between discrete and continuous variables. Well-established algorithms include:

• Blocked Gibbs Sampling: Alternates sampling of entire mode and state sequences; uses forward–backward algorithms for discrete state sequences and Kalman filtering/smoothing for continuous trajectories (Fox et al., 2010).
• Variational Inference: Mean-field factorization enables tractable approximation, with auxiliary variables allowing tractable updates for both discrete and continuous states (Basbug et al., 2015).
• Pólya–Gamma Augmentation: For state-dependent switching (e.g., in rSLDS, TrSLDS, REDSLDS), logistic stick–breaking transition models complicate inference. Introducing Pólya–Gamma auxiliary variables $\omega \sim PG(b, 0)$ transforms the logistic term into a (conditionally) Gaussian form, yielding closed-form conditional updates for regression weights in the transition and duration distributions (Linderman et al., 2016, Nassar et al., 2018, Słupiński et al., 6 Nov 2024). The key identity is: $$\frac{(e^{\psi})^a}{(1+e^{\psi})^b} = 2^{-b} e^{\kappa \psi} \int_0^\infty \exp\big(-\frac{1}{2}\omega \psi^2\big) p_{PG}(\omega|b, 0)d\omega, \quad \text{where} \ \kappa = a - b/2.$$

Forward–backward message passing incorporates Kalman information filtering for latent state inference and explicit blockage for the joint discrete variables, while stick–breaking logistic regressions are fit via augmented conditionally conjugate Bayesian updates.

4. Extensions: State-Dependent and Hierarchical Regimes

Recurrent Switching (rSLDS, TrSLDS, REDSLDS)

Recurrent SLDSs (rSLDS) allow the mode transition probabilities to depend on the previous continuous state: $$p(s_{t+1} | s_t, x_t) = \pi_{SB}(\nu_{t+1}), \quad \nu_{t+1} = R_{s_t} x_t + r_{s_t}$$ (Linderman et al., 2016). This captures context-dependent or threshold-triggered switches (e.g., spiking neurons, behavioral transitions).

Tree-Structured rSLDS (TrSLDS) (Nassar et al., 2018) hierarchically partitions latent space through stick–breaking at each tree node, yielding a multi-scale description that interpolates between coarse and fine regime granularity, with hierarchical priors ensuring parameter sharing among nested regimes.

Explicit Duration and REDSLDS

Explicit modeling of regime duration via a latent variable $d_t$ resolves the unrealistic geometric waiting times inherent in Markov switching. In REDSLDS (Słupiński et al., 6 Nov 2024), the duration distribution, as well as regime transitions, depend on $x_{t-1}$, and both are realized via stick-breaking logistic regressions combined with Pólya–Gamma augmentation. For $d_{t-1} = 1$, a new state $s_t$ and duration $d_t$ are sampled as: $$p(s_t | s_{t-1}, x_{t-1}) = \pi_{SB}(R^S_{s_{t-1}} x_{t-1} + r^S_{s_{t-1}}); \quad p(d_t | s_t, x_{t-1}) = \pi_{SB}(R^D_{s_t} x_{t-1} + r^D_{s_t})$$ with Dirac delta distributions enforcing persistence when $d_{t-1} > 1$.

5. Applications and Empirical Performance

SLDS and its extensions have demonstrated utility across diverse settings:

• Motion and Trajectory Segmentation: Automatic discovery and segmentation of movement primitives from demonstrations (robotics, vehicle, animal trajectories), using HDP-sticky-SLDS and Gibbs/variational inference (Fox et al., 2010, Sieb et al., 2018).
• Physiological and Neural Data Analysis: Discriminative SLDS (DSLDS) tracks patient state in ICUs, segmenting real and artifactual events, leveraging discriminative classifiers for the switch variable combined with classical LDS filtering (Georgatzis et al., 2015). Tree-structured and state-dependent SLDS models extract coherent neural state-space partitions and are capable of identifying switching driven by underlying latent factors (Nassar et al., 2018).
• Human Activity Recognition: Sticky HDP-SLDS accurately classifies activities from accelerometer data, using the nonparametric, sticky regime prior and variational inference for scalability (Basbug et al., 2015).
• LLM Reasoning: The reasoning dynamics of transformer LMs have been analyzed via SLDS on rank-40 projections of hidden states, with four learned regimes corresponding to phases such as systematic decomposition or “misaligned” states (Carson et al., 4 Jun 2025).
• Narrative Generation: SLDS-based models induce sentence-level latent state trajectories driven by high-level narrative regimes (e.g., sentiment), providing explicit control and interpretable interpolations in text-generation tasks (Weber et al., 2020).
• Physical and Imaging Systems: Patch-based SLDS estimator frameworks segment spatiotemporal data into locally linear regions governed by decoupled SLDS patches for real-time dynamic imaging (Karimi et al., 2021).

In each case, the ability to handle non-stationary dynamics, context-dependent transitions, persistent states, and high-dimensional signal evolution highlights the versatility of the SLDS framework and its extensions.

6. Theoretical and Computational Properties

• Identifiability and Parsimony: Automatic relevance determination (ARD) and nonparametric priors ensure over-specified models are regularized towards parsimony, turning off unnecessary states or orders (Fox et al., 2010).
• Computation: Blocked Gibbs or variational inference using message passing on LDS/HMM structures, Pólya–Gamma augmentation for non-Gaussian transitions, and tree-based or neural network parameter sharing allows efficient estimation in high dimensions (Linderman et al., 2016, Nassar et al., 2018).
• Handling Irregularity: Continuous-time extensions (using forward–backward solutions for stochastic SDEs) naturally accommodate irregularly sampled and partially missing data, crucial for scientific settings such as gene regulatory networks (Halmos et al., 2023).

7. Impact, Limitations, and Future Directions

SLDS methods provide interpretable, modular decompositions of complex time-series, uncovering regimes and their driving signatures without requiring strong a priori knowledge of the number of modes. Hierarchical and state-dependent variants can model multi-scale and context-dependent transitions while explicit-duration models enforce realistic regime persistence, improving segmentation performance and robustness—especially in short, fragmented observations (Słupiński et al., 6 Nov 2024).

Ongoing research addresses scaling SLDS frameworks to very high-dimensional settings (e.g., large neural datasets, natural language processing), relaxing linearity via locally linear or neural parametric extensions (“locally switched nonlinear systems”), and coupling with deep learning-based observation models. Efficient, solver-free geometric algebra algorithms for control and boundary problems, and robust model selection techniques via graph-based clustering, further extend the SLDS methodology (Derevianko et al., 2021, Karimi et al., 2020).

Across scientific and engineering domains, the modern SLDS and its extensions serve as a foundation for principled, interpretable modeling of temporally structured, non-stationary, or regime-switching dynamical phenomena.