Scrooge Ensemble in Quantum Information Theory

• Scrooge ensemble is defined as the unique ensemble of pure states that minimizes accessible information while preserving a fixed density matrix, serving as a fundamental tool in quantum statistical mechanics.
• It is constructed via a distorted Haar measure and emerges in many-body quantum systems through mechanisms such as chaotic dynamics and subsystem projection.
• Extensions to continuous-variable Gaussian systems reveal universal behaviors that inform quantum tomography, benchmarking, and thermalization studies.

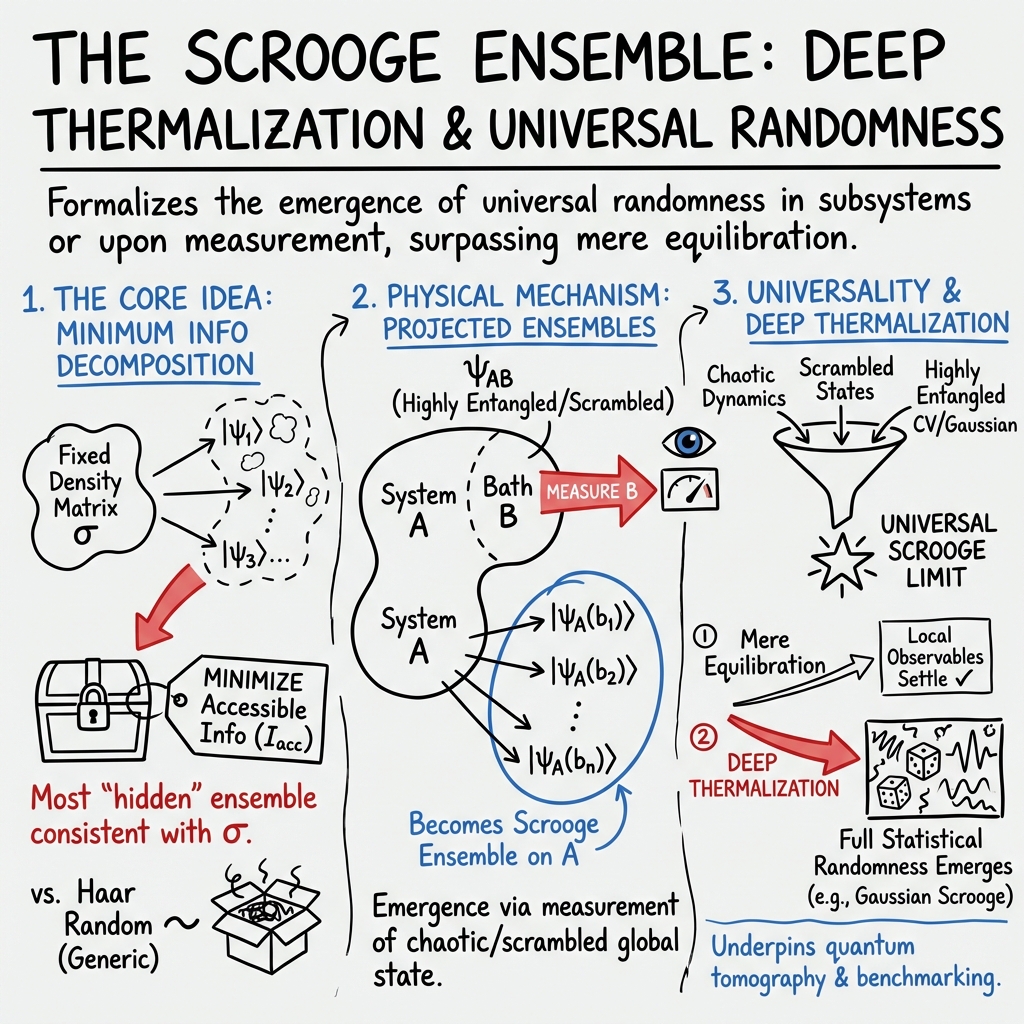
The Scrooge ensemble is a fundamental construct in quantum statistical mechanics and quantum information theory, representing a maximally entropic, information-minimizing ensemble of pure states consistent with a fixed density matrix. Broadly, Scrooge ensembles formalize the notion of deep thermalization: the emergence of universal randomness in subsystems or upon measurement, surpassing the mere equilibration of local observable statistics. Recent work generalizes the concept from discrete-variable systems to continuous-variable (CV) Gaussian systems, elucidating its operational significance, mathematical characterization, physical mechanisms of emergence, and implications for many-body dynamics, benchmarking, and quantum tomography (Liu et al., 2024, Manna et al., 3 Jan 2025, McGinley et al., 21 Nov 2025, Mok et al., 1 Jan 2026, Wootters, 2018).

1. Mathematical Definition and Information-Theoretic Properties

The Scrooge ensemble is defined, for a Hilbert space $\mathcal{H}$ of dimension $D$ and target density matrix $\sigma$, as the unique ensemble of pure states $\{p(\psi), |\psi\rangle\}$ that (i) yields $\sigma$ as its first moment ($$\int p(\psi)|\psi\rangle\langle\psi| d\psi = \sigma$$), and (ii) minimizes the accessible information $I_\mathrm{acc}(\mathcal{E})$ (Wootters, 2018, Mok et al., 1 Jan 2026). This information-theoretic minimality sets the Scrooge ensemble apart from Haar or other random-state ensembles.

Formally, the ensemble is constructed via a "distorted" Haar measure: $$p(\psi) d\psi = D\, \langle\phi|\sigma|\phi\rangle d\phi,\qquad |\psi\rangle = \sigma^{1/2} |\phi\rangle / \|\sigma^{1/2}|\phi\rangle\|$$ with $|\phi\rangle$ Haar-random. This distortion pushes the measure to reside on the boundary of distinguishable states while saturating the first-moment constraint.

For the $k$-th moment, the operator is

$$\rho^{(k)}_\mathrm{Scrooge}(\sigma) = D \int_{\mathrm{Haar}} \left(\sigma^{1/2}|\phi\rangle\langle\phi|\sigma^{1/2}\right)^{\otimes k} \langle\phi|\sigma|\phi\rangle^{1-k}\, d\phi$$

Minimization of accessible information makes the Scrooge ensemble the unique solution to the maximum-entropy decomposition problem.

2. Scrooge Ensembles in Quantum Many-Body Systems

Scrooge ensembles are realized in physical systems through the process of projecting onto subsystems after measurement or via the dynamics of strongly chaotic, ergodic Hamiltonians. In projected ensembles, where part of a bipartite system $A\cup B$ is measured, the post-measurement pure-state outcomes form an ensemble on subsystem $A$ (Mok et al., 1 Jan 2026, Manna et al., 3 Jan 2025): $$E_\mathrm{PE}(\psi_{AB}) = \{p(b), |\psi_A(b)\rangle\}_{b \in S_B}$$ with $$|\psi_A(b)\rangle \propto (I_A \otimes \langle b|)\psi_{AB}$$.

If the global state or measurement basis is sufficiently scrambled or chaotic, convergence to the Scrooge ensemble on $A$ is observed in the thermodynamic and late-time limits (McGinley et al., 21 Nov 2025, Manna et al., 3 Jan 2025). Under generic conditions, the projected ensemble's $k$-th moments coincide with those of the Scrooge ensemble built from the reduced density matrix $\rho_A$.

The Scrooge ensemble formalizes the statistical property that subsystems exhibit exponential concentration in local observables, while retaining global fluctuations analogous to Porter-Thomas statistics. This separation is robust in highly entangled, complex global states and underpins the notion of deep thermalization (McGinley et al., 21 Nov 2025).

3. Gaussian Scrooge Distribution in Continuous-Variable Systems

Recent work extends the Scrooge ensemble to bosonic Gaussian states in CV systems (Liu et al., 2024). Here, one studies an $n$-mode pure, zero-mean Gaussian state, partitions into $A$ (system) and $B$ (bath), and performs Gaussian measurements on $B$, inducing a projected ensemble on $A$. The covariance matrix decomposes as

$$V = \begin{pmatrix} V_A & V_{AB} \ V_{AB}^T & V_B \end{pmatrix}$$

and the projected ensemble is comprised of pure BGSs with affine-distributed first moments.

A universal limit emerges: for highly entangled global states (random Gaussian states, deep linear circuits, etc.), in the thermodynamic limit $n\to\infty$ and fixed particle-density $\nu$, the projected ensemble becomes the Gaussian Scrooge distribution—a family of coherent states with

$$\widetilde V_A \rightarrow \mathbb{I}_{2k},\qquad \Sigma_A \rightarrow \nu\, \mathbb{I}_{2k}$$

and complex amplitudes $\boldsymbol{\alpha}$ distributed isotropically as

$$P(\boldsymbol{\alpha}) = \frac{1}{(\pi\nu)^k} \exp\left(-\frac{\|\boldsymbol{\alpha}\|^2}{\nu}\right)$$

This universal ensemble is independent of the measurement basis and uniquely minimizes accessible information, consistent with a generalized maximum-entropy principle.

4. Physical Mechanisms and Resource Requirements for Emergence

Rigorous results establish three distinct physical mechanisms for the generation of Scrooge ensembles as approximate $k$-designs (Mok et al., 1 Jan 2026):

• Global chaotic dynamics: Temporal random-phase ensembles of time-evolved states under chaotic Hamiltonians converge to Scrooge ensembles on the diagonal density.
• Scrambled global states: Measurement on part of a highly scrambled global Scrooge $2k$-design induces a local Scrooge $k$-design in the unmeasured subsystem.
• Scrambled measurement basis: For any fixed entangled state, applying a Haar-random (or approximate $2k$-design) unitary to the bath before measurement ensures the projected ensemble on the system becomes a Scrooge $k$-design.

Numerical simulations corroborate these mechanisms and demonstrate that coherence, entanglement, "magic" (non-stabilizerness), and information scrambling are strictly necessary resources.

5. Analytical Representations, k-Designs, and Convergence

The moment calculus for Scrooge ensembles allows efficient evaluation of statistical properties. For highly mixed (large min-entropy) backgrounds, moments are tightly approximated by explicit formulas (McGinley et al., 21 Nov 2025): $$\chi^{(k)}_{\mathcal{S}_\rho} \approx_{rel} \rho^{\otimes k}\sum_{\pi\in S_k} \pi$$ with error bounded by $$\delta_{\rho,k} = O(k^2 2^{-\frac{1}{2}S_\infty(\rho)})$$.

Definitions of exact and approximate $k$-designs are given, quantifying ensemble proximity in trace norm or relative error (Mok et al., 1 Jan 2026): $$\frac{1}{2}\|\rho_\mathcal{E}^{(k)} - \rho_\mathrm{Scrooge}^{(k)}(\sigma)\|_1 \leq \epsilon_\mathrm{add}$$ and

$$(1-\epsilon_\mathrm{rel})\,\rho_\mathrm{Scrooge}^{(k)}(\sigma) \preceq \rho_\mathcal{E}^{(k)} \preceq (1+\epsilon_\mathrm{rel})\,\rho_\mathrm{Scrooge}^{(k)}(\sigma)$$

These statements underlie proofs of deep thermalization and universal emergence in the large-system and long-time limits.

6. Classical Analogue, Subentropy, and Maximal Entropy Principle

The Scrooge ensemble is intimately connected to the quantum subentropy $Q(\rho)$, the minimal accessible information achievable by any pure-state decomposition of a mixed state $\rho$ (Wootters, 2018). The ensemble's marginal probability density over the simplex of amplitudes for eigenvalue vector $\vec{\lambda}$ is: $$\sigma(x) = \frac{n!}{\lambda_1\cdots\lambda_n} \left(\sum_j \frac{x_j}{\lambda_j}\right)^{-(n+1)}$$ and the accessible information of any measurement achieves $Q(\rho)$, independent of the basis. The construction admits a classical analogue by embedding in a higher-dimensional amplitude space and coarse-graining, reinforcing the extremal information-theoretic principle that links quantum and classical entropy optimization.

7. Applications and Physical Relevance

Scrooge ensembles underpin modern approaches to benchmarking, tomography, and verification for quantum devices in realistic, constrained settings (finite energy, conservation laws) (McGinley et al., 21 Nov 2025, Mok et al., 1 Jan 2026). The fine-grained prediction of output statistics, including PT-like fluctuations and mutual information quantization, has implications for cross-entropy diagnostics and sampling hardness. In CV systems, the Gaussian Scrooge distribution may enable optimal random-state generation for shadow protocols or cryptographic applications (Liu et al., 2024).

The universality and minimal-information property of Scrooge ensembles places deep thermalization and randomization on a rigorous footing, bridging random-matrix theory, integrable and ergodic dynamics, and quantum information—theoretical unification supported by analytical results and extensive numerics.