One-Layer Transformers

• One-layer transformers are a minimalist architecture that uses a single encoder or decoder block with multi-head self-attention and position-wise feed-forward networks for efficient sequence modeling.
• Theoretical analyses show they are universal approximators and can implement algorithms like nearest neighbor classification and Bayesian denoising under specific parameterizations.
• Practical implementations enable rapid prototyping in tasks such as memorization, graph representation learning, and denoising, though they face limits in multi-step reasoning and complex communication tasks.

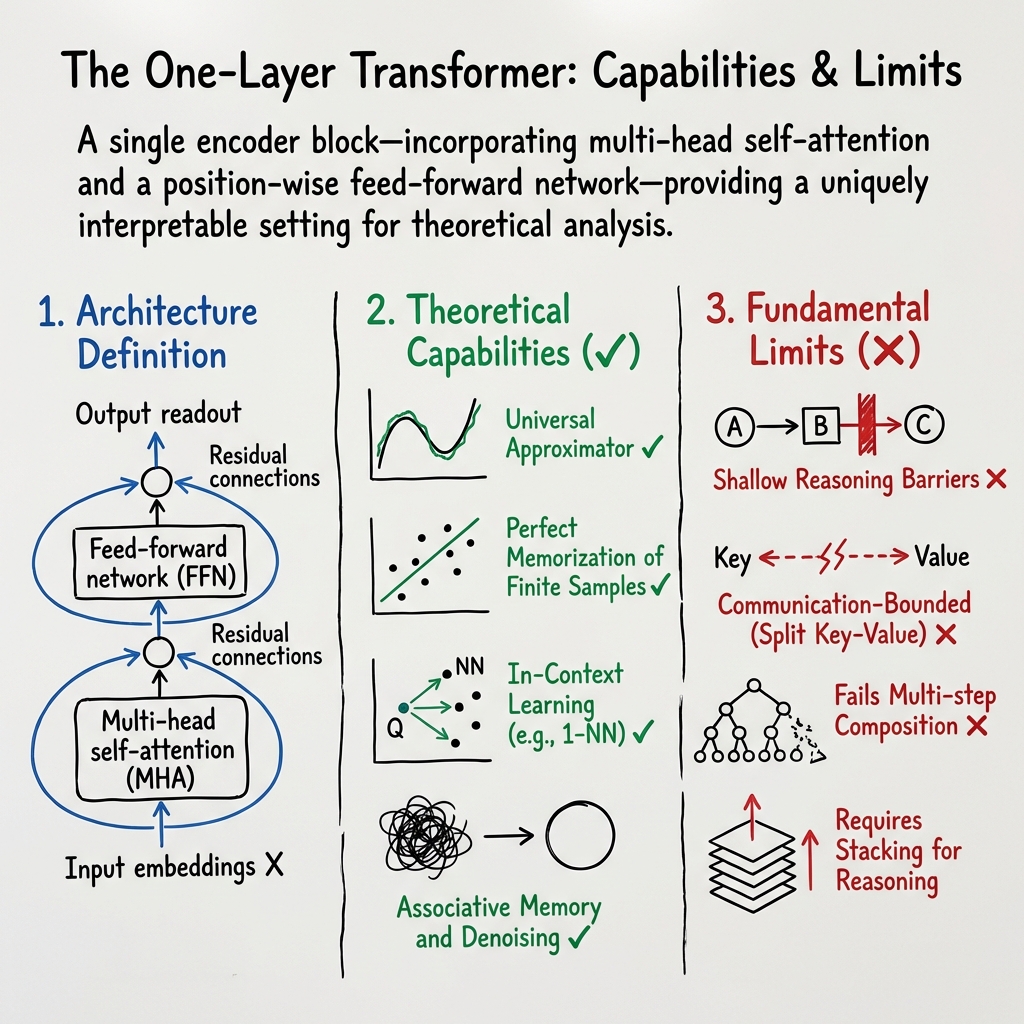
A one-layer transformer is a variant of the standard transformer architecture that consists of a single encoder or decoder block—incorporating multi-head self-attention and a position-wise feed-forward network—along with optional layer normalization and residual connections. This design represents the shallowest possible instantiation of the transformer model, providing a uniquely interpretable setting for theoretical analysis, model efficiency studies, and functional capacity characterization. Extensive recent research has elucidated the capabilities, fundamental limits, and practical implications of one-layer transformers across diverse machine learning domains.

1. Definition and Architecture

A canonical one-layer transformer consists of the following elements:

• Input embeddings $\mathbf{X} \in \mathbb{R}^{n \times d}$ (token and positional).
• Multi-head self-attention (MHA): For $h$ heads, each computes

$$\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d_k}}\right)\mathbf{V}$$

where $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ are learned linear projections of $\mathbf{X}$.

• Feed-forward network (FFN): Position-wise, typically two layers with a nonlinearity (e.g., ReLU).
• Residual connections and layer normalization (optional, but does not affect expressivity results).
• Output readout or prediction head.

Parameterization can include standard or low-rank weight matrices, and variants are studied both for full (softmax) and linear (kernel) attention, as well as extensions to wide-head regimes ($h \gg 1$) (Gumaan, 11 Jul 2025, Brown et al., 2022, Shen et al., 2021, Kajitsuka et al., 2023).

2. Theoretical Expressivity and Universal Approximation

Recent theoretical advances have established the following for one-layer transformers:

• Universal Approximation Theorems: A single-layer transformer (self-attention and ReLU-FFN) is a universal approximator of continuous sequence-to-sequence maps on compact domains. For every continuous $f$, for any $\varepsilon>0$, there exists a choice of heads, widths, and weights so the transformer $T$ realizes $$\sup_{\mathbf{X}}\|T(\mathbf{X})-f(\mathbf{X})\|_\infty<\varepsilon$$ (Gumaan, 11 Jul 2025).
• Softmax/Boltzmann Operator: The softmax aggregation induces a powerful set-indexed "context id" via the Boltzmann operator, which can separate finite samples or describe piecewise-constant selectors over the input space (Kajitsuka et al., 2023).
• Permutation Equivariance: With suitable parameterization, a one-layer (or one-head with two FFN layers) transformer is a universal approximator of continuous permutation-equivariant functions (Kajitsuka et al., 2023).
• Memorization of Finite Samples: Given separated token embeddings or carefully designed position encodings, a one-layer transformer can perfectly memorize (i.e., interpolate) arbitrary finite datasets (Kajitsuka et al., 2023, Chen et al., 2024).
• Limits and Barriers: The universality construction is non-constructive in the sense that large width, many heads, or large weights may be required, and there is no guarantee that gradient-based methods will find such solutions in practical settings (Gumaan, 11 Jul 2025, Chen et al., 2024).

3. Algorithmic Capabilities, Computation, and Limitations

Single-layer transformers can implement several classes of algorithms, but also exhibit sharp limitations:

• Algorithmic In-Context Learning: On certain stylized datasets, a one-layer transformer trained on in-context regression provably learns to perform a single step of gradient descent (GD) or preconditioned GD, coinciding with Bayes-optimal learning under Gaussian assumptions (Mahankali et al., 2023, Nguyen et al., 21 May 2025). For next-token prediction, provably Bayes-optimal solutions are possible, with convergence at a linear rate under normalized gradient descent (Nguyen et al., 21 May 2025).
• One-Nearest Neighbor: Explicit construction and convergence analysis show that a one-layer softmax-attention transformer can learn to implement the 1–NN classifier via a nonconvex loss, provided initialization is appropriately designed (Li et al., 2024).
• Associative Memory and Denoising: In a Bayesian denoising context, a one-layer transformer equates to a single gradient update on a dense associative memory (Hopfield) energy, providing the Bayes-optimal context-based denoiser when context size grows (Smart et al., 7 Feb 2025).
• Graph Representation Learning: In graph domains, one-layer hybrid layers (attention + GNN-like propagation) can express the outcome of arbitrary-depth message passing by a suitable refactorization, providing explicit architectural collapse and $O(N+E)$ complexity for large ($N \gg 10^6$) graphs (Wu et al., 2024).
• Limits in Function Computation: One-layer transformers are communication-bounded in look-up or functional evaluation tasks where key-value binding spans multiple positions. Given polylogarithmic parameter budget, function evaluation is possible only when key and value are co-located in tokens or sequence position; otherwise, superlinear ($\Omega(n\log n)$) resources or depth-2 models are needed (Strobl et al., 28 Mar 2025). Analogous lower bounds appear for the induction-heads task (Sanford et al., 2024).
• Shallow Reasoning Barriers: For sequence learning, a single attention layer can realize only memorization (direct mapping of sequences) but not multi-step reasoning, template generalization, or context-dependent inference, which require stacking multiple layers to decompose compositional operations (Chen et al., 2024).

Area	What One Layer Achieves	Limitation versus Depth
Memorization	Perfect finite sample fitting	–
1-NN Algorithms	Provable convergence to in-context 1-NN	–
Gradient Step	Implements first-step GD on linear tasks	Not higher-order or iterative
Reasoning Tasks	Only one-step copy/parse possible	No multi-hop reasoning
Communication	Functional evaluation if key=token pos	Fails for split key-value, needs depth
Induction Heads	Requires $\Omega(n)$ size	Two layers suffice with $O(\log n)$

4. Optimization Behavior, Low-Rank/Sparse Properties, and Architecture Variants

Analyses of optimization and architectural properties have yielded the following insights:

• Gradient Dynamics: In pattern-based data models, the total gradient updates of a one-layer transformer under SGD are low-rank, with rank at most the number of label-relevant patterns (substantially below parameter dimension if only a few patterns matter), and changes are nearly orthogonal to label-irrelevant features (Li et al., 2024).
• Magnitude-Based Pruning: A fraction of output neurons converge to negligible row norms; magnitude-based pruning can eliminate these inactive units with minor test-time performance degradation and significant computational savings. Retaining only neurons aligned with label-relevant patterns suffices for generalization (Li et al., 2024).
• Sparsification and Lottery Tickets: Application of binary masks over fixed random weights (without training) can reveal subnetworks in one-layer transformers that match or approach trained performance on machine translation, retrieving >98% of the BLEU score of a trained one-layer model and >92% of a trained 6-layer model (with fixed pretrained embeddings). Varying random initialization type affects achievable BLEU, with Kaiming or Xavier uniform best (Shen et al., 2021).
• Wide-Attention versus Depth: Holding total head count fixed, making the single layer extremely wide ($H \gg 1$) lets one-layer transformers match or slightly surpass deeper ($L>1$) models in efficiency and accuracy for small-to-medium NLP tasks, while being more interpretable and resource-efficient (e.g., 3.1$\times$ faster CPU inference on byte-level IMDb vs. deep, half the size) (Brown et al., 2022). This is less effective for domains relying on intermediate pooling or hierarchy (e.g., vision transformers).
• Attention Mechanism Variants: Performance is robust across many attention mechanisms (dot-product, BigBird, Performer, etc.) provided width is saturated (Brown et al., 2022).

5. Inductive Bias, Generalization, and Interpretability

Key results clarify the generalization and interpretability of one-layer transformers:

• Generalization in In-Context Tasks: For next-token prediction, reparameterized one-layer models trained with NGD provably generalize to out-of-vocabulary tokens, with the convergence rate and error quantifiable in terms of steps and sample size (Nguyen et al., 21 May 2025).
• Layer Specialization: During training, attention heads specialize to context-sensitive features, while feed-forward heads can partition high-level categories (e.g., noise), matching empirical findings in deep LLMs (Nguyen et al., 21 May 2025).
• Interpretability: The entire computation in one layer (especially in wide models) is directly inspectable, as each head's contribution is explicit and not compounded across layers, allowing detailed tracing of attention focus and decision-making (Brown et al., 2022).
• Limits of Generalization: In synthetic and compositional settings, the one-layer model generalizes only to the extent that the task decomposes into a single linear attention step; otherwise, further depth is required for hierarchical or multi-stage reasoners (Chen et al., 2024).

6. Practical Implications and Model Design Considerations

• Rapid Prototyping and Parameter-Efficiency: For tasks where a single "step" of attention suffices—memorization, nearest-neighbor lookup, denoising, and tasks reducible to sparse context matching—one-layer transformers provide parameter-efficient, interpretable, and low-latency solutions (Li et al., 2024, Brown et al., 2022, Gumaan, 11 Jul 2025, Strobl et al., 28 Mar 2025).
• Random-Feature and Sparsity Methods: Randomly initialized one-layer models, followed by mask-based subnetwork search, offer a paradigm for constructing competitive translation systems without extensive gradient-based training, relating to "lottery ticket" and "random kitchen sinks" ideas (Shen et al., 2021).
• Graph Modeling at Scale: The SGFormer demonstrates that for graph learning, one hybrid layer can achieve depth-equivalent expressivity and supports efficient scaling to web-scale graphs (up to $10^8$ nodes), suggesting deep propagation may be unnecessary for many tasks (Wu et al., 2024).

7. Open Challenges and Future Directions

• Communication Complexity Barriers: Communication complexity lower bounds indicate exponential bottlenecks for certain routing and induction tasks in a single layer, which are surmounted by stacking two or more layers or by augmenting with recurrence or memory modules (Sanford et al., 2024, Strobl et al., 28 Mar 2025).
• Learnability Versus Capacity: While universal approximation theorems guarantee representational sufficiency, optimization via gradient descent in practice may remain trapped in poor minima without engineered initializations or parameterizations, especially as model size grows (Gumaan, 11 Jul 2025, Li et al., 2024).
• Extensions to Richer Architectures: Future work seeks to:
  • Develop mask-search methods beyond greedy or brute-force for random-feature subnetworks.
  • Analyze the emergence and compositionality of inductive biases in deeper or multi-block transformers.
  • Extend analytical frameworks to transformers with nonlinear or kernelized attention, or to domains beyond language (vision, structure, multimodal).
  • Quantify the emergence of Hopfield-type or reservoir computing capabilities in single-layer settings, and their role in few-shot/adaptive inference.

In sum, one-layer transformers are remarkably expressive for memorization, simple associative tasks, denoising, and graph representation—under precisely characterized conditions—but encounter decisive barriers with multi-step reasoning, memory routing, or function composition, highlighting both the strengths and the necessary limitations of architectural minimalism (Gumaan, 11 Jul 2025, Kajitsuka et al., 2023, Brown et al., 2022, Shen et al., 2021, Sanford et al., 2024, Nguyen et al., 21 May 2025, Li et al., 2024, Chen et al., 2024, Strobl et al., 28 Mar 2025, Li et al., 2024, Smart et al., 7 Feb 2025, Wu et al., 2024).