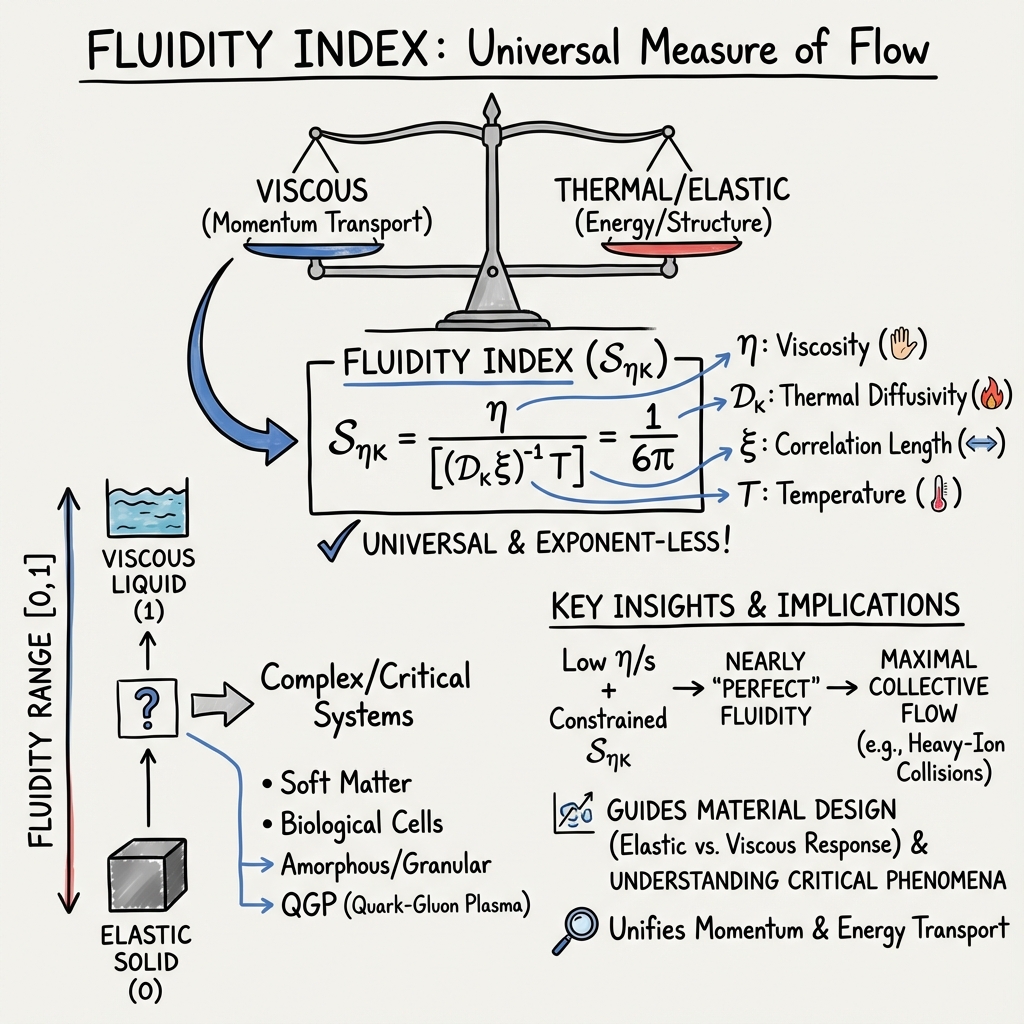
Fluidity Index: Quantifying Flow & Deformation

• Fluidity index is a dimensionless measure that quantifies a medium’s ability to flow by balancing viscous forces with thermal and elastic responses.
• It is derived from measurable parameters such as shear viscosity, thermal diffusivity, and correlation length, often using spectral analysis of Rayleigh peaks.
• Its universal, exponent-less formulation (e.g., 1/6π) enables comparative analysis across systems ranging from quark–gluon plasma to biological cells.

Fluidity-Index denotes the quantification of a medium’s ability to flow or undergo deformation in response to applied stresses. In contemporary physical, chemical, and biological contexts, and increasingly in materials science and computational modeling, the “fluidity index” is both a conceptual and mathematically precise parameter reflecting the balance—and often the competition—between viscous (momentum transport) and thermal or elastic (energy transport, structural rearrangement) mechanisms that control flow behavior. While its precise definition is domain dependent, in all systems it encodes the characteristic dynamical or structural “distance” between idealized perfectly elastic or perfectly viscous response and the real, often complex, dynamics observable in critical phenomena, disordered and living matter, advanced manufacturing, and information systems.

1. Fundamental Measures and Definitions

In classical fluids, the archetypal metric for fluidity is the inverse of shear viscosity, η⁻¹. More generally—and especially in near-critical or complex fluids—the “fluidity index” can be expressed as a dimensionless ratio involving viscosity, diffusivity, correlation length, and temperature.

A central, exponent-less and universal measure of fluidity, as justified by mode-mode coupling theory, is

$$\mathcal{S}_{\eta\kappa} = \frac{\eta}{[(\mathcal{D}_\kappa \xi)^{-1} T]} = \frac{1}{6\pi}.$$

Here:

• η is shear viscosity (dynamical coefficient),
• $\mathcal{D}_\kappa$ is thermal diffusivity (with $\mathcal{D}_\kappa = \kappa/(n_0 \widetilde{C}_P)$, κ: thermal conductivity, $n_0$: density, $\widetilde{C}_P$: specific heat),
• ξ is the correlation length,
• T is the temperature.

No non-universal critical exponents enter this measure, hence it is “exponent-less” as opposed to classical η/s or similar ratios (Abir et al., 2010). In soft matter contexts or in viscoelastic biological systems, fluidity is frequently extracted as a nondimensional parameter in the range [0,1], representing a position between elastic solid (0) and viscous liquid (1). In amorphous and granular media, it is operationalized via f = $\dot{\gamma}/\sigma$ (inverse effective viscosity) or, equivalently, in terms of plastic event or rearrangement rates.

2. Spectral, Dynamical, and Structural Basis

Fluidity measures often derive from spectral analysis of fluctuations or transport, e.g., via the width (half-width at half-maximum) of the Rayleigh peak in density fluctuation spectra:

$\Gamma_R = \mathcal{D}_\kappa q^2,$

where q is the scattering wavevector and $\mathcal{D}_\kappa$ is thermal diffusivity. Experimental dimensionless combinations such as

$\Gamma^* = \frac{6\pi \eta \Gamma_R}{T q^3}$

collapse to unity at critical points or in nonhydrodynamic regimes (qξ ≳ 1), demonstrating universality. This underlies the emergence of $\mathcal{S}_{\eta\kappa}$ above, since when $\Gamma^* \to 1$, fluidity cannot be further reduced to system-dependent scaling laws but is rather governed by the interplay of hydrodynamic and thermal relaxation channels.

Critically, identification of fluidity indices using only viscosity and entropy density (e.g., η/s) is insufficient, as neither carry robust critical divergences, but their ratios (via underlying diffusive processes) can inherit effective critical exponents, particularly in contexts like the quark–gluon plasma (QGP) (Abir et al., 2010). Thus, the fluidity index provides a more intrinsic and dynamical link—uniting momentum and energy transport, spectral features, and the microphysics of correlation lengths—across hydrodynamic regimes.

3. Universality, Criticality, and Applicability

The aforementioned dimensionless fluidity measures exhibit remarkable cross-system universality:

• Universality extends over molecular and atomic fluids undergoing liquid–gas transitions, both in hydrodynamic and fluctuation-dominated (critical) regions.
• The universality is independent of whether underlying fluid dynamics is relativistic or nonrelativistic, as relativistic corrections only modify sound (Brillouin) peaks, not the Rayleigh thermal width, leaving the exponent-less fluidity measure unchanged (Abir et al., 2010).
• In high-energy systems such as the QGP, which is produced in relativistic heavy-ion collisions at RHIC/LHC and believed to undergo a liquid–gas–like phase transition with possible critical end point, the fluidity index constraints (e.g., $\mathcal{S}_{\eta\kappa}=1/(6\pi)$) are equally valid. Thus, measurement of η/s via elliptic flow observables at RHIC can be mapped to constraints on κ (thermal conductivity) and the correlation length ξ through the universal fluidity measure.

This universality underpins the robustness of the fluidity index as a comparative metric across fundamental phases of matter, complex fluids, and disordered systems.

4. Theoretical and Experimental Extraction

Extraction of the fluidity index in experiment or simulation typically invokes:

• Rayleigh peak analysis in light or neutron scattering to determine Γ_R and thus $\mathcal{D}_\kappa$;
• Measurement of viscosity via rheometry or hydrodynamic fluctuation analysis;
• Quantification of the correlation length ξ via structure factor maxima or critical opalescence data;
• Direct calculation of the thermal conductivity (κ) and specific heat (C_P).

Once these are measured, the index $\mathcal{S}_{\eta\kappa}$ is computed, with its constancy (1/6π) observed across diverse systems approaching criticality or traversing phase transitions.

In non-equilibrium and soft matter contexts (cell mechanics, glasses, granular flows), alternative but physically related operationalizations arise. For example,

• For biological cells, fluidity as a power-law exponent is extracted from creep compliance (J(t) ∝ t^a), frequency-dependent complex moduli, or phase lag between stress and strain (Maloney et al., 2013).
• In amorphous and granular flows, “fluidity” is parameterized as the local rate of rearrangement or the spatially varying inverse viscosity, often governed by nonlocal continuum equations or order parameter dynamics (Bouzid et al., 2015, Houdoux et al., 2018).

5. Implications for Dynamical and Material Properties

The fluidity index allows quantitative inference of transport constraints and system evolution:

• In QGP, knowledge of η/s along with the universal fluidity measure constrains κ and contextualizes the possible range of other transport coefficients, with direct consequences for the interpretation of heavy-ion collision experiments and lattice QCD calculations (Abir et al., 2010).
• The simultaneous occurrence of low η/s and constrained fluidity index is a fingerprint of nearly “perfect” fluidity—implying minimal momentum dissipation and maximal collective flow.
• For classical and soft materials, knowledge of fluidity indices guides material selection/design for applications where deformation mode (elastic vs. viscous), thermal transport, and response to external stimuli (temperature, crosslinking, etc.) are critical.

Moreover, it highlights the role of underlying processes (thermal diffusion, microstructural rearrangement, defect kinetics) in controlling emergent macroscopic response.

6. Relation to Other Transport Coefficients and Modes

In the broad framework, fluidity indices intertwine shear viscosity, thermal conductivity, entropy, and correlation lengths—unifying diverse transport modalities.

• Momentum transport (viscous relaxation) and energy transport (thermal diffusion) are fundamentally coupled in the fluidity index, as the decay of density fluctuations is governed by both viscous and thermal relaxation rates.
• In mode-coupling analyses, different spectral features (Rayleigh vs. Brillouin peaks) cleanly separate thermal and momentum contributions, enabling distinct but coupled predictions for collective dynamics.
• The universality and exponent-less nature of the advanced fluidity index precludes the appearance of non-universal critical exponents; divergences or strong variations in η or κ as T → T_c cancel in their combination.

ℹ️ Table: Core Fluidity-Index Measures

Measure	Mathematical Form	Interpretation
Shear viscosity	η	Classical dynamical measure
Universal exponent-less	$$\mathcal{S}_{\eta\kappa} = \frac{\eta}{[(\mathcal{D}_\kappa \xi)^{-1} T]}$$	Hydrodynamic + thermal transport, universal
Spectral scaling	$\Gamma^* = \frac{6\pi \eta \Gamma_R}{T q^3}$	Universal scaling near criticality
Power-law exponent (cells)	a from $J(t) \propto t^a$ or $G^*(\omega) = g_0 (i\omega/\omega_0)^a$	Cell mechanics, viscoelastic power-law
η/s	η / s	Heuristic for “perfect” fluidity (non-universal exponents may appear)

7. Broader Theoretical and Experimental Implications

The recognition that fluidity is a deeper, universal property—rather than simply a label for low viscosity—carries implications for:

• Interpreting collective effects in critical phenomena, glassy and amorphous flow, soft matter mechanics, and biological systems;
• Lattice QCD and hydrodynamic modeling, where direct computation or measurement of multiple transport coefficients (not just η) is essential to constrain equations of state or heavy-ion collision dynamics;
• Rational design of experimental programs in soft condensed matter or high-energy physics that use precise, multidimensional coupling of transport measurements (e.g., simultaneous determination of viscosity and thermal conductivity);
• Future theoretical work in unifying hydrodynamic, kinetic, and mode-coupling perspectives for complex, disordered, or strongly correlated systems.

In conclusion, the fluidity-index represents a fundamental, system-spanning measure of the interplay between viscous and thermal transport. Its universal, exponent-less character, precise mathematical formulation, and broad applicability mark it as a pivotal concept in the critical analysis, modeling, and engineering of traditional and nontraditional fluids, spanning domains from QGP to living matter.