AdaNorm: Adaptive Normalization in Deep Learning

• AdaNorm is a family of adaptive normalization and gradient correction techniques that improve deep learning model stability and reduce over-fitting.
• It includes parameter-free LayerNorm variants, domain-adaptive normalization for person re-identification, and optimizer gradient norm correction methods.
• Empirical results demonstrate that AdaNorm enhances generalization and convergence on various benchmarks in NLP, vision, and optimization tasks.

AdaNorm refers to a family of adaptive normalization and gradient correction techniques applied in neural network training, spanning normalization in deep layers without learned affine parameters, adaptive domain-specific batch normalization for domain generalization, and gradient norm correction in optimizers. The approaches share the objective of improving generalization, stability, and efficiency of deep learning methods by adaptively replacing static normalization or update steps with formulations informed by data, historical statistics, or task context.

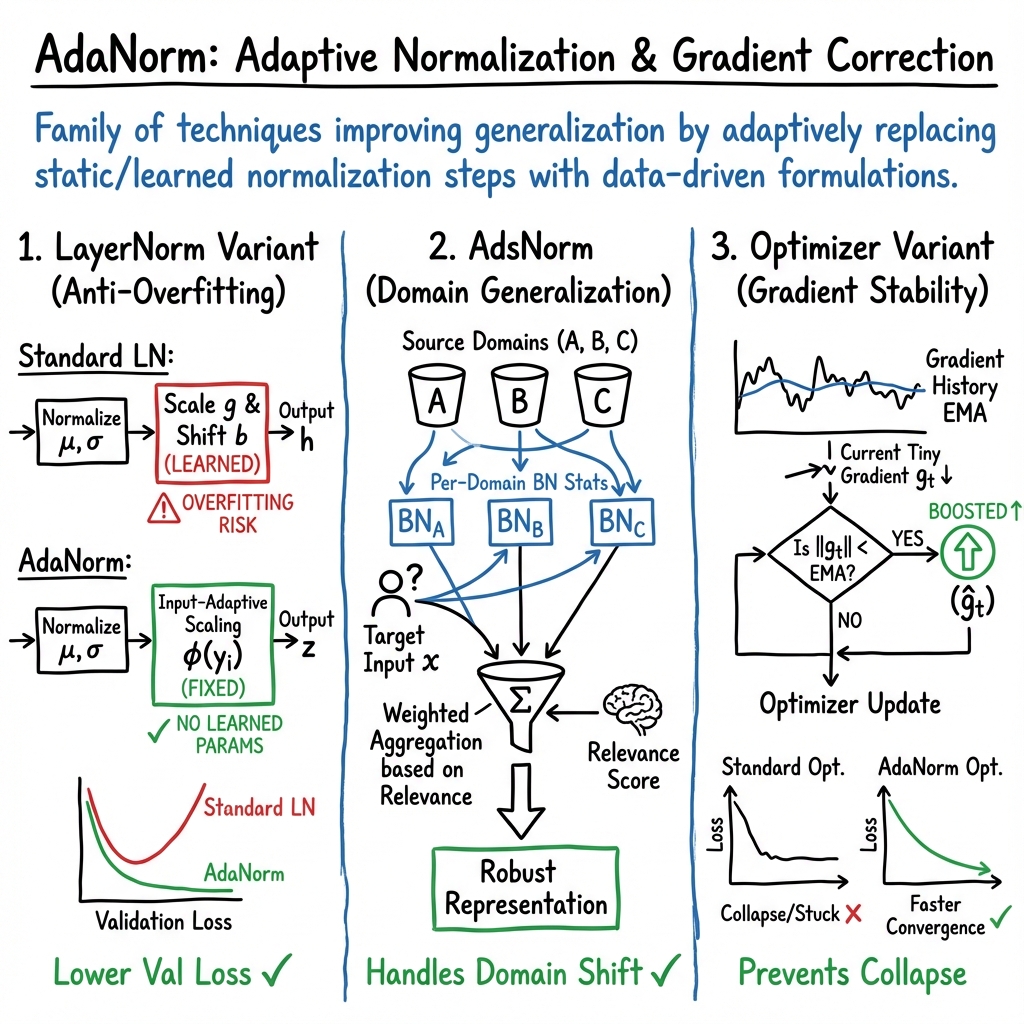
1. Adaptive Normalization in LayerNorm: AdaNorm (Xu et al., 2019)

In the context of layer normalization, AdaNorm is a parameter-free alternative to conventional LayerNorm, created to address the over-fitting induced by the affine parameters (scale/gain and shift/bias). Traditional LayerNorm normalizes input $x \in \mathbb{R}^H$ as

$$\mu = \frac1H\sum_{i=1}^H x_i, \quad \sigma = \sqrt{\frac1H\sum_{i=1}^H (x_i-\mu)^2}, \quad \hat{y}_i = \frac{x_i - \mu}{\sigma}$$

then outputs $h = g \odot \hat{y} + b$ with learned $g, b \in \mathbb{R}^H$. The AdaNorm modification removes $g$ and $b$, substituting a non-learned, input-adaptive scaling: $z_i = \phi(y_i) y_i, \quad \phi(y_i) = C (1-k y_i)$ with hyperparameters $C > 0$, $k = 0.1$. $\phi$ is implemented such that its gradient is detached during back-propagation, preserving the re-centering and re-scaling of backward gradients—a property established as crucial for LayerNorm efficacy.

AdaNorm does not introduce learnable parameters—$C$ and $k$ are static. This design eliminates the propensity for over-fitting caused by learned affine components, as evidenced by lower validation losses compared to vanilla LayerNorm on various NLP and vision benchmarks. Empirical results show AdaNorm improves on seven out of eight tasks including translation (WMT14 En-De BLEU: 28.5 AdaNorm vs. 28.3 LayerNorm) and text classification. A key conclusion from the analysis is that gradient normalization (via inclusion of the $\partial \hat{y}/\partial \mu, \sigma$ Jacobians) is sufficient for generalization; affine parameters can be detrimental.

2. Domain-Adaptive Normalization: AdsNorm for Person Re-ID (Liu et al., 2021)

AdsNorm instantiates an AdaNorm framework for adaptive domain-specific normalization in the person re-identification domain generalization setting, where the target domain is unavailable during training. Each source domain $d$ maintains its own batch normalization statistics $(\mu_d, \sigma^2_d)$: $$\mu_d \leftarrow (1-\alpha)\mu_d + \alpha \frac{1}{N_dHW}\sum_{i,h,w} x^{d}_{i,ch,w}$$

$$\sigma^2_d \leftarrow (1-\alpha)\sigma^2_d + \alpha \frac{1}{N_dHW}\sum_{i,h,w} (x^{d}_{i,ch,w} - \mu_d(c))^2$$

with momentum $\alpha = 0.05$--$0.2$.

AdsNorm uses a shared BN followed by an embedding head $f(\cdot)$ to map each input into a latent space. The domain relevance for a test input $x$ is computed by a softmax over negative squared distances between the embedding $h=f(\mathrm{BN}_\mathrm{shared}(x))$ and each domain prototype: $$w_d(x) = \frac{\exp(-\| h - \mu^h_d \|_2^2/\tau)}{\sum_{d'}\exp(-\| h - \mu^h_{d'}\|_2^2/\tau)}$$ The final aggregated representation is

$z(x) = \sum_{d=1}^D w_d(x) f(\mathrm{BN}_d(x))$

The meta-learning training loop simulates domain shift via hold-one-domain-out: for each mini-batch, one domain acts as meta-train, one as meta-val, encouraging the model to generalize normalization and embedding parameters. The loss combines a relation loss—which enforces intra-class compactness within each domain—and a cross-entropy over the aggregated embedding. Critical implementation features include maintaining per-domain BN buffers without mixing and using simulated adaptation for buffer updates in the meta-train phase without allowing gradients into their states.

AdsNorm demonstrates improved domain generalization, addressing the challenge of domain shift in Re-ID without access to the target domain during training.

3. Adaptive Gradient Norm Correction for Optimizers: AdaNorm (Dubey et al., 2022)

AdaNorm, in the optimizer sense, denotes a gradient normalization strategy applied as a wrapper for SGD-based optimizers including Adam, diffGrad, RAdam, and AdaBelief. The method maintains an exponential moving average (EMA) $e_t$ of the gradient norms: $e_t = \gamma e_{t-1} + (1-\gamma) \|g_t\|_2$ Given the raw gradient $g_t$, if $\|g_t\|_2 < e_t$, the gradient is boosted: $$\hat{g}_t = \frac{c_t}{\|g_t\|_2 + \epsilon} g_t, \quad c_t = \max(e_t, \|g_t\|_2)$$ This correction is applied only to the first moment accumulator of the optimizer; the second moment uses the true $g_t^2$. The approach is generic and implemented by substituting $s_t := \mathrm{normalize}(g_t; e_t)$ for $g_t$ in the update rules. The hyperparameter $\gamma$ (EMA momentum) controls the history scale, with values in $[0.90, 0.99]$ depending on dataset and iteration scale.

Empirical evaluation on CIFAR-10, CIFAR-100, and TinyImageNet with VGG16, ResNet18, and ResNet50 architectures shows that AdaNorm-enhanced optimizers attain higher classification accuracy, especially on TinyImageNet (e.g., AdamNorm-ResNet50 test accuracy 54.44% vs. Adam 48.98%). The key observed effect is that gradient norm remains more stable and representative with AdaNorm, avoiding collapse, which produces better convergence and generalization. Robustness to batch size and learning rate variations is also enhanced.

4. Practical Implementation Guidance

AdaNorm (Layer Normalization Variant)

• Set $k=0.1$ and tune $C \in [0.3,2]$ per task.
• Implement $\phi(y) = C (1 - k y)$ in the forward pass and ensure the gradient is detached (stop_gradient or equivalent).
• No learned parameters—memory and computational footprint is minimal.
• Recommended for Transformer, RNN, and CNN layers especially where over-fitting from LayerNorm’s affine parameters is problematic.
• Use standard pre-norm ordering and Kaiming initialization for stability.

AdsNorm (Domain-Specific BN)

• Maintain unique BN statistics per source domain.
• Combine outputs at inference using soft domain relevance determined by learned latent-space distances.
• During meta-learning, buffer updates are non-gradient and simulated; only backbone and BN scale/shift receive gradients.
• Momentum $\alpha$ typically $0.05$–$0.2$; temperature $\tau \sim 0.1$ for domain relevance weighting.

AdaNorm (Optimizer Variant)

• Apply gradient norm correction to the first-moment only; do not alter the second moment update.
• Default $\gamma=0.95$; set higher for very long runs ($\gamma \to 0.99$).
• Integrates seamlessly into existing SGD-based optimizer implementations; minimal code adjustment required.
• Gains are largest in regimes with unstable or vanishing gradient norms.

5. Comparative Summary Table

Context	Key Mechanism	Parameterization
LayerNorm AdaNorm	Input-adaptive post-norm scaling	Fixed $C,\,k$
AdsNorm	Per-domain BN with relevance weighting	Per-domain BN, meta-learned
Optimizer AdaNorm	EMA-based gradient norm correction	$\gamma$, no new params

These techniques share an adaptive philosophy: normalization or update steps are dynamically tuned based on historical, input, or domain context rather than relying solely on static, hand-tuned, or learned affine transformations. This often reduces over-fitting and improves robustness, especially in settings prone to domain shift or gradient collapse.

6. Critical Insights and Limitations

• In LayerNorm, the normalization’s backward gradient effects—re-centering and re-scaling—are more essential to generalization than forward distribution stabilization or learned parameters.
• Removing learned affine parameters in normalization reduces over-fitting, as evidenced by lower validation loss at similar or improved training loss.
• Per-domain normalization, as in AdsNorm, is effective for domain generalization in vision tasks, where domain shift is significant.
• Boosting low-magnitude gradient updates in optimizers using AdaNorm principles can accelerate convergence and improve final test accuracy, particularly on challenging benchmarks and deeper architectures.
• AdaNorm’s effect may be marginal in already well-conditioned or extremely large networks with stable gradients.
• Linear input-adaptive transforms in AdaNorm are specifically justified by theoretical results; richer nonlinear transforms remain an area for exploration.

7. Connections and Future Directions

The AdaNorm paradigm illustrates a broader trend of replacing learned or hand-crafted normalization with data-driven, adaptivity-enhanced methods. Its instantiations—across normalization, batch statistics, and optimization—point toward improved stability and generalization. Open questions include extending AdaNorm-style normalization to highly over-parameterized regimes (e.g., LLMs), designing nonlinear input-adaptive transforms under strong stability constraints, and leveraging domain-adaptive normalization in online and continual learning settings. The convergence of normalization and adaptive gradient methods offers a fertile ground for structural advances in deep network training.