Active Inference: A Unified Framework

• Active Inference (AIF) is a probabilistic framework that integrates perception, learning, and control through the minimization of variational free energy.
• It formalizes belief updates and action selection by using generative models and natural gradient descent to align predictions with sensory inputs.
• AIF bridges theory and practice by offering a unified mathematical objective that supports both neurobiological modeling and advanced machine learning applications.

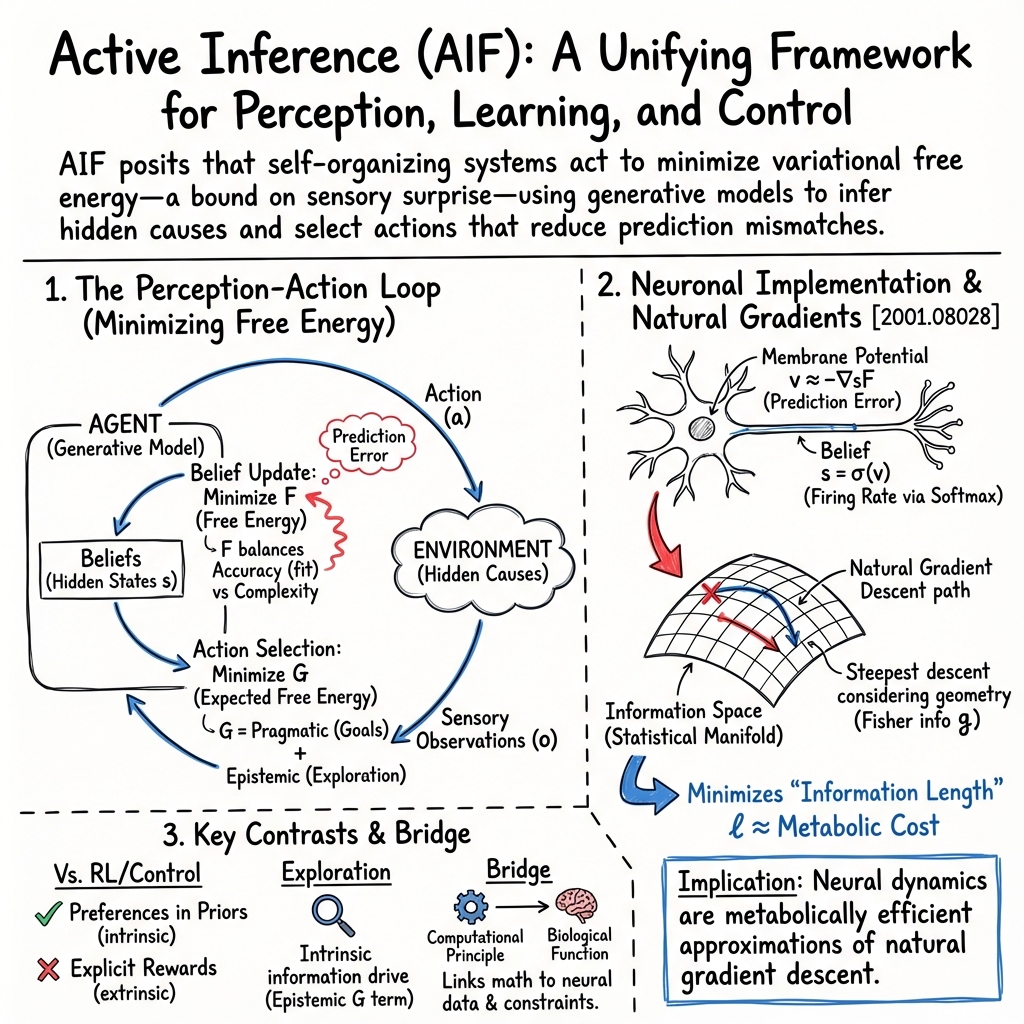
Active Inference (AIF) is a unifying probabilistic framework for perception, learning, and control grounded in the free energy principle, which posits that self-organizing systems act to minimize a variational bound—free energy—on their sensory surprise. Originating in computational neuroscience, AIF formalizes how agents use generative models to infer hidden causes of sensory input and to select actions that reduce the mismatch between predictions and actual outcomes. The resulting theory provides a single mathematical objective that fuses state estimation, planning, information-seeking, and goal-directed behavior.

1. Core Principles and Mathematical Formulation

AIF casts adaptive behavior as a two-fold process: agents construct probabilistic generative models (encoding beliefs about states and observations) and act to minimize variational free energy, F, which quantifies the statistical “distance” between the agent’s beliefs and environmental outcomes. For a distribution Q over hidden states s and observations o (data), free energy is defined as

$$F(Q) = D_{KL}[Q(s) \parallel P(s|o)] - \ln P(o) = \sum_s Q(s) \ln \frac{Q(s)}{P(s|o)}$$

where $D_{KL}$ denotes the Kullback–Leibler divergence between the posterior approximation $Q(s)$ and the model posterior $P(s|o)$. Minimizing F requires balancing accuracy (good predictive fit) with complexity (parsimony of beliefs).

Action arises naturally: the agent selects those interventions on the environment that lead to outcomes best predicted by its generative model, effectively bringing observations in line with model-based expectations. This is formalized by extending variational free energy to “expected free energy” (EFE, denoted G) over future trajectories and candidate policies π:

$$G(\pi) = \mathbb{E}_{Q(o, s | \pi)}[\log Q(s|\pi) - \log P(o, s)]$$

EFE decomposes into an instrumental term (preference for preferred future outcomes) and an epistemic term (expected information gain or exploration drive).

2. Neuronal Dynamics and Biological Plausibility

The AIF framework proposes a physically instantiated process theory in neural systems. State estimation is said to follow a gradient descent on variational free energy, with key aspects encoded as follows (Costa et al., 2020):

• Prediction Error Encoding: The free energy gradient, $\nabla_s F$, represents the mismatch between predicted and actual sensory input, postulated to be directly encoded in mean membrane potentials ($v = -\nabla_s F$) of neuronal populations.
• Belief Update Mechanism: The updated belief over discrete hidden states, $s$, is generated via a softmax transformation applied to these membrane potentials:

$s_{i} = \frac{\exp(v_{i})}{\sum_{j} \exp(v_{j})}$

• Natural Gradient Descent and Metabolic Efficiency: Belief updating in AIF approximates natural gradient descent in information space, guided by the Fisher information metric $g(s)$, ensuring trajectories that are metabolically efficient and minimize “information length” (a Riemannian distance on the simplex), interpreted as minimization of metabolic cost during neural computation.

$$\ell(\gamma) = \int_0^1 \sqrt{\dot\gamma(t)^{\top} g(\gamma(t)) \dot\gamma(t)} \,dt$$

Simulations show that neural dynamics under AIF are nearly as metabolically optimal as exact natural gradient descent paths in belief space—a property that is proposed to have driven evolutionary adaptation of neural architectures (Costa et al., 2020).

3. Implementation Strategies and Practical Algorithms

Implementing AIF in biological or artificial agents involves constructing internal generative models, performing variational inference for belief (posterior) updating, and selecting actions that minimize expected free energy. This proceeds via:

• Belief Update: For discrete latent states,

$s(t+1) = \sigma(\ln s(t) - \epsilon \nabla_s F)$

where $\sigma(\cdot)$ is softmax and $\epsilon$ is a step size.

• Policy Evaluation: Candidate actions or policies are simulated using the generative model, propagating state and observation distributions forward recursively. Expected free energy for each policy is computed, typically as:

$$G(\pi) = KL(Q(s_{\tau}| \pi) \parallel P(s_\tau)) + \mathbb{E}_{Q(s_\tau)}[H(P(o_\tau | s_\tau))]$$

where the first term corresponds to divergence from preferred states (goal-seeking), and the second rewards disambiguation (information gain).

• Action Selection: Policies are assigned probabilities by softmax over $-G(\pi)$, and actions are sampled or selected accordingly.

AIF as instantiated in neural systems is realized via local message-passing (e.g. for synaptic updates or population activity) and is closely aligned with known electrophysiological phenomena, such as mismatch negativity and population-level modulation patterns (Costa et al., 2020).

4. Comparison to Alternative Optimization and Learning Frameworks

Active Inference offers several points of contrast with control-as-inference (CAI), reinforcement learning (RL), and classical optimal control:

• Value Incorporation: Unlike CAI, where reward is represented via explicit optimality variables added to the graphical model, AIF integrates preferences directly into prior distributions on outcomes (i.e., “biased” generative models). This leads to a more unified, enactive model of perception and action (Millidge et al., 2020).
• Exploration–Exploitation Trade-off: The epistemic term in expected free energy operates as an intrinsic information-seeking drive, enabling exploration without explicit exploration bonuses or tuned entropy regularization (Costa et al., 2020).
• Natural Gradient Descent: AIF approximates natural gradient descent on statistical manifolds, using geometry-aware updates that are metabolically and computationally efficient (Costa et al., 2020).

5. Biological, Computational, and Engineering Implications

AIF provides a plausible theory for neural computation and behavioral adaptation:

• Neural Implementation: The correspondence between prediction errors, membrane potentials, and firing rates provides a mechanistic link between AIF theory and observed patterns in cortical and subcortical population dynamics.
• Information-Theoretic Efficiency: The minimization of information length links belief updating to metabolic constraints, with simulations demonstrating nearly optimal use of computational/biological resources (Costa et al., 2020).
• Machine Learning and Control Applications: The close relation between variational message passing in AIF and natural gradients in modern ML suggests avenues for efficient, geometry-aware optimization algorithms, with potential to inform design of artificial agents and controllers in real-world, high-dimensional, or uncertain contexts.

6. Schematic Summary and Key Mathematical Relations

Quantity	Definition/Formula	Interpretation
Variational Free Energy, $F$	$F(Q) = D_{KL}[Q(s)\parallel P(s|o)] - \ln P(o)$	Accuracy–complexity tradeoff for internal model
State Estimation Update	$v = -\nabla_s F$ ; $s = \sigma(v)$ ; $s_{t+1} = \sigma(\ln s(t) - \epsilon \nabla_s F)$	Gradient descent on free energy; softmax maps potential to firing
Natural Gradient Update	$s \leftarrow s - g(s)^{-1} \nabla_s F$	Steepest descent in information (Fisher) space
Information Length, $\ell$	$$\ell(\gamma) = \int_0^1 \sqrt{\dot\gamma^{\top} g(\gamma) \dot\gamma} dt$$	Information-geometry path length (metabolic cost)

Each relation directly encodes either an inference or control policy update, integrating efficient statistical learning with neurobiological constraints.

7. Theoretical and Empirical Consequences

By mapping variational free energy minimization to tangible neural mechanisms and demonstrating equivalence with optimal natural gradient descent for state estimation, AIF is positioned as a computational principle that bridges theory and empirically observed biological function (Costa et al., 2020). This establishes not only a neurobiologically plausible account of adaptive behavior but also a generalizable strategy for constructing both biological and artificial agents capable of efficient perception, learning, and goal-directed control in uncertain environments.