A Mathematical Theory of Payment Channel Networks

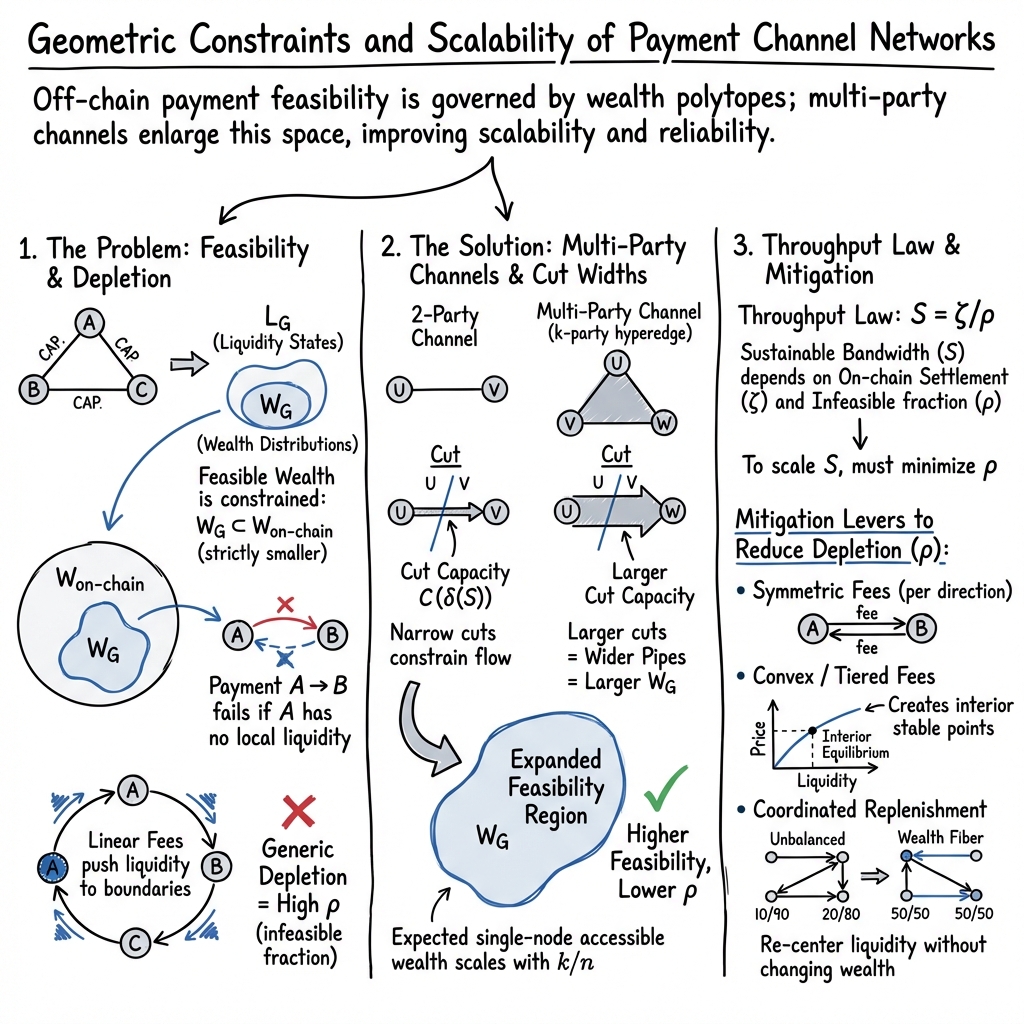
Abstract: We introduce a geometric theory of payment channel networks that centers the polytope $W_G$ of feasible wealth distributions; liquidity states $L_G$ project onto $W_G$ via strict circulations. A payment is feasible iff the post-transfer wealth stays in $W_G$. This yields a simple throughput law: if $ζ$ is on-chain settlement bandwidth and $ρ$ the expected fraction of infeasible payments, the sustainable off-chain bandwidth satisfies $S = ζ/ ρ$. Feasibility admits a cut-interval view: for any node set S, the wealth of S must lie in an interval whose width equals the cut capacity $C(δ(S))$. Using this, we show how multi-party channels (coinpools / channel factories) expand $W_G$. Modeling a k-party channel as a k-uniform hyperedge widens every cut in expectation, so $W_G$ grows monotonically with k; for single nodes the expected accessible wealth scales linearly with $k/n$. We also analyze depletion. Under linear, asymmetric fees, cost-minimizing flow within a wealth fiber pushes cycles to the boundary, generically depleting channels except for a residual spanning forest. Three mitigation levers follow: (i) symmetric fees per direction, (ii) convex/tiered fees (effective flow control but at odds with source routing without liquidity disclosure), and (iii) coordinated replenishment (choose an optimal circulation within a fiber). Together, these results explain why two-party meshes struggle to scale and why multi-party primitives are more capital-efficient, yielding higher expected payment bandwidth. They also show how fee design and coordination keep operation inside the feasible region, improving reliability.

• The paper presents a geometric and combinatorial framework that defines state and wealth polytopes to analyze liquidity feasibility in payment channel networks.
• It quantifies how network topology and channel capacity constraints limit scalability by identifying throughput bottlenecks due to infeasible payment flows.
• The study evaluates mitigation strategies such as symmetric and convex fee schedules, and coordinated rebalancing to address channel depletion and boost capital efficiency.

A Geometric Framework for Payment Channel Network Feasibility and Capital Efficiency

Introduction and Motivation

The paper "A Mathematical Theory of Payment Channel Networks" (2601.04835) presents a comprehensive geometric and combinatorial treatment of payment channel networks (PCNs), with an application focus on the Bitcoin Lightning Network (LN). The author develops a framework for analyzing channel state feasibility, network capital efficiency, channel depletion, and the implications for off-chain scalability. Central to the analysis are two polytopes: the state polytope $L_G$ of feasible channel-level liquidity assignments and the wealth polytope %%%%1%%%% of feasible user-level coin distributions. The interplay between network topology, liquidity constraints, and routing policy is elucidated, revealing intrinsic limitations and levers for enhancing payment reliability and scalability.

Network State and Wealth Polytopes

For a given undirected graph $G(V,E,cap)$ encoding channel connectivity and capacities, the set of feasible liquidity states $L_G$ forms an integer hyperbox of dimension $m=|E|$, reflecting conservation of liquidity per channel. Each feasible state determines a wealth vector $\omega$ through aggregation; the image of $L_G$ under this aggregation is a subset $W_G$ of all possible user wealth assignments.

The volume of $L_G$, given uniform edge capacities, is maximized when all channel capacities are equal:

$|L_G| = \left(\frac{C}{m} + 1 \right)^m$

where $C$ is the total coin supply. The polytope $W_G$ of feasible wealth distributions is strictly smaller than the unconstrained "on-chain" wealth polytope $\mathcal{W}(C,n)$, with a relative volume $r(G) = |W_G|/|\mathcal{W}(C,n)|$ that quantifies loss of flexibility due to liquidity conservation and network sparseness. For networks with $n > 2$, there always exist infeasible wealth vectors $\omega \notin W_G$ that would be realizable on-chain but are unattainable given off-chain channel constraints.

Feasibility of Payments and Throughput Limits

Given a current wealth vector $w \in W_G$, a payment of $a$ from node $i$ to $j$ is feasible if and only if the vector $w' = w - a b_i + a b_j$ remains in $W_G$. The probability $\rho$ that a randomly chosen payment is infeasible serves as a fundamental throughput bottleneck: on-chain operations are required to enable otherwise infeasible off-chain transfers, limiting sustainable LN bandwidth to $\mathcal{S} = \zeta / \rho$, where $\zeta$ is the on-chain settlement rate. For Lightning to support the Visa-scale throughput, the fraction of infeasible off-chain payments must be extremely small ($\rho \ll 1\%$).

The Effect of Channel Topology: Multi-Party Channels and Cut Geometry

A key technical insight is that the feasible region $W_G$ is fundamentally constrained by the network's cut structure. For any subset $S \subset V$, the allowed total wealth $\omega(S)$ is confined to an interval of width equal to the cut capacity $C(\delta(S))$, where $\delta(S)$ comprises all channels crossing the cut. In sparse two-party networks, cut widths are typically narrow, severely limiting $W_G$. Introducing multi-party ($k$-party) channels modeled as hyperedges strictly increases the expected cut width across all cuts, monotonically enlarging $W_G$ as $k$ grows:

$$\mathbb{E}[C(\delta(S))] = m c \cdot q_k(s), \quad q_k(s) = 1 - \frac{\binom{s}{k} + \binom{n-s}{k}}{\binom{n}{k}}$$

For $s=1$ and $k \geq 2$, $q_k(1) = k/n$, showing that the maximum expected wealth a node can control in a $k$-party network grows linearly in $k/n$ for fixed $n, m$. In the degenerate case of a single $n$-party channel, all coins are accessible to all participants, maximizing payment feasibility.

Fiber Structure, Circulations, and Rebalancing

The projection $L_G \to W_G$ partitions $L_G$ into fibers, where each fiber consists of network states yielding the same user-level wealth distribution. The size of a fiber corresponds to the number of strict circulations (cycle-based rebalancings with wealth invariance) available in the current network topology and liquidity configuration. The fiber structure is trivial in trees (liquidity uniquely determined by wealth), but for networks with cycles, the abundance of rebalancing options is governed by the graph's circuit rank.

Channel Depletion and Emergent Structural Imbalances

Under cost-minimizing routing strategies and asymmetric, linear fee schedules, wealth-preserving flows maximize node and network fee potential by pushing cycles toward the boundary of $L_G$, generically leading to channel depletion except for a residual spanning forest. This phenomenon is not a consequence of misconfiguration or irrationality but arises from the interaction of rational economic incentives with the network's geometric constraints. Empirical results confirm that, in maximally fee-efficient states, the number of depleted channels correlates strongly with the circuit rank of the network. Theoretical analysis shows that, in general topologies, high network utilization drives most channels to full depletion, confirming previously observed steady-state phenomena.

Figure 2: The number of depleted channels correlates strongly with the circuit rank of the network, indicating that cycles tend toward depletion under rational, fee-maximizing strategies.

Mitigation Strategies for Depletion

Three main mitigation levers are analyzed:

• Symmetric Fees: Enforcing equal fees in both directions eliminates the net economic pressure toward depletion along cycles. This approach, while technically straightforward, is unlikely to gain operator support due to negotiation frictions.
• Convex/Tiered Fees: Adopting convex, utilization-responsive fee schedules introduces interior equilibrium points that stabilize liquidity and prevent boundary depletion. Simulation demonstrates that convex fees promote balanced usage and maintain median liquidity, but deployment challenges arise due to lack of real-time path cost visibility by senders.
• Coordinated Replenishment: Collaborative selection of an optimal circulation within each fiber (e.g., via integer quadratic optimization near a desired central state) can rebalance liquidity non-custodially, but this requires significant coordination, full state disclosure, and often centralized orchestration.

Scalability Implications and Theoretical Limits

The geometry developed in the paper rigorously establishes that purely two-party LN topologies have a structurally limited feasible region $W_G$, yielding a non-negligible steady-state rate $\rho$ of infeasible payments even under optimal routing and perfect information. Thus, without the adoption of multi-party channels (factories, coin-pools) to enlarge cut widths and $W_G$, off-chain throughput remains fundamentally constrained by the interplay of $\zeta$ and $\rho$. Allowing trusted credit would trivially solve the feasibility constraint, but this is incompatible with the non-custodial, trust-minimized design goals.

Future Directions and Protocol Evolution

The theoretical machinery identifies clear avenues for protocol improvement:

• Expand $W_G$ and reduce $\rho$ with multi-party primitives and optimized capital placement.
• Amortize on-chain bandwidth via batching and enhance $\zeta$ with innovative channel factory mechanics.
• Adopt fee schedules and protocol support to mitigate depletion and maintain interior liquidity states.

The results motivate the measurement of $\rho$ and depletion in live networks and highlight the necessity of aligning incentive structures and routing protocols with intrinsic geometric constraints, rather than focusing solely on ad-hoc adjustments. The feasibility envelope defined by $W_G$—and its enlargement by advanced primitives—emerges as a central design objective in the evolution of off-chain scalability.

Conclusion

This paper provides an authoritative account of the mathematical underpinnings that determine the operational limits, reliability, and capital efficiency of payment channel networks. By geometrically characterizing feasible liquidity and wealth polytopes, and relating these to network topology and incentive-driven routing, it precisely delineates both hard structural boundaries and actionable levers for improvement. Two strong assertions are substantiated: (1) two-party channel networks are inherently unscalable for high-throughput, trust-minimized payment systems, and (2) depletion is a direct consequence of rational, fee-minimizing flow under standard protocols. The theoretical framework offers valuable guidance for the design and deployment of future payment protocols and clarifies the necessity of multi-party primitives, sophisticated fee structures, and coordination mechanisms to achieve practical and reliable off-chain scalability.