Forecasting the U.S. Treasury Yield Curve: A Distributionally Robust Machine Learning Approach

Abstract: We study U.S. Treasury yield curve forecasting under distributional uncertainty and recast forecasting as an operations research and managerial decision problem. Rather than minimizing average forecast error, the forecaster selects a decision rule that minimizes worst case expected loss over an ambiguity set of forecast error distributions. To this end, we propose a distributionally robust ensemble forecasting framework that integrates parametric factor models with high dimensional nonparametric machine learning models through adaptive forecast combinations. The framework consists of three machine learning components. First, a rolling window Factor Augmented Dynamic Nelson Siegel model captures level, slope, and curvature dynamics using principal components extracted from economic indicators. Second, Random Forest models capture nonlinear interactions among macro financial drivers and lagged Treasury yields. Third, distributionally robust forecast combination schemes aggregate heterogeneous forecasts under moment uncertainty, penalizing downside tail risk via expected shortfall and stabilizing second moment estimation through ridge regularized covariance matrices. The severity of the worst case criterion is adjustable, allowing the forecaster to regulate the trade off between robustness and statistical efficiency. Using monthly data, we evaluate out of sample forecasts across maturities and horizons from one to twelve months ahead. Adaptive combinations deliver superior performance at short horizons, while Random Forest forecasts dominate at longer horizons. Extensions to global sovereign bond yields confirm the stability and generalizability of the proposed framework.

• The paper introduces a distributionally robust forecast framework that minimizes worst-case expected loss for U.S. Treasury yield predictions.
• It integrates high-dimensional Random Forests with FADNS models using adaptive forecast combination techniques to capture yield dynamics across horizons.
• Robust aggregation methods consistently reduce RMSFE and stabilize forecast errors, particularly during market stress and regime shifts.

Distributionally Robust Machine Learning for U.S. Treasury Yield Curve Forecasting

Introduction

The forecasting of the U.S. Treasury yield curve remains a foundational challenge in financial econometrics and operations research. Yield curves both reflect and drive policy, macroeconomic expectations, and market stress, with U.S. Treasuries serving as the global standard for interest-rate benchmarks. The paper "Forecasting the U.S. Treasury Yield Curve: A Distributionally Robust Machine Learning Approach" (2601.04608) reconceptualizes forecasting under distributional uncertainty as a min–max decision problem, placing explicit emphasis on the minimization of worst-case expected loss over admissible forecast-error distributions. The study introduces a distributionally robust ensemble framework that unifies parametric and nonparametric ML models through adaptive forecast combination and robust optimization. This essay presents a technical summary, quantifies empirical results, and situates the work within the context of current and future research directions in robust financial ML.

Methodological Framework

The framework integrates three primary components:

1. FADNS Parametric Models: Rolling-window Factor-Augmented Dynamic Nelson–Siegel (FADNS) models utilize principal components from macroeconomic indicators to capture latent yield curve dynamics (level, slope, curvature) and state evolution via VAR(1) processes. Empirical alignment with economic regimes is validated through structural break detection (PELT, CUSUM).
2. High-Dimensional Random Forests: RF architecture models nonlinear mappings from lagged yields and extensive economic indicator panels (p=111) to future yields. Trees are grown via conventional CART procedures and regularized by randomized hyperparameter search and cross-validation, respecting real-time data availability via appropriate lagging and normalization.
3. Distributionally Robust Forecast Combination: Adaptive forecast aggregation is implemented via a suite of classical and robust weighting mechanisms (e.g., equal weights, rank, stacking, minimum-variance, LAD). The robust weighting schemes leverage expected shortfall penalization and ridge-regularized covariance matrices to stabilize weights against moment uncertainty and downside tail risk.

This ensemble methodology operates in a rolling window setting, with forecast evaluation across 15 Treasury maturities and horizons ranging from 1 to 12 months.

Empirical Results and Quantitative Evaluation

Random Forest Performance

Across 10 independent runs, the RF model displays high predictive stability: the RMSFE is largely invariant to forecast horizon length, with short-end maturities presenting higher error (24–25 bps) and long-end maturities achieving lowest RMSFE (≈13 bps). Deviations across seeds are minimal, underscoring the reliability of the RF approach under cross-validation and rolling-window regimes.

FADNS Model Outcomes

The DNS model's RMSFE deteriorates sharply with increasing forecast horizon, reflecting error accumulation in recursive low-dimensional systems (e.g., >130 bps by 12 months for most maturities). FADNS augmentation improves short-horizon error metrics, with RMSFE reductions of 5–15 bps at lower maturities, but fails to halt long-horizon error propagation. Beyond 6 months, RMSFE rapidly exceeds 120–150 bps.

Robust Forecast Combination

When combining RF and FADNS forecasts, robust aggregation rules—LAD, DRO-ES, DRMV—consistently produce lower RMSFE, especially at short horizons and high cross-model heterogeneity. Rank-based and tail-risk penalizing schemes outperform naive averaging and OLS-style weighting. The performance advantage is amplified during regime shifts and episodes of market stress.

Time-Series and Weight Dynamics

During the COVID-19 crisis and post-2022 tightening cycle, robust combinations yield smoother, less volatile forecast errors (Figure 1), while weight allocations shift sharply between RF and FADNS pools depending on in-sample tail risk and covariance structure (Figures 4–6). Rapid dynamic reallocation enhances responsiveness to structural breaks.

Figure 1: One-month-ahead forecast error dynamics of hybrid RF–FADNS forecast combinations across U.S. Treasury maturities.

Figure 2: Weight dynamics under distributionally robust mean–variance (DRMV) forecast combination.

Figure 3: Weight dynamics under distributionally robust expected shortfall (DRO–ES) forecast combination.

Figure 4: Weight dynamics under hybrid distributionally robust (DRO–MIX) forecast combination.

Predictive Stability and Robustness

The framework generalizes to joint-maturity and cross-country contexts. In multi-output RF models for U.S. Treasuries (2010–2025), RMSFE remains stable across seeds and horizons. Inclusion of Treasury International Capital (TIC) variables yields marginal RMSFE improvement at the long end, with principal impact at 30-year, 12-month horizon (Figure 5).

Figure 5: Comparing U.S. benchmark Treasury yield forecasts with additional Treasury supply variables (TIC).

Feature Attribution and SHAP Analysis

Global SHAP values demonstrate high stability of RF feature importance rankings across random seeds and maturities (Figure 6). Short-horizon forecasts emphasize high-frequency real activity indicators, while longer horizons are dominated by price, income, and financial conditions metrics. Inflation, labor, and financial variables remain persistently influential.

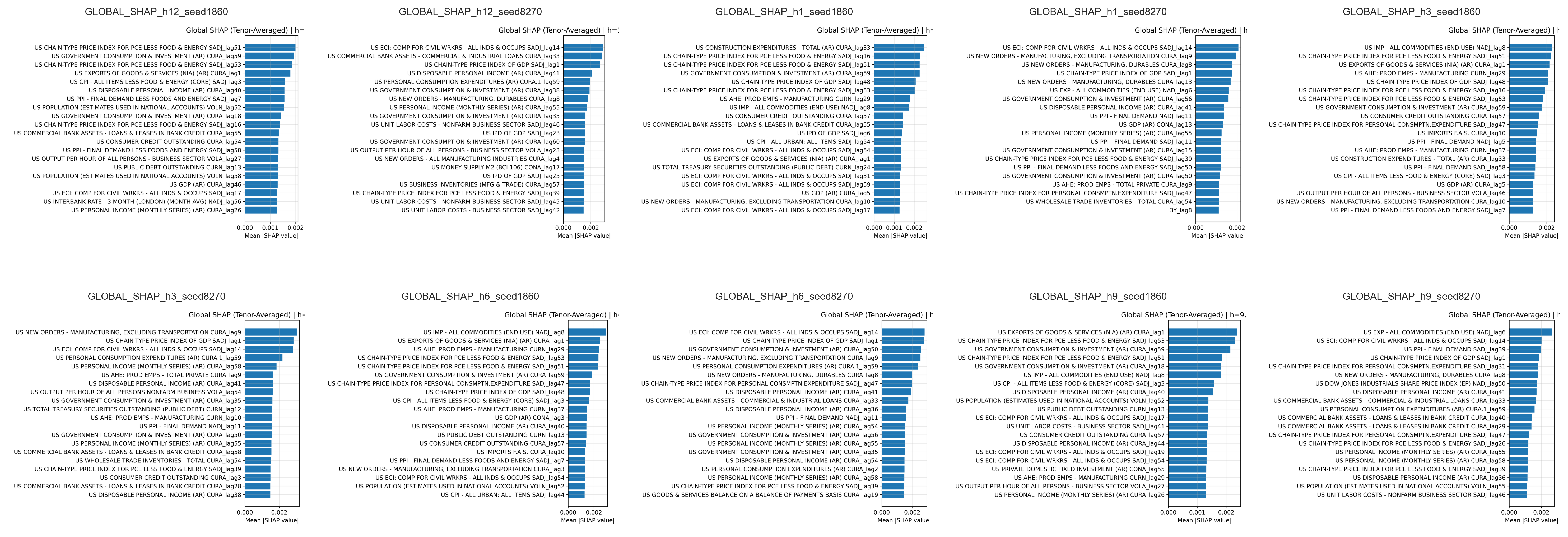
Figure 6: Maturity-averaged global SHAP values for the Random Forest model across forecast horizons.

International Generalizability

The RF architecture is robust across global sovereign bond markets, maintaining RMSFE (15–45 bps) for 10-year benchmarks in Canada, China, Germany, Japan, Malaysia, UK, and US, modulated by local yield volatility.

Theoretical and Practical Implications

The explicit recasting of yield curve forecasting as a minimax problem under moment uncertainty provides a theoretically principled pathway to robust ML deployment in financial contexts. Distributionally robust optimization (DRO) disciplines flexible ensemble learners by penalizing downside risk and stabilizing covariance estimation, particularly in the presence of heavy-tailed errors and structural breaks—a feature acute in high-frequency financial data and policy-driven environments.

The implementation of adaptive, tail-aware forecast combination is critical when aggregating structurally heterogeneous models. Robust weighting not only enhances predictive accuracy but fundamentally mitigates risk of portfolio misallocation and business decision regret under policy shocks and unknown error distributions.

Sophisticated interpretability diagnostics via SHAP yield robust, actionable attribution metrics, though causal inference remains unaddressed.

Future Research Trajectories

Further work is warranted to:

• Develop real-time forecasting with explicit modeling of indicator publication lags and nowcasting for incomplete data panels.
• Extend SHAP and related interpretability tools to dynamic, time-dependent attribution and decision feedback.
• Construct bootstrapped, distributionally robust confidence intervals for forecasted yield curves.
• Explore generalization to advanced ML architectures (e.g., deep learning, transformers) under DRO regularization to control model instability under non-stationary distributions.
• Tailor robust ensemble frameworks for other asset classes (credit, foreign exchange, equities) and joint forecasting/portfolio allocation under ambiguity.

Conclusion

This study establishes a unified, distributionally robust ML framework for U.S. Treasury yield curve forecasting, integrating high-dimensional Random Forests and factor-augmented term structure models via adaptive, tail-risk-aware combination. Quantitatively, robust aggregation delivers marked RMSFE improvements and error stabilization, particularly under market stress and forecasting horizon extension. Pragmatically, the paradigm shifts forecasting and financial decision support toward robust, stable optimization under deep uncertainty. These methodological foundations and empirical results motivate broader exploration of robust ML for critical decision support in the face of evolving financial environments.