Topological Spatial Graph Coarsening (2512.24327v1)

Abstract: Spatial graphs are particular graphs for which the nodes are localized in space (e.g., public transport network, molecules, branching biological structures). In this work, we consider the problem of spatial graph reduction, that aims to find a smaller spatial graph (i.e., with less nodes) with the same overall structure as the initial one. In this context, performing the graph reduction while preserving the main topological features of the initial graph is particularly relevant, due to the additional spatial information. Thus, we propose a topological spatial graph coarsening approach based on a new framework that finds a trade-off between the graph reduction and the preservation of the topological characteristics. The coarsening is realized by collapsing short edges. In order to capture the topological information required to calibrate the reduction level, we adapt the construction of classical topological descriptors made for point clouds (the so-called persistent diagrams) to spatial graphs. This construction relies on the introduction of a new filtration called triangle-aware graph filtration. Our coarsening approach is parameter-free and we prove that it is equivariant under rotations, translations and scaling of the initial spatial graph. We evaluate the performances of our method on synthetic and real spatial graphs, and show that it significantly reduces the graph sizes while preserving the relevant topological information.

• The paper introduces a parameter-free, triangle-aware spatial graph coarsening method that preserves key topological invariants using persistent diagrams.
• It employs a novel filtration approach that optimally balances graph sparsity and topological fidelity while remaining robust under similarity transformations.
• Empirical evaluations on synthetic annuli, urban road networks, and fungal mycelia confirm effective reduction with minimal loss of crucial structural features.

Topological Spatial Graph Coarsening: A Technical Synthesis

Overview and Motivation

The paper "Topological Spatial Graph Coarsening" (2512.24327) introduces a rigorously-defined, parameter-free procedure for reducing the complexity of spatial graphs while preserving their principal topological features. Spatial graphs, representing systems such as transport networks, biological branching structures, and molecules, pose unique challenges for reduction because both geometric and topological properties are integral to their semantics. Traditional graph sparsification and coarsening methods provide limited topological guarantees, while existing TDA techniques have not been tailored to the spatial-graph regime or have imposed unsuitable simplifications.

The authors propose a new coarsening framework that collapses short edges based on a novel triangle-aware filtration, thereby retaining essential topological invariants as measured by persistent diagrams. The approach seeks an optimal trade-off between sparsity and topological faithfulness, with invariance properties under similarity transformations. The method is evaluated on both synthetic and real-world data, including urban road networks and biological fungal structures, and is supported by formal theoretical analysis.

Technical Foundations

Spatial Graph Coarsening Procedure

A spatial graph $G=(V,E,X)$ consists of nodes $V$ with positions $X$ in Euclidean space and edges $E$ with associated Euclidean lengths. Coarsening is governed by a spatial threshold parameter $\theta$: all edges shorter than $\theta$ are collapsed, with their associated nodes grouped into "hypernodes." The process is defined so that each hypernode's spatial position is derived either by averaging merged node positions (useful for geometrically-representative skeletons) or assigning it the coordinates of the highest-degree constituent node (appropriate for infrastructural networks).

Graph reduction for increasing $\theta$ yields a hierarchy of coarsened graphs, ranging from the original graph (for small $\theta$) to a single-vertex trivial graph (for very large $\theta$).

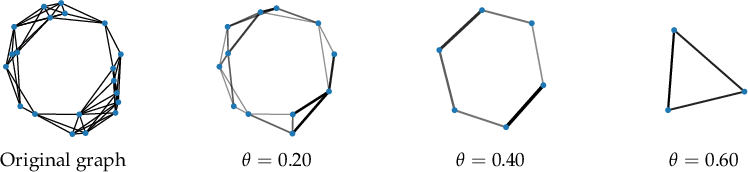
Figure 1: Examples of pruned graphs as the coarsening parameter $\theta$ increases, displaying progressive edge/node collapses.

Topological Data Analysis for Spatial Graphs

Central to this approach is the use of persistence diagrams to quantify and track topological features across a filtration of graphs. Classic persistent homology is adapted to spatial graphs by defining a VR-like filtration where the pairwise metric is the shortest path over the graph, as opposed to standard Euclidean or graph-theoretical distance.

However, direct application of this filtration can result in the immediate disappearance of cycles formed by triangles ("empty triangles"). To address this, the authors introduce the triangle-aware graph filtration, wherein two-simplices (triangles) are included in the filtration at scales determined by the minimal sum of relevant shortest-path distances, rather than being dictated solely by the largest constituent edge. This adaption ensures cycles induced by triangles are represented in the persistence diagram with persistence reflecting their geometric properties.

Figure 2: Example of a spatial graph and its associated persistence diagram, distinguishing 0-dimensional (components) and 1-dimensional (cycles) features.

Figure 3: Comparative diagrams for an original and coarsened spatial graph, along with their respective persistence diagrams, showing retention of primary topological features and removal of topological noise.

Optimization and Invariance Properties

The critical contribution lies in selecting the coarsening parameter $\theta$ that achieves optimal trade-off between graph simplification and preservation of salient topological features. This is formulated as minimizing a score

$$S_\theta(G) = \frac{|f^E_\theta(G)|}{|E|} + \lambda \cdot d_B(PD(G), PD(f_\theta(G)))$$

where $d_B$ is the bottleneck distance between the persistence diagrams of the original and coarsened graphs, and $\lambda$ normalizes the contributions.

Theoretically, the procedure is shown to be equivariant under similarity group actions (rotation, translation, scaling): coarsening commutes with such transformations up to appropriately scaled parameter values. This ensures the method's robustness for spatial data independent of global positioning or scale.

Figure 4: The spatial graph coarsening procedure produces outputs equivariant under rotation, translation, and scaling transformations (element of $Sim(p)$).

Empirical Demonstration

The authors provide thorough empirical validation on both synthetic and real datasets.

• Synthetic Annulus: Random points on an annulus are used to construct a spatial graph. The method robustly discovers a reduction threshold at which primary cycles (corresponding to the annulus structure) are retained while collapsing topological noise.

Figure 5: A synthetic annulus spatial graph before and after optimal coarsening, showing the preservation of topological cycles.

• Road Network (Marseille): Application to an urban road network demonstrates the method's utility for large sparse graphs with infrastructural semantics. Degree-positioning is used to anchor supernodes to important intersections.

Figure 6: Road network of Marseille, France: complexity is strongly reduced via the coarsening procedure, retaining major routes and intersections.

• Fungal Mycelia: On a curated dataset of fungal networks, the method is further validated by integrating biophysically motivated edge weights (resistances) for coarsening. Classifiers trained on reduced graphs maintain comparable accuracy to those on original graphs for predicting environmental conditions (such as presence/absence/type of grazers), thus empirically demonstrating strong information retention under substantial graph simplification.

Figure 7: Experimental images and extracted spatial graphs for fungal mycelia grown with and without grazers.

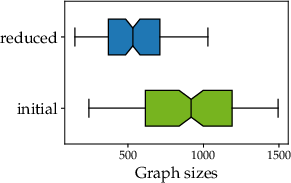
Figure 8: Distribution of optimal reduction levels ($\alpha^*$) over the fungal dataset, indicating variable dataset-specific reduction degrees.

Figure 9: Coarsening on a fungus graph in the absence of grazers.

Figure 10: Coarsening on a fungus graph with small grazers.

Figure 11: Coarsening on a fungus graph with large grazers.

The classification task reveals only minor degradation in predictive accuracy despite the substantial reduction in graph size, indicating that the main topological drivers for classification are preserved.

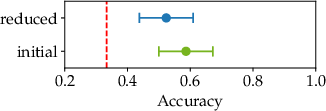
Figure 12: Random forest classification accuracy before and after coarsening, with overlapping confidence intervals and only marginal decrease.

Implications and Future Directions

This work formalizes a topologically informed, parameter-free coarsening pipeline for spatial graphs that is both theoretically sound and computationally realizable. Its symmetry-equivariant nature and explicit use of adapted TDA tools fill a critical gap for scientific and engineering domains relying on geometric graphs.

The main theoretical implication is the demonstration that meaningful topology-driven reduction can be achieved with strong formal guarantees and without user-specified parameters. Empirical findings suggest that topologically salient features suffice for a wide range of applied tasks, implying the possibility of safely compressing large spatial networks for downstream machine learning and data analysis.

In practical settings, this approach opens avenues for efficient storage, visualization, and learning over large-scale spatial networks, from biological to infrastructural systems. Prospective extensions include:

• Refinement of grid search strategies for $\theta$ via smarter discretizations;
• Extension to shape or elastic graphs with richer edge geometry;
• Exploration of inverse procedures to determine which local graph structures correspond to persistent topological features in a target persistence diagram.

Conclusion

The "Topological Spatial Graph Coarsening" framework provides a mathematically principled, comprehensive solution for reducing the complexity of spatial graphs while rigorously preserving their key topological characteristics. By integrating adapted persistent homology with a provably equivariant reduction algorithm, the method offers robust and application-agnostic simplification, extensible to diverse domains and tasks. Future work promises deeper connections between TDA, geometric representation learning, and applied network analysis.