Computing parameters that generalize interval graphs using restricted modular partitions (2512.22975v1)

Abstract: Recently, Lafond and Luo [MFCS 2023] defined the $\mathcal{G}$-modular cardinality of a graph $G$ as the minimum size of a partition of $V(G)$ into modules that belong to a graph class $\mathcal{G}$. We analyze the complexity of calculating parameters that generalize interval graphs when parameterized by the $\mathcal{G}$-modular cardinality, where $\mathcal{G}$ corresponds either to the class of interval graphs or to the union of complete graphs. Namely, we analyze the complexity of computing the thinness and the simultaneous interval number of a graph. We present a linear kernel for the Thinness problem parameterized by the interval-modular cardinality and an FPT algorithm for Simultaneous Interval Number when parameterized by the cluster-modular cardinality plus the solution size. The interval-modular cardinality of a graph is not greater than the cluster-modular cardinality, which in turn generalizes the neighborhood diversity and the twin-cover number. Thus, our results imply a linear kernel for Thinness when parameterized by the neighborhood diversity of the input graph, FPT algorithms for Thinness when parameterized by the twin-cover number and vertex cover number, and FPT algorithms for Simultaneous Interval Number when parameterized by the neighborhood diversity plus the solution size, twin-cover number, and vertex cover number. To the best of our knowledge, prior to our work no parameterized algorithms (FPT or XP) for computing the thinness or the simultaneous interval number were known. On the negative side, we observe that Thinness and Simultaneous Interval Number parameterized by treewidth, pathwidth, bandwidth, (linear) mim-width, clique-width, modular-width, or even the thinness or simultaneous interval number themselves, admit no polynomial kernels assuming NP $\not\subseteq$ coNP/poly.

• The paper presents linear-time kernelization for the thinness parameter via interval-modular partitioning, efficiently reducing each module without altering graph properties.
• It devises an FPT approach for the simultaneous interval number by restricting cluster modules and applying bounded branching over interval assignments.
• The study establishes both positive algorithmic techniques and negative kernelization results with classical width parameters, guiding future research in graph decompositions.

Computing Interval-Related Graph Parameters via Modular Partitioning: Algorithmic and Structural Insights

Introduction

This paper investigates the computation of two parameters that quantify proximity to interval graphs—the thinness and the simultaneous interval number—by leveraging modular partitioning strategies that restrict modules to belong to tractable classes (interval or cluster graphs). The study builds on the recent notion of $\mathcal{G}$-modular cardinality introduced by Lafond and Luo, which captures the minimal number of modules required to partition a graph such that each module induces a graph in $\mathcal{G}$. The analysis centers on optimizing fixed parameter tractability (FPT) and kernelization for Thinness and Simultaneous Interval Number when parametrized by these modular cardinalities, particularly with $\mathcal{G}$ being the interval or cluster class.

Background and Parameterizations

Thinness generalizes interval graphs by considering ordered vertex partitions that control the spread of adjacencies, formally capturing the minimal partition size allowing certain propagation properties in linear vertex orders. The Simultaneous Interval Number generalizes interval representation further by allowing multiple interval assignments with label sets, requiring adjacency if intervals and labels intersect. Both parameters are known to be NP-hard to compute on general graphs, with no known FPT or XP algorithms parameterized by solution size or other classical parameters.

The paper emphasizes parameterizations based on modular partitions into interval or cluster modules, which generalize parameters such as neighborhood diversity and twin-cover. A key focus is the interval-modular cardinality, denoted $(G)$, and cluster-modular cardinality, denoted $(G)$, with $(G) \leq (G)$. Parameterization with respect to these, or to solution size, treewidth, pathwidth, and clique-width, is systematically studied, including negative results for compact kernelizations in several cases.

Algorithmic Results: Linear Kernels and FPT

The authors contribute two main algorithmic advances:

1. Linear Kernels for Thinness Parameterized by Interval-Modular Cardinality:

A linear-time kernelization is achieved by reducing each module (from an optimal interval-modular partition) to at most two vertices (if it is not a clique) or a single vertex (if it is a clique), without affecting the thinness of the overall graph. This reduction exploits specific contractibility properties:

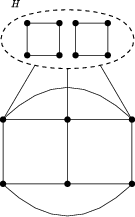
Figure 2: $\mathrm{thin}(G) = 3$; exemplifies thinness in a modular partition context.

Under this reduction, the resulting kernel size is at most twice the interval-modular cardinality of $G$. The result directly transfers to fixed-parameter tractability and kernelization for Thinness parameterized by neighborhood diversity, twin-cover, and vertex cover due to their relation to cluster-modular cardinality, with explicit polynomial, in fact linear, upper bounds.

2. FPT for Simultaneous Interval Number with Cluster-Modular Cardinality and Solution Size:

The Simultaneous Interval Number problem is shown to be FPT when parameterized by the sum of cluster-modular cardinality and the target solution value $d$ (size of simultaneous interval representation). The strategy involves: - Reducing each cluster module to at most $d$ representative vertices (if their label sets must be pairwise disjoint), - Enumerating over a bounded number of interval/labeling assignments, - Solving a constrained labeling/interval assignment task via explicit bounded branching.

This paradigm yields FPT algorithms for parameterization by twin-cover and neighborhood diversity (plus solution size), via their connections to cluster-modular cardinality.

Structural Insights and Negative Results

The study furnishes several combinatorial and algorithmic lemmas, formalizing how module reduction preserves thinness or simultaneous interval number. Specifically, the contraction of a complete or interval module (appropriately reduced to few vertices) does not increase thinness; otherwise, careful counterexamples demonstrate the limits of this approach, especially with thinness-2 modules.

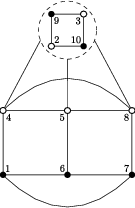
Figure 4: A consistent solution with two classes for a specific $G'$, illustrating subtle discrepancies in thinness under certain module replacements.

Figure 6: Vertex labeling for $G' \setminus H'$ showing name assignments in a key counterexample used to prove the impossibility of some module reductions preserving thinness.

An important negative result is established: Thinness and Simultaneous Interval Number do not admit polynomial kernels parameterized by treewidth, pathwidth, bandwidth, linear mim-width, clique-width, modular-width, nor by the thinness or simultaneous interval number themselves, unless $\mathsf{NP} \subseteq \mathsf{coNP}/\mathsf{poly}$. The methods used involve standard kernelization lower bound machinery via OR-compositions and cross-compositions.

Implications and Future Directions

The results have substantial algorithmic implications: several NP-hard interval graph parameterizations become FPT and allow efficient preprocessing under structural restrictions—most notably interval-modular and cluster-modular partitions. The developed algorithms and kernels also lay groundwork for tractable approaches to thinness in real-world graphs, where such structural decompositions can be feasibly computed.

The paper leaves several open problems, particularly the parameterized complexity of Thinness and Simultaneous Interval Number with solution size as the parameter, and the existence of polynomial kernels for Thinness parameterized by twin-cover or vertex cover.

On a theoretical level, this line of research clarifies the hierarchy of graph decompositions, linking neighborhood diversity, twin-cover, modular-width, and module-based partitions, and delineating which width parameters admit effective preprocessing for interval-based measures.

Conclusion

This paper advances the theory and computation of interval-graph related parameters, providing linear-time kernelization for Thinness parameterized by interval-modular cardinality, and FPT algorithms for Simultaneous Interval Number using cluster-modular cardinality plus solution size. Through sharp contraction results and careful combinatorial analysis, it establishes both positive and negative results on the tractability and kernelizability of these parameters under a range of width measures. The work elucidates the complexity landscape of these parameters and suggests new directions for fixed-parameter algorithms on structured graph classes, with practical and foundational consequences for algorithmic graph theory.