Experimental estimation of Asymmetry of Radiation for Wheeler-Feynman theory for gravitational waves (2512.20692v1)
Abstract: Wheeler-Feynman absorber theory assumes there should be both retarded EM waves but also advanced, however, with symmetric 1/2-1/2 contributions. In contrast, observed Asymmetry of Radiation like inspiraling has lead to currently default assumption of 1-0 only retarded. Any convex combination is allowed, its choice should depend on the boundary conditions like imbalance between absorbers and emitters - while we have domination of absorbers, it does not need to be complete, suggesting to estimate emitters/absorbers asymmetry parameter from data. It could lead to confirmation of current assumption, or requirement to also include advanced waves into considerations. Experimental estimation of such Asymmetry of Radiation is currently difficult for EM waves due to asymmetry between receivers and transmitters. However, e.g. LIGO just measures lengths, which are invariant to T/CPT symmetry, making available gravitational wave observations appropriate for such estimation. We also discuss other arguments for nonzero contributions of advanced waves. For example gravitational observation of e.g. neutron star merger, with required but clearly missing (retarded) EM counterpart, would leave possibility of being advanced wave. Also there are observed events happening too early according to current knowledge e.g. mergers of black holes in the Mass Gap, or insufficient number of retarded sources e.g. for vibrations of the Universe observed by Pulsar Timing Arrays.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper looks at a big idea in physics: whether waves can go both “forward in time” and “backward in time,” and how much each kind happens in the real universe. The author focuses on gravitational waves (the tiny ripples in spacetime produced when huge objects like black holes move) and suggests a way to test, using data from LIGO and similar observatories, how asymmetric the radiation is—meaning how much it prefers the forward direction over the backward one.
Key questions the paper asks
- Are we right to assume that only “forward-in-time” waves (called retarded waves) exist in practice?
- Could there be a small amount of “backward-in-time” waves (called advanced waves) in the real world?
- If yes, can we measure how much advanced wave contribution there is using gravitational wave data?
- What would that tell us about the universe and the direction of time?
How the paper approaches the problem
Think of dropping a stone in a pond: the equations that describe the ripples don’t care if you play the video forwards or backwards—the math works either way. Physics is similar: its fundamental equations are mostly time-symmetric (they don’t change if you flip time). But the actual world looks time-asymmetric—we see cups break, not un-break; stars spiral in and merge, not spiral out and separate.
- Retarded waves: These are the usual waves—causes happen, then effects later (like turning on a light and then seeing light reach you).
- Advanced waves: In the math, you can also have waves that look like they come from the future and reach you “before” the source acts when you play the movie backwards. They’re allowed by the equations but are not part of the standard assumption about how nature behaves.
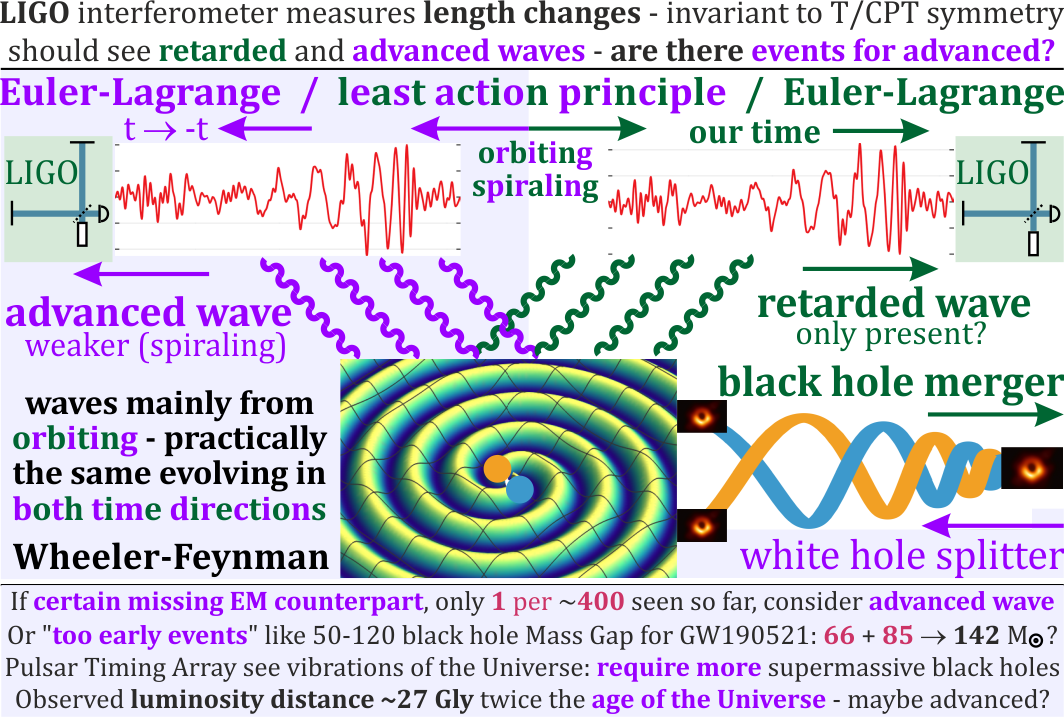
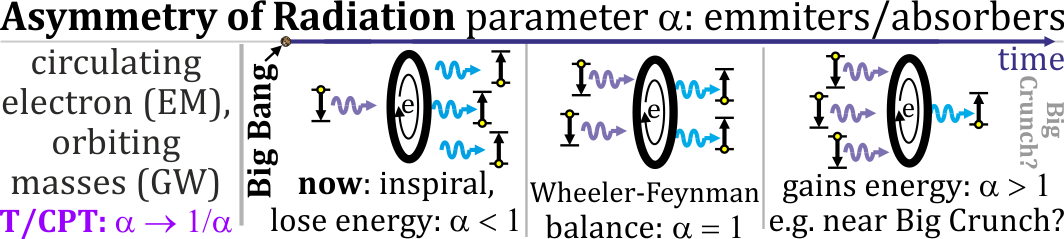
The Wheeler–Feynman absorber theory says both kinds could exist with equal weight (half retarded, half advanced). However, our universe seems to prefer retarded waves—objects like orbiting black holes lose energy and spiral inward (inspiral), which looks time-asymmetric.
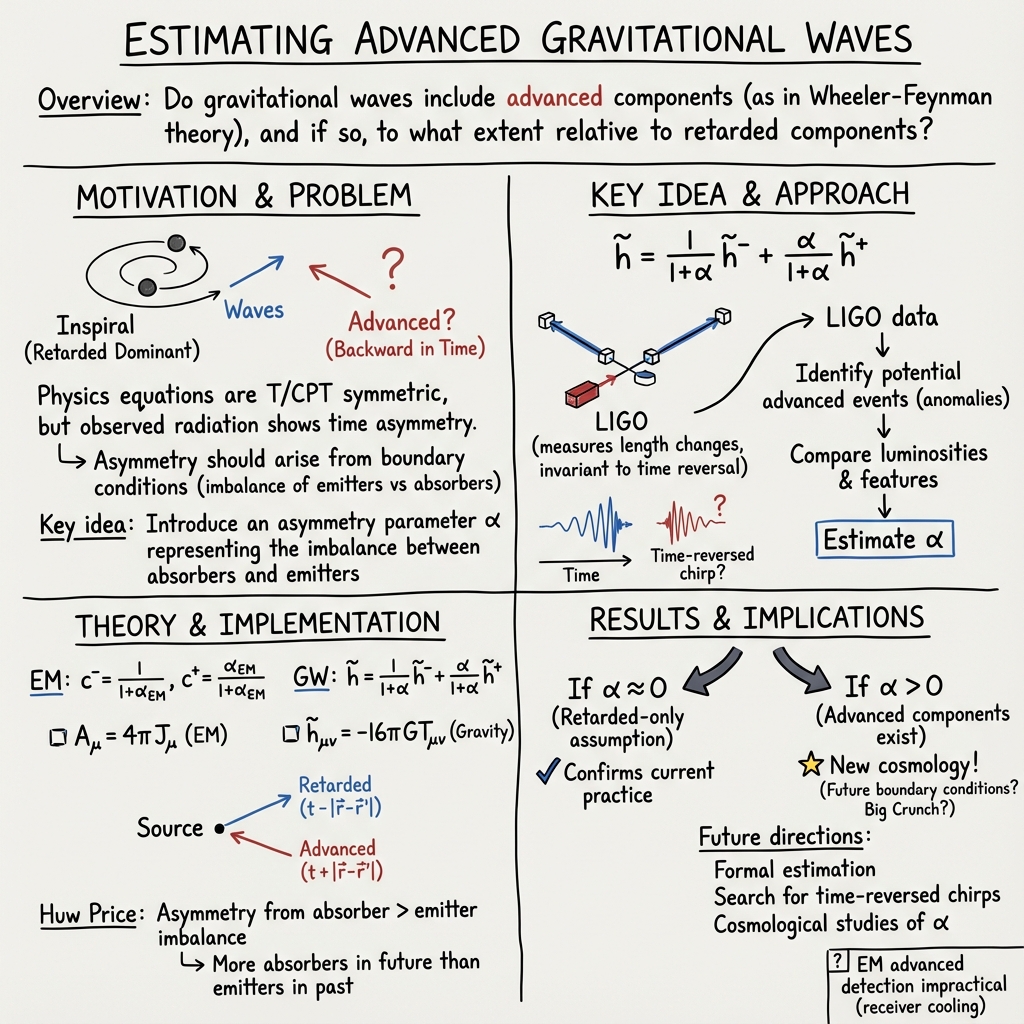
To capture this “preference,” the paper introduces a simple parameter α (alpha) that measures the imbalance:
- Retarded weight =
- Advanced weight =
If α = 0, it means “only retarded waves” (the current mainstream assumption). If α is small but not zero, advanced waves contribute a little.
Why look at gravitational waves? Regular electromagnetic detectors (like radio telescopes) are designed to absorb incoming signals and are not set up to “emit” in the time-reversed way you’d need to spot advanced waves. LIGO, however, essentially measures tiny changes in lengths, which should look the same even if time were reversed. That makes gravitational wave data a better place to test for a nonzero α.
Main ideas and suggested tests
The paper does not present new data analysis; instead, it proposes where and how to look for signs of advanced waves, or at least a small imbalance not captured by “retarded only.”
Here are the kinds of clues the author suggests checking:
- Missing electromagnetic partners in expected cases: Some gravitational-wave events (especially ones with neutron stars) should also produce light or other electromagnetic signals. If we find more and more cases where the EM counterpart is clearly required by the physics but is missing, an “advanced wave” explanation might be considered.
- Events that seem too early or too far: If an event looks like it happened at a time or distance that doesn’t make sense under current models (for example, black hole mergers in the “mass gap” that need more build-up time than the universe seems to allow), a small advanced contribution could ease that tension.
- Background “vibrations” of spacetime: Pulsar Timing Arrays have found a very low-frequency gravitational-wave background, likely from supermassive black hole pairs. If there aren’t enough known sources to explain it using retarded waves alone, allowing an advanced component might help.
The general plan: analyze many gravitational-wave events and try to estimate α from how strong the signals are, how often expected EM partners appear or don’t, and whether the population of sources matches what we observe. If α comes out zero, that supports the standard view. If α is small but positive, it suggests a tiny advanced-wave contribution.
Why this matters
If advanced waves contribute even a little, it would challenge the common belief that radiation only goes forward in time. That wouldn’t mean we can “see the future” in a sci-fi sense, but it would tell us something deep about how the universe’s past and future set the stage (the “boundary conditions”) for what we observe. It could:
- Refine our models of black hole mergers and the gravitational-wave background.
- Offer new tests of time symmetry (CPT symmetry) using cosmic observations.
- Motivate designing detectors and analyses that can spot subtle time-symmetric effects.
A simple conclusion and possible impact
The paper proposes a clear, testable idea: treat the mix of retarded and advanced waves as a dial (α) and try to measure it using gravitational waves. If α = 0, our current assumption stands strong. If α > 0 (even a tiny amount), we may need to include advanced waves in our thinking about the universe. That could impact how we interpret gravitational-wave signals, how we model cosmic events, and how we explore the deep connection between physics’ time-symmetric equations and our time-asymmetric experience.
To move forward, the author suggests:
- Careful statistical studies of existing and future gravitational-wave catalogs to estimate α.
- Targeted searches for unusual “chirp” shapes (signal patterns), including possible time-reversed ones.
- Simulations that respect time symmetry to see what kinds of signals should appear.
- Exploring how α might depend on frequency, direction, or the history of the universe.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of gaps and open questions that remain unresolved and would enable future researchers to make progress:
- Lack of a rigorous derivation of Wheeler–Feynman–style absorber theory for gravity: no formal extension to general relativity that handles nonlinearity, gauge freedom, radiation reaction, and physically admissible boundary conditions (absorber condition) in curved spacetimes.
- Ambiguity in the definition and placement of the asymmetry parameter α: unclear whether α weights metric perturbations, Green’s functions, energy flux, source dynamics, or detector response, and how this choice affects observables and conservation laws.
- Validity of convex combinations of advanced/retarded solutions in nonlinear GR: linearized approximations permit superposition, but compact-binary wave generation is inherently nonlinear; need to specify when and how mixture models remain physically consistent.
- Advanced solutions in curved cosmologies: absence of explicit advanced Green’s functions for FRW backgrounds and strong-field regions (near horizons), and of predictions for propagation, redshift, and phase evolution of advanced gravitational waves.
- Observable signatures of advanced contributions: no quantitative predictions for how strain time series, frequency–phase evolution, polarization content, memory effects, and sky localization would differ from purely retarded waveforms.
- Claim that interferometric “length measurements are T/CPT invariant” is untested: need hardware/software injection studies to quantify detector control-loop asymmetries, calibration nonidealities, and pipeline biases against time-reversed signals.
- Data-analysis methodology to estimate α is undeveloped: no matched-filter banks with time-reversed templates, no hierarchical Bayesian mixture models, no injection campaigns, and no selection-bias corrections tailored to advanced/retarded mixtures.
- Event classification criteria for “high probability of being advanced” are undefined: need operational rules, likelihood functions, and priors to assign per-event advanced probabilities based on waveform features, timing, and multi-messenger context.
- Missing EM counterpart argument lacks a quantitative framework: no model for counterpart detectability (beaming, attenuation, distance, instrument sensitivity, sky coverage), and no statistical test to separate “advanced-wave” hypotheses from mundane non-detections.
- “Too early” events and mass-gap mergers are interpreted without population synthesis: require rigorous hierarchical modeling including hierarchical growth, metallicity evolution, lensing magnification, and waveform systematics to test advanced contributions versus standard astrophysics.
- Redshift inference from GW-only data is not addressed: need methods (tidal signatures, population priors, lensing, cosmology) to estimate z and its uncertainties to evaluate “older than the Universe” claims without relying on rare EM counterparts.
- PTA background tension is not quantified under advanced-wave scenarios: missing population-level predictions for the stochastic background spectrum and amplitude when advanced contributions are included, and comparison with PTA constraints.
- Energy conservation and thermodynamic arrow issues are unresolved: no self-consistent treatment of radiation reaction with advanced components, risk of runaways/preacceleration, and unclear reconciliation with entropy increase and causal structure.
- Cosmological dependence of α is unspecified: no model for α(f, z, sky direction, polarization) tied to absorber/emitter densities, cosmic expansion history, or boundary conditions (e.g., Big Crunch versus accelerating expansion).
- “α reduces luminosity” claim is not derived: need formulas linking α to observable strain amplitude, energy flux, and inferred luminosity distance, with uncertainty propagation and per-event estimators.
- Gauge/coordinate invariance of the advanced–retarded decomposition is not demonstrated: require an invariant formulation (e.g., in terms of curvature perturbations) so α is not an artifact of gauge choice.
- Practical re-analysis plan of existing LIGO/Virgo/KAGRA catalogs is missing: define datasets, template banks (including reversed chirps), pipelines, quality vetoes, and expected sensitivity to α; set quantitative targets for exclusion or detection.
- Distinguishing advanced signatures from confounders is unaddressed: need tests against calibration errors, glitches, waveform-model biases (e.g., eccentricity, precession, higher modes), and gravitational lensing effects that can mimic atypical amplitudes/phases.
- Timing and causality consistency checks are not specified: if advanced signals imply source times “in the future,” devise multi-detector triangulation and multi-messenger protocols to test consistency without paradox (e.g., neutrinos, EM triggers, host galaxies).
- Advanced-wave templates for compact binaries are absent: develop PN/EOB/NR-based time-reversed waveform families, with clear prescriptions for radiation reaction and source dynamics under advanced boundary conditions.
- Definition of “emitters” and “absorbers” for gravitational radiation is vague: need an operational mapping to physical structures (e.g., compact objects, matter fields) and their cosmological number densities to connect α to measurable quantities.
- Electromagnetic test proposal is speculative and lacks design details: formulate a laboratory experiment with intentionally excited receivers to probe advanced EM waves, including required noise temperature, stimulation mechanisms, and feasibility analysis.
- Horizon and strong-field issues are ignored: advanced solutions may be non-unique or ill-posed near black-hole horizons; specify mathematical conditions and numerical schemes to handle time-reversed evolution across horizons.
- Polarization and memory predictions under advanced contributions are missing: quantify whether memory is reversed or modified and how polarization mixing would manifest in detector networks; propose measurable diagnostics.
- Statistical power requirements are not quantified: determine how many events, at what SNR and parameter diversity, are needed to constrain α below meaningful thresholds; include selection functions and catalog completeness.
- Integration with cosmological constraints is absent: if α ≠ 0, derive implications for energy budgets, CMB, BBN, and structure formation; identify existing datasets that could already bound α.
- Clear falsifiability criteria are lacking: define decisive tests (e.g., detection of robust reversed chirps) that would falsify or confirm nonzero α, with pre-registered analysis plans to avoid hindsight bias.
Glossary
- 4-current: The relativistic four-vector representing electric charge and current density in spacetime. "for 4-potential, 4-current, speed of light, and Lorentz gauge condition"
- 4-potential: The electromagnetic four-vector combining scalar and vector potentials. "for 4-potential, 4-current, speed of light, and Lorentz gauge condition"
- advanced EM waves: Electromagnetic solutions constructed with advanced (future-influenced) Green’s functions. "why we currently do not observe advanced EM waves: EM receivers are focused on absorption - of retarded wave."
- advanced waves: Field solutions determined by future boundary conditions (propagating backward in time in the advanced sense). "requirement to also include advanced waves into considerations."
- Asymmetry of Radiation: The imbalance in emission and absorption that makes retarded radiation dominate over advanced (or vice versa) due to boundary conditions. "Experimental estimation of such Asymmetry of Radiation is currently difficult for EM waves due to asymmetry between receivers and transmitters."
- asymmetry parameter α: A coefficient quantifying the imbalance between emitters and absorbers in radiation models. "We propose to denote their relation as coefficient to estimate it from gravitational wave data"
- Big Bang: The initial hot, dense state from which the Universe expanded. "The most known is entropy asymmetry of 2nd law of thermodynamics, e.g. as result of low entropy of Big Bang."
- Big Crunch: A hypothetical future collapse of the Universe back into a high-density state. "Huw Price~\cite{hp91} suggested natural looking solution of having more absorbers in our future (maybe with Big Crunch), than emitters in our past (with Big Bang)."
- chirp: The characteristic increase in frequency and amplitude of a gravitational-wave signal from inspiraling binaries. "having similar chirp shapes, but rather weaker luminosity"
- convex combinations: Weighted sums whose coefficients are nonnegative and sum to one, here combining retarded and advanced solutions. "their convex combinations are also solutions~\cite{rosen1979}:"
- CPT symmetry: Invariance under combined charge conjugation (C), parity inversion (P), and time reversal (T). "modern physics requires CPT symmetry~\cite{CPT}"
- EM counterpart: An electromagnetic signal associated with and corroborating a gravitational-wave event. "only one EM counterpart so far was observed (GW170817)."
- Feynman ensemble: The path-integral viewpoint of summing over all possible 4D histories (scenarios) for evolution. "and evolution calculated by Feynman ensemble of 4D scenarios."
- Gaussian units: A cgs-based unit system commonly used in theoretical electromagnetism. "Maxwell equations in Gaussian units for 4-potential, 4-current, speed of light, and Lorentz gauge condition"
- gravitational wave background: A stochastic background of gravitational waves from numerous unresolved sources. "gravitational wave background observed by MeerKAT Pulsar Timing Arrays"
- harmonic gauge condition: A gauge choice in linearized gravity requiring vanishing divergence of the trace-reversed metric perturbation. "being trace-reversed tensor satisfying harmonic gauge condition "
- hierarchical merging: Successive mergers of smaller compact objects to form more massive black holes. "Therefore, both initial black holes rather required some hierarchical merging"
- inspiraling: The inward spiral of orbiting bodies due to energy loss via radiation. "now we know they are inspiraling losing energy instead"
- least action principle: The principle that physical systems follow paths that extremize the action, yielding the field equations. "General relativity is already T-symmetric, solved by the least action principle"
- LIGO: The Laser Interferometer Gravitational-Wave Observatory detecting spacetime strain via precision length measurements. "e.g. LIGO just measures lengths, which are invariant to T/CPT symmetry"
- linearized general relativity: An approximation treating gravitational fields as small perturbations of flat spacetime to derive wave equations. "Analogously assuming linearized general relativity:"
- Lorentz gauge condition: A gauge in electromagnetism requiring the four-divergence of the four-potential to vanish. "and Lorentz gauge condition can be expressed as:"
- luminosity distance: A cosmological distance measure inferred from a source’s observed brightness. "directly estimated luminosity distance has already exceeded it, e.g. 27Gly for GW190403_051519"
- mass gap: A hypothesized range of black-hole masses that is absent due to stellar evolution constraints. "It is believed there is black hole mass gap for 50-120 solar mass"
- outspiraling: The increase of orbital separation over time (time-reversed inspiral) due to energy gain. "in T/CPT symmetry view they are gaining energy outspiraling instead"
- Pulsar Timing Arrays: Networks of precisely timed pulsars used to detect ultra-low-frequency gravitational waves. "observed by Pulsar Timing Arrays"
- redshift z: The fractional change in wavelength due to cosmic expansion, parameterized by z. "However, for real distance we need to divide it by for redshift ."
- retarded EM waves: Electromagnetic solutions determined by past sources (causal retarded Green’s functions). "Wheeler-Feynman absorber theory assumes there should be both retarded EM waves but also advanced"
- retarded waves: Field solutions determined by past boundary conditions, propagating forward in time. "the current default assumption is that , what should be verified experimentally." [context earlier: "1-0 contributions of only retarded waves"]
- S-matrix: The scattering matrix mapping initial states to final states in quantum field theory. "S-matrix "
- stimulated emission: Radiation emitted when an excited system is induced by an incident photon, central to lasers. "telescopes focused on (stimulated) emission"
- supermassive black holes (SMBH): Black holes with masses of millions to billions of solar masses. "binary supermassive black holes (SMBH)"
- T/CPT symmetry: Combined discussion of time-reversal and CPT invariance used to analyze symmetry of solutions. "As LIGO measures lengths, which are invariant to T/CPT symmetry"
- trace-reversed tensor: The modified metric perturbation used to simplify linearized Einstein equations. "being trace-reversed tensor"
- Wheeler-Feynman absorber theory: A time-symmetric radiation theory invoking both advanced and retarded interactions between emitters and absorbers. "Wheeler-Feynman absorber theory assumes there should be both retarded EM waves but also advanced"
Practical Applications
Immediate Applications
The following items describe practical, deployable uses of the paper’s findings and methods across sectors. Each item includes the sector, a specific use case, and potential tools/workflows, along with key assumptions/dependencies that affect feasibility.
- Academia (astronomy, cosmology): Re-analyze existing LIGO/Virgo/KAGRA catalogs to estimate an asymmetry parameter α (advanced vs retarded contribution) by fitting convex-combination waveforms h = (1/(1+α)) h_ret + (α/(1+α)) h_adv to event data; integrate α into Bayesian parameter estimation and model selection (compare α=0 vs α>0).
- Tools/workflows: Add α to PyCBC/Bilby/GstLAL template banks; run Bayes factors for α; event-level flags “advanced-compatible” when EM counterpart is strongly expected but absent.
- Assumptions/dependencies: Validity of linearized GR templates for both retarded and advanced solutions; SNR sufficient to distinguish α from source-parameter degeneracies; robust handling of selection effects and calibration uncertainties.
- Software industry (scientific computing, HPC, data platforms): Release an open-source “time-symmetric waveform” library and pipeline add-ons (Python/C++) that implement advanced-retarded convex combinations, time-reversed chirps, and α estimation; provide containers for reproducible runs on HPC/cloud.
- Tools/workflows: GitHub packages, Docker/Singularity images, CI-tested plugins for existing GW analysis stacks.
- Assumptions/dependencies: Community adoption, compatibility with current pipelines, documentation and benchmark datasets; computational cost for large-scale reprocessing.
- Academia + Consortia (PTA, gravitational-wave background): Extend PTA background models to include advanced-wave contributions; test whether including α improves fit to observed low-frequency “vibrations of the Universe” without requiring an unrealistically large SMBH population.
- Tools/workflows: Simulation modules in enterprise PTA packages; hierarchical Bayesian population inference with α as a nuisance or cosmological parameter.
- Assumptions/dependencies: Model identifiability (α vs SMBH population parameters); accuracy of PTA noise modeling; sufficient multi-year baselines.
- Observatory operations & policy (multi-messenger coordination): Update EM follow-up triage to introduce an “advanced-candidate” tag for GW events where EM counterparts are predicted but not observed after reasonable coverage; adjust expectations and resource allocation.
- Tools/workflows: Trigger-metadata fields for α fits, counterpart expectation checklists; decision trees for follow-up priority.
- Assumptions/dependencies: Clear criteria for “required EM counterpart”; risk of false positives; buy-in from collaborations and time-allocation committees.
- Academia (methods education): Incorporate absorber theory and time-symmetric reasoning into graduate coursework and seminars; create interactive exercises demonstrating retarded vs advanced solutions and α’s role.
- Tools/workflows: Jupyter notebooks, visualization apps, small student projects using public GW catalogs.
- Assumptions/dependencies: Access to curated datasets; instructor expertise; alignment with curricula.
- Catalog curation (data stewardship): Add α-fit summaries, “advanced-compatible” flags, and time-reversed-chirp search results to public GW event catalogs; support downstream reproducibility and meta-analyses.
- Tools/workflows: Schema extensions for catalog APIs (e.g., JSON/CSV fields), batch pipelines for periodic updates.
- Assumptions/dependencies: Event reprocessing agreements; versioning and provenance; standardized uncertainty reporting.
Long-Term Applications
The following items require additional research, scaling, or development before practical deployment.
- Instrumentation (electromagnetic observatories): Design and test EM receivers configured for controlled stimulated emission to probe time-symmetric scenarios (i.e., instruments capable of the “emission-focused” state needed to test advanced EM waves).
- Tools/products: Modified cryogenic sensor systems with tunable excitation, lab-scale time-symmetric optical/radio testbeds.
- Assumptions/dependencies: Feasibility of controlled initial excitation without compromising sensor stability; safety and regulatory compliance; theoretical clarity on observable signatures.
- Next-generation GW searches (signal processing): Develop template banks and real-time classifiers for time-reversed chirps and advanced-dominated signals; integrate α-dependent priors into low-latency pipelines for next-gen observatories (e.g., Cosmic Explorer, Einstein Telescope).
- Tools/workflows: ML-assisted template selection, dynamic priors for α(f, z, polarization), anomaly-detection modules tuned to advanced-like waveforms.
- Assumptions/dependencies: Improved sensitivity and bandwidth; reduction of glitch contamination; robust generalization beyond current noise environments.
- Cosmology (mapping absorber/emitter imbalance): Use measured α as a function of frequency, redshift, direction, and polarization to infer a “cosmic imbalance field” reflecting sources vs sinks across cosmic history; test Big Bang/Big Crunch boundary-condition hypotheses.
- Tools/workflows: Joint inference across GW catalogs, PTA datasets, and population synthesis; forward models in 4D spacetime “least action” simulations.
- Assumptions/dependencies: Sufficient event counts and redshift coverage; disentangling α from astrophysical evolution and selection biases; consistency across modalities (GW, EM).
- Multi-messenger strategy (ecosystem planning): Develop joint planning frameworks that incorporate the possibility of advanced contributions when interpreting missing counterparts, anomalous distances, or “too-early” events; update science cases and risk assessments.
- Tools/workflows: Cross-consortium playbooks; shared anomaly registries; policy briefs for TACs and funding agencies.
- Assumptions/dependencies: Demonstrated empirical benefits (e.g., improved fit or reduced paradoxes); coordination across global networks; acceptable cost-benefit.
- Standards & policy (research governance): Establish guidelines for reporting α estimates, advanced-candidate labels, and uncertainty disclosures; fund targeted programs for time-symmetry tests in GW/EM domains.
- Tools/workflows: Standards documents, workshop series, dedicated calls for proposals.
- Assumptions/dependencies: Consensus-building among stakeholders; clear metrics for success; sustained funding.
- Public engagement (science communication): Create visualizations and interactive experiences depicting time-symmetric physics, inspiral vs outspiral, and the role of advanced waves in explaining anomalies; support broader understanding of non-detections.
- Tools/products: VR/AR experiences, museum exhibits, media toolkits; classroom-ready simulations.
- Assumptions/dependencies: Evidence maturity to avoid misinformation; collaboration with educators and communicators.
Collections
Sign up for free to add this paper to one or more collections.