Counterexamples for FX Options Interpolations -- Part II (2512.19625v1)

Abstract: This follow-up article analyzes the impact of foreign exchange option interpolation on the vanilla option implied volatilities. In particular different exact interpolations of broker quotes may lead to different implied volatilities at the 10$Δ$ and 25$Δ$ Puts and Calls.

• The paper demonstrates that different interpolation methods yield significant discrepancies in FX option implied volatilities, even when exact market quotes are used.
• It outlines a rigorous calibration framework comparing dimension-2 versus dimension-5 objectives, emphasizing error propagation at key market points.
• It illustrates how the choice of interpolation method influences arbitrage potential and numerical stability, urging more robust, arbitrage-free parameterizations.

Analysis of FX Options Interpolation Pathologies

Introduction

The paper "Counterexamples for FX Options Interpolations -- Part II" (2512.19625) provides an in-depth exploration into the practical and numerical challenges of calibrating implied volatility surfaces for FX options. The study scrutinizes the effects of exact and approximate interpolations of broker FX option market quotes, particularly ATM, risk-reversal (RR), and butterfly (BF) volatilities quoted at specific $\Delta$ levels (10$\Delta$, 25$\Delta$ Puts and Calls). The work analyzes conventional calibration methodologies—including splines in log-moneyness, splines/polynomials in $\Delta$, SABR, and XSSVI—and highlights how these choices can result in non-negligible discrepancies in the reconstructed vanillas, especially under stressed or pathological market conditions.

Calibration Framework and Error Propagation

A central theme is the rigorous distinction between the market broker's quote convention (via composite spreads and strangles) and the generation of a smooth volatility function $\sigma(K)$. The broker convention requires recovery of vanillas at precise $\Delta$-strikes that generally do not coincide with quoted market strangles, and thus necessitates a non-linear system solution involving not only volatilities, but also $\Delta$-consistent strike conventions.

The iterative calibration pipeline is detailed, emphasizing decoupled (vanilla-only) versus joint (market strangle/vanilla/RR/ATM) error objectives. It is demonstrated that dimension-2 objectives, considering only strangle price errors, can result in significant misspecification at the ATM and RR points (absolute errors $>0.05$\% in ATM, up to $2.8$\% in 10$\Delta$ RR), as illustrated for EUR/HKD and EUR/TRY (Figure 1, Figure 2).

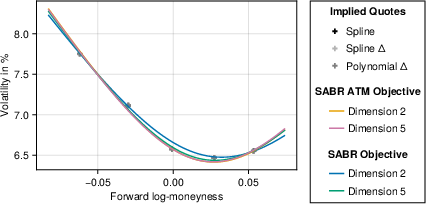
Figure 1: Vanilla implied volatilities for EUR/HKD 147 days options using SABR parameterization.

Figure 2: Vanilla implied volatilities for EUR/TRY 1y options under XSSVI calibration, highlighting errors in risk reversal matching.

The paper concludes that employing a dimension-5 calibration objective (incorporating ATM and RR errors in volatility terms, with vega-weighted price errors for strangles) provides materially improved fit at key market points and aligns the calibration outcome more closely with intuitive practitioner expectations.

Pathological Examples: Non-Uniqueness of Vanilla Outputs

A critical empirical finding is that, for volatile underlyings (e.g., EUR/TRY during heightened Turkish inflation), exact interpolation methods (e.g., cubic spline in log-moneyness, cubic spline in $\Delta$, polynomial in simple $\Delta$) yield significantly divergent implied vanilla volatilities, despite all being exact fits to the broker quotes. Figure 3 compellingly visualizes large divergence—particularly at far-from-ATM strikes—between these exact interpolations when calibrated to 2-year EUR/TRY data.

Figure 3: Exact interpolations calibrated to options on EUR/TRY expiring in 2 years, showing divergence between spline/polynomial approaches.

The robustness of specific parameterizations is further tested by fitting both SABR and XSSVI to these differently interpolated smiles (Figure 4), demonstrating that model-based fitting may or may not reinforce or attenuate the discrepancies seen in the vanillas, depending on both smile model and market regime.

Figure 4: SABR and XSSVI calibrated to vanilla implied quotes for EUR/TRY expiring in 2 years via log-moneyness spline and delta spline.

Manufactured Pathologies and Arbitrage Implications

By constructing synthetic broker quotes—specifically altering the spread and sign of RR components—the study exhibits that polynomial interpolation in $\Delta$ can generate highly oscillatory, non-financially meaningful volatility smiles (Figure 5). This example underlines that even arbitrage-free surface inputs may yield non-robust vanilla output if interpolation methodology is not carefully chosen and constrained.

Figure 5: Polynomial interpolation in $\Delta$ yields oscillatory implied volatility smile for manufactured EUR/TRY quotes.

Numerical and Theoretical Issues in $\Delta$ Inversion

The paper provides a technical analysis of the numerical pathologies that arise during strike-$\Delta$ inversion common in FX volatility surface construction. It is shown that call forward $\Delta$ with premium is non-monotonic as a function of strike for high volatilities and long maturities (Figure 6); in practical calibration, this may preclude direct mapping from $\Delta$ to strike for quoted 10$\Delta$ and 25$\Delta$ options—a non-trivial failure for calibration algorithms relying on root-finding near boundaries.

Figure 6: Call forward $\Delta$ with premium is non-monotonic in log-moneyness for high volatility regimes, peaking below 25\%.

Supplementary insights highlight edge cases:

• Iterative fixed-point or Newton’s methods can diverge or loop when seeking implied volatility for a fixed strike if the underlying polynomial/spline has inflection points or steep local slopes (Figure 7).
• Common SABR parameterizations with large vol-of-vol and high correlation can yield non-monotonic forward $\Delta$ profiles and associated arbitrage; the practical implication is that certain strikes may become unreachable (Figure 8).

Practical and Theoretical Implications

The empirical evidence suggests a trade-off between calibration precision and stability. While direct calibration to market quotes using complex, $\Delta$-based objectives can, in principle, minimize broker-quote errors, they introduce significant numerical risk, increased computational costs, and a propensity for non-robust, non-monotonic volatility surfaces. Conversely, vanilla calibration via exact interpolations (especially splines in log-moneyness) confers greater implementation stability and computational tractability, while generally yielding negligible error increases versus market quotes.

The finding that exact interpolations can be non-unique in terms of their effect on implied vanillas adds theoretical nuance to the literature, especially for illiquid regimes where smile shape is not fully supported by market data. It also motivates further research on regularization schemes for interpolation in $\Delta$-space and on the use of arbitrage-free parameterizations that guarantee monotonicity and reachability throughout the relevant strike range.

Conclusion

This study rigorously documents the sensitivities and potential pathologies emerging from conventional FX options smile calibration and broker quote interpolation practices. Strong numerical results underscore the importance of objective formulation and parameterization choice, with splines in log-moneyness generally providing the best trade-off between stability and market fidelity, while lower-dimensional objectives and unconstrained interpolants can yield substantial mismatches and implementation risk.

The practical implication is that vanilla interpolation followed by smooth parametric model fitting, constrained by broker conventions and monotonicity/arbitrage restrictions, is preferable for both robustness and computational efficiency. These insights are directly relevant for practitioners involved in real-world options desk calibration, as well as for theorists seeking to formalize arbitrage-free surface construction in the context of sparse, convention-dependent FX option markets.