Alternative positional encoding functions for neural transformers (2512.19323v1)
Abstract: A key module in neural transformer-based deep architectures is positional encoding. This module enables a suitable way to encode positional information as input for transformer neural layers. This success has been rooted in the use of sinusoidal functions of various frequencies, in order to capture recurrent patterns of differing typical periods. In this work, an alternative set of periodic functions is proposed for positional encoding. These functions preserve some key properties of sinusoidal ones, while they depart from them in fundamental ways. Some tentative experiments are reported, where the original sinusoidal version is substantially outperformed. This strongly suggests that the alternative functions may have a wider use in other transformer architectures.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
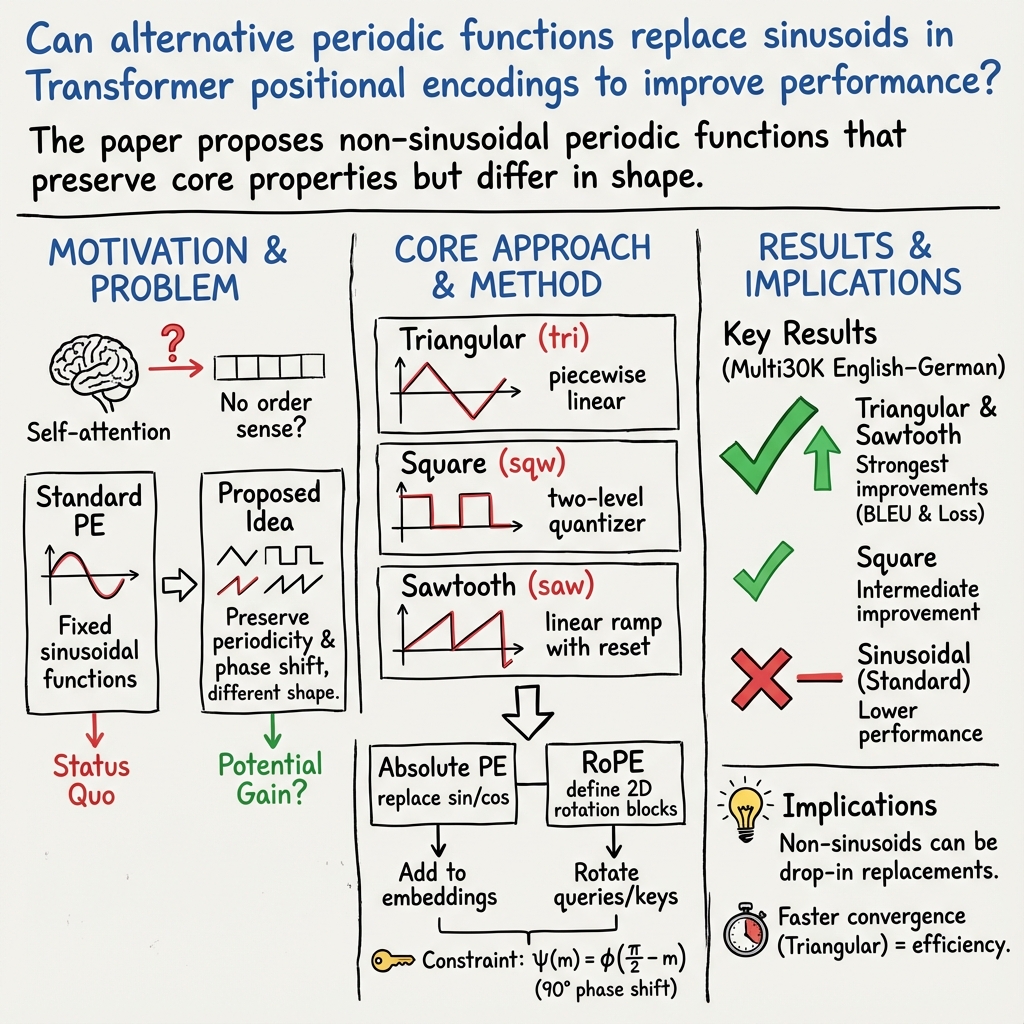
This paper looks at a key part of Transformer models (the kind of AI behind many language tools, like translation and chatbots) called positional encoding. Transformers are great at spotting relationships between words, but by default they don’t know the order of words. Positional encoding gives the model a way to tell “where” each word is in a sentence. The original method uses smooth, wavy math functions (sine and cosine). This paper tests new, alternative wave shapes—triangle, square, and sawtooth—to see if they can do better.
What questions does the paper ask?
The paper asks:
- Can we replace the usual sine and cosine waves used for positional encoding with other repeating (periodic) wave shapes?
- Do these alternative wave shapes help Transformers perform better, especially for language tasks like translation?
- Which wave shapes are the most effective and fastest to train?
How did the researchers approach the problem?
Key idea: Transformers need order
Transformers use a method called self-attention, which can look at all words at once. Without extra help, the model treats sentences like a bag of words—so “dog bites man” might look similar to “man bites dog.” Positional encoding adds a pattern to each word’s embedding (its numeric representation) so the model knows its position in order.
What is a “periodic function”?
A periodic function is a pattern that repeats over and over, like a wave. Sine and cosine are smooth waves. The paper keeps the idea of repeating waves but changes the shape.
The new wave shapes
To introduce the position of each word, the model adds numbers produced by one of these wave shapes (all repeat every , like sine/cosine), using a pair of “partner” waves that are shifted relative to each other (like sine and cosine are 90° out of sync). The paper tries:
- Triangle wave: ramps up linearly, then down, like a steady up-and-down saw motion.
- Square wave: switches sharply between two values, like an on/off switch.
- Sawtooth wave: steadily ramps up, then drops suddenly, repeating.
These shapes are chosen so they:
- repeat regularly (periodic), and
- come in pairs with the same shape but shifted, so they work nicely together in the model (similar to sine/cosine).
How they tested it
- Model: A standard “Transformer base” (the classic setup used in the original Attention Is All You Need paper).
- Task: English-to-German translation using the Multi30K dataset (short image captions and their translations).
- Training: They trained the same model many times using each wave shape for positional encoding.
- Fair comparison: 10-fold cross-validation (they split the data into 10 parts, trained on 9 parts and validated on the remaining part, rotating through all parts).
- Metrics:
- Loss (lower is better): This measures how wrong the model’s predictions are.
- BLEU-4 (higher is better): A standard translation score that checks how many overlapping word chunks match a reference translation.
What did they find and why is it important?
Main results
On average across the 10 runs:
- Sinusoidal (the original): BLEU-4 ≈ 29.5
- Triangle: BLEU-4 ≈ 40.7
- Square: BLEU-4 ≈ 34.5
- Sawtooth: BLEU-4 ≈ 40.8
Lower loss also matched the higher BLEU scores. The triangle and sawtooth waves clearly beat the traditional sine/cosine approach by a large margin on this task.
Why might these work better?
The paper suggests each wave shape has useful properties:
- Triangle wave: Its straight-line sections spread values more evenly and may make learning simpler and faster.
- Square wave: Acts like a quantizer (groups inputs into a few levels), which might enforce clear positional buckets.
- Sawtooth wave: Has a constant slope except for a jump, also spreading values evenly and helping the model track position changes.
In their experiments, triangle learned faster (reached good results sooner), while sawtooth achieved slightly higher top scores. Faster learning can mean less energy and time to train, which is very practical.
What does this mean going forward?
Implications
- Positional encoding isn’t “one-size-fits-all.” Changing the wave shape can significantly improve performance.
- Triangle and sawtooth waves might be strong default choices for translation tasks.
- Faster training (triangle) can save energy and time, which matters for big models and long experiments.
Caveats and next steps
- The tests were on one dataset (Multi30K), which is relatively small; more studies on bigger or different datasets (e.g., longer texts, other languages, code, audio) are needed.
- The approach should be tried in other Transformer variants (like those using rotary embeddings or relative positions) to see if benefits carry over.
- Exploring more wave shapes or combinations could yield further gains.
In short
Transformers need to know word order, and we usually give them that information using sine and cosine waves. This paper shows that swapping those waves for triangle or sawtooth waves can make translation models both better and, in some cases, quicker to train. That’s a simple change with a potentially big impact on how we build and train Transformer-based systems.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, actionable list of what remains missing, uncertain, or unexplored in the paper’s proposal of non‑sinusoidal positional encoding (PE) functions.
- External validity and scope:
- The empirical evaluation is limited to a single, small machine translation dataset (Multi30K) with word-level tokenization; results may not generalize to larger corpora (e.g., WMT14/16), subword tokenization (BPE/WordPiece), other NLP tasks (language modeling, summarization, code), or other modalities (vision, speech, time-series).
- Only absolute input-level positional encodings were tested; the paper does not compare against modern baselines such as learned absolute embeddings, RoPE, ALiBi, relative PEs (Shaw et al.), or kernelized methods (KERPLE).
- Length generalization:
- No experiments assess extrapolation to sequences longer than those seen during training; it is unknown whether triangular, square, or sawtooth functions retain or improve length generalization relative to sinusoidal, RoPE, ALiBi, or KERPLE.
- The impact of non‑sinusoidal PE on long-range dependency tasks (e.g., LRA benchmarks) remains untested.
- Theoretical guarantees for RoPE-like use:
- The proposed replacement of
sin/coswith arbitrary periodicφ/ψin rotation matrices is not theoretically validated; key properties required by RoPE are not addressed: - Orthogonality/unitarity: rotation matrices require
φ(θ)^2 + ψ(θ)^2 = 1and norm preservation; this is generally violated by the proposed functions. - Angle additivity/group structure:
R(θ_1) R(θ_2) = R(θ_1 + θ_2)depends on trigonometric addition identities, which do not hold for triangular/square/sawtooth waves. - Relative position dependence: formal proof that attention logits depend only on
m − nunder non‑sinusoidal rotations is missing. - If the non‑sinusoidal functions are to be used within RoPE or relative schemes, derive necessary and sufficient conditions on
φ,ψ(e.g., boundedness, normalization, addition law, norm preservation) and validate them empirically.
- The proposed replacement of
- Phase-shift construction:
- The paper imposes
ψ(m) = φ(π/2 − m)but does not justify that this yields the desired “quadrature” relationship for non‑sinusoidal functions (e.g., square or sawtooth); clarify the mathematical rationale and whether an alternativeψis needed to ensure orthogonality/complementarity.
- The paper imposes
- Amplitude and scaling confounds:
- The waveforms have very different output ranges (e.g.,
saw ∈ [−2π, π],tri ∈ [−2, 2],sqw ∈ {−1, 1}), potentially changing the effective magnitude of PE components and overshadowing token embeddings; results may reflect scale effects rather than functional form. - Conduct ablations with amplitude normalization (e.g., rescaling to unit variance per dimension) and controlled per-frequency magnitudes to isolate the effect of waveform shape.
- The waveforms have very different output ranges (e.g.,
- Frequency schedule and spectral properties:
- Non‑sinusoidal functions introduce rich harmonic content; the interaction between the exponential frequency schedule and higher harmonics is not analyzed (aliasing, positional collisions, spurious periodicities).
- Provide a spectral analysis (Fourier decomposition) of the encodings and study how harmonic overlap affects positional uniqueness, attention logits, and optimization.
- Positional uniqueness and collisions:
- Square wave encodings collapse many positions to identical values (binary outputs per dimension), risking positional collisions; quantify collision rates across positions/dimensions and their effect on attention and performance.
- Explore multi-phase square waves, adjustable duty cycles, or composite encodings to increase positional distinguishability.
- Injection point and compatibility:
- Only input-level addition was evaluated; investigate injecting the proposed functions inside attention (biasing logits), hybrid schemes, and post-attention variants, and compare across injection points.
- Robustness, sensitivity, and statistical testing:
- No multi-seed runs or statistical significance tests are reported; assess sensitivity to random initialization, data shuffles, and hyperparameters (learning rate/schedule, batch size, dropout, max length).
- Report confidence intervals and significance when claiming improvements; include standardized evaluation on official dev/test splits rather than CV on the training split.
- Training efficiency and energy claims:
- The paper claims faster learning for triangular PE and potential energy savings but does not report wall‑clock time, FLOPs, or energy consumption; measure and compare convergence speed (epochs/steps to plateau), compute, and energy across encodings.
- Numerical stability and optimization behavior:
- Discontinuous or non‑smooth encodings (square/sawtooth) may affect gradient distributions or attention logits; analyze norm preservation, logit scale, and gradient statistics to detect instability or exploding/vanishing behaviors.
- Model scaling and architecture diversity:
- Results are for a base Transformer with
d_model = 512; evaluate across model sizes (small to large), number of heads,d_ff, and depth; test decoder‑only LLMs (e.g., LLaMA‑style models) that rely on RoPE. - Assess compatibility with tied embeddings, shared projections, and mixed-precision training.
- Results are for a base Transformer with
- Tokenization and preprocessing:
- Verify whether improvements persist with subword tokenization (BPE/SentencePiece), case preservation, and different vocabulary thresholds; assess OOV handling and its interaction with PE.
- Cross‑modality and downstream tasks:
- Test on vision (ViT), audio/speech (ASR), and time‑series forecasting, where positional/temporal inductive biases differ; evaluate task-specific benefits and failure modes.
- Learnable or parameterized waveforms:
- Investigate parameterized families (e.g., duty cycle for square, slope/offset for saw/triangle), learnable mixtures of basis functions, or Fourier series coefficients learned end‑to‑end; compare fixed vs learnable non‑sinusoidal encodings.
- Per‑head/per‑dimension heterogeneity:
- Explore using different waveforms or parameters across attention heads or dimensions; study whether heterogeneity improves representational capacity or stability.
- Frequency spacing design:
- Justify whether exponential spacing remains optimal for non‑sinusoidal functions; compare linear/logarithmic spacing or task‑adaptive schedules; potentially learn per‑dimension frequencies.
- Attention interpretability:
- Provide qualitative analyses (attention maps, probe tasks) to show how non‑sinusoidal PEs influence the model’s use of positional information (e.g., locality bias, periodic patterns, shift invariance).
- Implementation clarity and reproducibility:
- Specify seeds, exact commit hashes, and configuration files; ensure evaluation on standardized splits; provide instructions to reproduce the reported results and figures with identical settings.
- Computational overhead:
- Benchmark the cost of computing piecewise functions vs
sin/coson CPU/GPU; evaluate vectorization and branchless implementations; quantify any speedups or slowdowns.
- Benchmark the cost of computing piecewise functions vs
- Safety and artifacts:
- Examine whether strong periodic patterns induce undesired artifacts (e.g., translation rhythm, repetition) or bias the model toward certain positional intervals; design stress tests to detect such behaviors.
- Formal connection to relative methods:
- Beyond RoPE, analyze whether and how non‑sinusoidal functions can be incorporated into learned relative bias frameworks (e.g., Shaw et al., KERPLE) without violating conditional positive definiteness or probabilistic attention interpretations.
Glossary
- Absolute positional encodings: Vectors assigned to each position index and combined with token embeddings to encode order. "Absolute positional encodings assign each sequence index a dedicated vector that is combined with token embeddings, for instance via elementwise addition"
- Adam optimizer: A first-order stochastic optimization algorithm using adaptive learning rates. "Models were trained using the Adam optimizer"
- Attention heads: Multiple parallel attention mechanisms within a layer to capture diverse patterns. "h = 8 attention heads"
- Attention logits: Pre-softmax scores in the attention mechanism that determine weighting of keys for each query. "In these models, attention logits are augmented with terms that depend on the relative offset of query and key positions,"
- Attention manipulation: Methods that inject positional information directly into attention computations. "position embeddings, attention manipulation, and hybrid schemes"
- Attention scores: The normalized weights (typically after softmax) that determine how much each token attends to others. "incorporated into the attention scores in a way that preserves the probabilistic interpretation of self-attention"
- BLEU-4: An n-gram based evaluation metric for machine translation using up to 4-grams. "we report the final training/validation loss and BLEU-4 after the last epoch,"
- Block-diagonal: A matrix structure composed of square blocks along the diagonal with zeros elsewhere. "where is block-diagonal with 2D rotations along the diagonal."
- Conditionally positive definite kernels: Kernel functions satisfying conditional positive definiteness, used to encode relative distances. "distances between positions are mapped through conditionally positive definite kernels,"
- Cross-entropy loss: A loss function measuring the difference between predicted probability distributions and true labels. "training used cross-entropy loss with padding tokens ignored."
- Cross-validation (10-fold): A resampling method that partitions data into 10 folds to assess generalization. "we employed 10--fold cross--validation"
- Dropout probability: The fraction of units randomly zeroed during training to prevent overfitting. "a dropout probability of 0.1 applied to all sub--layers."
- Exponentially spaced frequencies: Frequency components increasing exponentially, used in sinusoidal positional encodings. "The choice of exponentially spaced frequencies allows the model to represent relative offsets as approximately linear functions of the encodings and to extrapolate to longer sequences."
- Gradient clipping: A technique that limits gradient norms to stabilize training. "Gradients were clipped to a maximum norm of 1.0,"
- Hybrid schemes: Approaches that inject position information at multiple points (e.g., embeddings and attention). "position embeddings, attention manipulation, and hybrid schemes"
- Inductive bias: Assumptions built into a model that guide learning and generalization. "The design of positional encoding has emerged as a central inductive bias that strongly affects performance, robustness, and length generalization"
- Kernelized relative positional embeddings: Relative positional encoding functions defined via kernels to improve extrapolation. "A prominent recent line of work develops kernelized relative positional embeddings for length extrapolation"
- Key vector: In attention, the representation associated with each token used to compute compatibility with queries. "Consider a per-head query $\bm{q}_{m}\in\mathbb{R}^{d_{k}$ and key $\bm{k}_{n}\in\mathbb{R}^{d_{k}$ at positions and ."
- Length extrapolation: The ability of models to handle sequences longer than those seen in training. "kernelized relative positional embeddings for length extrapolation"
- Length generalization: Model robustness to different sequence lengths without retraining. "strongly affects performance, robustness, and length generalization"
- Learning rate: The step size used by optimization algorithms to update parameters. "The learning rate was automatically decayed based on validation performance."
- Permutation-invariant: A property where output does not change when input elements are reordered. "self-attention operation is permutation-invariant"
- Position embeddings: Learned or fixed vectors added to token embeddings to encode position. "position embeddings, attention manipulation, and hybrid schemes"
- Positional encoding (PE): Mechanisms that inject order information into Transformer models. "positional encoding (PE) mechanisms inject information about token positions, either as absolute indices or as relative distances between tokens"
- Position-wise feed-forward networks: Fully connected networks applied independently to each position in a sequence. "A standard Transformer layer applies content-based self-attention followed by position-wise feed-forward networks,"
- Probabilistic interpretation of self-attention: Viewing attention weights as probability distributions over keys for each query. "preserves the probabilistic interpretation of self-attention"
- Query vector: In attention, the representation that seeks relevant information from keys/values. "Consider a per-head query $\bm{q}_{m}\in\mathbb{R}^{d_{k}$ and key $\bm{k}_{n}\in\mathbb{R}^{d_{k}$ at positions and ."
- Relative positional encodings: Methods encoding distances between token pairs directly in attention. "Relative positional encodings instead represent the distance between token pairs and inject this information directly into the attention computation"
- Rotary Positional Embedding (RoPE): A positional scheme that rotates queries and keys so their inner product reflects relative position. "Rotary Positional Embedding (RoPE) encodes positions by rotating query and key vectors in a shared complex (or 2D) subspace, so that their inner product depends on relative position"
- Self-attention: Mechanism where tokens attend to others in the same sequence to compute contextualized representations. "A standard Transformer layer applies content-based self-attention followed by position-wise feed-forward networks,"
- Token embeddings: Dense vector representations of discrete tokens used as model inputs. "The encoding is then added to the token embeddings ,"
- Weight decay: L2 regularization added to the loss to penalize large weights. "weight decay of ."
Practical Applications
Below is an overview of practical, real-world applications suggested by the paper’s findings and methods, organized by deployment horizon. Each item notes sectors, concrete use cases, potential tools/products/workflows, and key assumptions or dependencies.
Immediate Applications
These are deployable now with modest engineering effort, leveraging the paper’s open-source implementation and inutile changes to model architecture.
- NLP machine translation quality boosts and faster training
- Sectors: software, education, media/localization
- Use cases: improve BLEU and reduce training time for in-house or SaaS translation systems, academic MT benchmarks, educational content localization
- Tools/products/workflows:
- Swap sinusoidal PE with triangular or sawtooth PE in Transformer-base or seq2seq models using PyTorch/Hugging Face Transformers
- Integrate into existing training pipelines (e.g., Fairseq, OpenNMT, Hugging Face) as a drop-in PositionalEncoding module
- Provide an MLOps “PE type” hyperparameter (sin/tri/saw/sqw) in experiment configs
- Assumptions/dependencies:
- Reported gains are on Multi30K English–German; performance may vary with language pairs, tokenization (subword vs word), scale, and domain
- Frequency schedule (e.g., 100002i/d_model) is retained; changes may alter behavior
- Discontinuous functions (square/saw) trained stably in the paper but should be re-validated for other datasets
- Energy/carbon reduction during model training
- Sectors: energy, sustainability, enterprise AI
- Use cases: reduce GPU-hours and cost by converging faster with triangular PE while retaining competitive quality
- Tools/products/workflows:
- Add “green training” preset selecting triangular PE and early stopping when BLEU plateaus
- Track energy/kWh and CO2e in experiment dashboards to quantify savings
- Assumptions/dependencies:
- Convergence-speed advantage persists beyond the reported setup
- Savings depend on dataset size, hardware, and training regimes
- Rapid ablation studies in academic research on positional encodings
- Sectors: academia
- Use cases: study generalization, length extrapolation, and training dynamics by swapping φ/ψ functions
- Tools/products/workflows:
- Use the provided GitHub repo to replicate and extend to benchmarks (e.g., WMT, IWSLT)
- Add AutoML sweeps over PE types and phase shifts
- Assumptions/dependencies:
- Results may differ on relative PE baselines (ALiBi, KERPLE) and larger corpora
- Drop-in experimentation with RoPE-based models
- Sectors: software (LLM training/fine-tuning), open-source LLMs
- Use cases: substitute non-sinusoidal φ/ψ in rotary embeddings to test effects on fine-tuning tasks (summarization, instruction tuning)
- Tools/products/workflows:
- Modify RoPE kernels in frameworks (e.g., xformers, FlashAttention-compatible code) to use triangular/sawtooth φ with phase-shifted ψ
- Evaluate downstream metrics (e.g., Rouge, MMLU subsets) in fine-tunes
- Assumptions/dependencies:
- RoPE substitution preserves relative-position properties with the paper’s phase-shift constraint
- Needs careful benchmarking for long-context behavior
- On-device and edge NLP where compute simplicity matters
- Sectors: mobile/embedded, consumer software
- Use cases: on-device translation, predictive text, small Transformers where simpler piecewise-linear φ/ψ can reduce compute overhead
- Tools/products/workflows:
- Replace runtime sin/cos with piecewise-linear calculations or small look-up tables for φ/ψ
- Package as a lightweight library for mobile inference
- Assumptions/dependencies:
- PE compute cost is a small fraction of total inference; benefits are marginal unless trigonometric intrinsics are a bottleneck on specific hardware
- Accuracy trade-offs must be measured per application
- Curriculum and classroom demos to teach positional encoding
- Sectors: education
- Use cases: hands-on labs contrasting sinusoidal vs non-sinusoidal PEs for learning dynamics and error analysis
- Tools/products/workflows:
- Jupyter notebooks integrating the repo; visualizations of training curves and BLEU
- Assumptions/dependencies:
- None beyond standard ML course infrastructure
- Domain-specific prototype trials beyond MT
- Sectors: healthcare, finance, robotics, speech
- Use cases: pilot tests in:
- Healthcare: clinical note summarization/translation (e.g., discharge summaries)
- Finance: news-to-signal summarization, document QA
- Robotics: instruction-to-action translation, trajectory sequence modeling
- Speech: ASR/translation with Transformer decoders
- Tools/products/workflows:
- Fine-tune existing Transformer-based models substituting PE, monitor task metrics and convergence
- Assumptions/dependencies:
- Effects can differ for modalities that already use relative PEs or learned 2D/temporal encodings
- Regulatory/PII constraints apply in healthcare/finance pilots
Long-Term Applications
These require additional validation at scale, integration with large models, or adjustments to broader ecosystems.
- Integration into large-scale pretraining of LLMs and multimodal models
- Sectors: software, media, enterprise AI
- Use cases: replace sinusoidal/standard RoPE with triangular/sawtooth variants during pretraining to target better quality-per-flop or faster convergence
- Tools/products/workflows:
- Pretraining trials on open corpora (e.g., The Pile, RedPajama) with matched budgets
- Evaluate long-context tasks, chat quality, grounding, and safety metrics
- Assumptions/dependencies:
- Scaling laws with non-sinusoidal PEs remain favorable
- Long-context stability and retrieval must be preserved; extensive ablations needed
- Task-tailored PE design and AutoPE search
- Sectors: software, AutoML platforms, vertical AI solutions
- Use cases: learn or search over parameterized periodic functions (including quantizing square waves) for domains with discrete or bursty temporal structure (e.g., logs, events)
- Tools/products/workflows:
- Add a “PE function family” in AutoML (tri/saw/sqw + learnable slopes, duty cycles)
- Meta-learning/scheduling PE types across training phases
- Assumptions/dependencies:
- Generalization doesn’t degrade when tuning φ/ψ beyond fixed defaults
- Optimization remains stable with discontinuities
- Long-context and memory-intensive applications with modified rotary embeddings
- Sectors: legal, R&D, customer support
- Use cases: document QA, long-form summarization, code completion with contexts >100k tokens using non-sinusoidal RoPE variants
- Tools/products/workflows:
- Couple modified RoPE with long-context tricks (position interpolation, NTK-aware scaling)
- Evaluate on LongBench/Needle-in-a-Haystack, code benchmarks
- Assumptions/dependencies:
- Non-sinusoidal φ/ψ maintain or improve interpolation/extrapolation behavior
- Interactions with KV-caching and attention scaling are benign
- Vision and audio Transformers with alternative absolute or hybrid PEs
- Sectors: healthcare (medical imaging), autonomous systems, media
- Use cases:
- ViTs at higher input resolutions; medical image report generation where patch order signals matter
- Audio/speech Transformers for diarization, music modeling
- Tools/products/workflows:
- Replace learned absolute PEs or hybrid schemes with periodic triangular/sawtooth variants; probe robustness to resolution/length shifts
- Assumptions/dependencies:
- Many SOTA ViTs favor learned or relative PEs; gains from periodic alternatives must be demonstrated
- 2D extensions (separable φ/ψ per axis) need careful design
- Hardware and kernel-level optimization for PE computation
- Sectors: semiconductors, cloud AI
- Use cases: implement piecewise-linear φ/ψ in GPU/TPU kernels to avoid trig functions, improving throughput in training/fine-tuning at scale
- Tools/products/workflows:
- Custom CUDA kernels or fused ops for PE + embedding addition + dropout
- Vendor libraries offering “fast-PE” paths
- Assumptions/dependencies:
- Overall speedups materialize in real workloads (PE often a small fraction of runtime)
- Kernel fusion opportunities outweigh integration complexity
- Green AI policies and reporting standards incorporating low-energy PE
- Sectors: policy, enterprise governance, sustainability reporting
- Use cases: include PE choice in “energy-efficient ML” best practices and procurement criteria
- Tools/products/workflows:
- Mandate reporting of PE type and energy per achieved metric (e.g., BLEU@X)
- Assumptions/dependencies:
- Wider empirical evidence of energy/quality benefits across tasks and scales
- Safety/robustness and OOD generalization research
- Sectors: academia, high-stakes AI (healthcare, finance)
- Use cases: investigate whether quantized (square) or uniform-slope (tri/saw) PEs affect adversarial susceptibility, spurious length biases, or OOD degradation
- Tools/products/workflows:
- Robustness suites for sequence models; targeted perturbation tests
- Assumptions/dependencies:
- Benefits are uncertain and require systematic study; may vary by task and model size
- Workflow innovation: dynamic PE scheduling
- Sectors: software, MLOps
- Use cases: start training with triangular PE for fast convergence; switch to sawtooth for peak quality; or mix across layers/heads
- Tools/products/workflows:
- Callback APIs in PyTorch/TF to hot-swap PE functions at milestones
- Layer-wise heterogeneous PE configurations
- Assumptions/dependencies:
- Switching PEs mid-training does not destabilize optimization
- Requires validation per architecture
In summary, the paper’s main actionable insight is that replacing sinusoidal positional encodings with triangular or sawtooth functions can substantially improve MT performance and reduce training time in a standard Transformer setup. This invites immediate trials in translation and fine-tuning workflows and motivates longer-term exploration in large-scale pretraining, long-context models, and hardware/software co-design aimed at energy-efficient transformers.
Collections
Sign up for free to add this paper to one or more collections.