Spherical Leech Quantization for Visual Tokenization and Generation (2512.14697v1)

Abstract: Non-parametric quantization has received much attention due to its efficiency on parameters and scalability to a large codebook. In this paper, we present a unified formulation of different non-parametric quantization methods through the lens of lattice coding. The geometry of lattice codes explains the necessity of auxiliary loss terms when training auto-encoders with certain existing lookup-free quantization variants such as BSQ. As a step forward, we explore a few possible candidates, including random lattices, generalized Fibonacci lattices, and densest sphere packing lattices. Among all, we find the Leech lattice-based quantization method, which is dubbed as Spherical Leech Quantization ($Λ_{24}$-SQ), leads to both a simplified training recipe and an improved reconstruction-compression tradeoff thanks to its high symmetry and even distribution on the hypersphere. In image tokenization and compression tasks, this quantization approach achieves better reconstruction quality across all metrics than BSQ, the best prior art, while consuming slightly fewer bits. The improvement also extends to state-of-the-art auto-regressive image generation frameworks.

• The paper introduces Spherical Leech Quantization (SLQ) which employs the 24D Leech lattice as a fixed, non-parametric visual codebook.
• SLQ unifies various NPQ methods through lattice coding, revealing intrinsic links between entropy regularization, dispersiveness, and quantization quality.
• Empirical results show SLQ achieving state-of-the-art performance in image reconstruction, compression, and autoregressive generation with large codebooks.

Spherical Leech Quantization for Visual Tokenization and Generation

Introduction

The paper "Spherical Leech Quantization for Visual Tokenization and Generation" (2512.14697) investigates the limits of non-parametric quantization (NPQ) for visual tokenizers, focusing on scaling visual codebooks up to $\sim$200,000 discrete atoms while ensuring efficient and principled learning. The main contribution is the formulation of Spherical Leech Quantization (SLQ), which utilizes the first shell of the 24-dimensional Leech lattice—a structure known to achieve the densest sphere packing in 24D space—as a fixed, non-learnable codebook for visual quantization. The core insights are geometric: existing NPQ methods can be unified through the lens of lattice coding, revealing intrinsic connections between entropy regularization, dispersiveness, and quantization quality. Leveraging the extreme symmetry and uniformity of the Leech lattice, SLQ achieves state-of-the-art (SOTA) performance in visual compression, reconstruction, and generation tasks, with a radically simplified, regularization-free training objective.

Unifying Non-Parametric Quantization with Lattice Coding

The paper provides a geometric abstraction where various NPQ approaches—Lookup-Free Quantization (LFQ), Binary Spherical Quantization (BSQ), Finite Scalar Quantization (FSQ), and Random Projection Quantization (RPQ)—are all formulated as lattice codes. Each quantizer corresponds to a lattice (typically with constraints enforcing bounded norm, occupancy, or binarization), and the quantization process is interpreted as a lattice point search in the appropriate geometric domain.

Critically, codebook utilization and the avoidance of collapse are closely tied to the dispersiveness of codewords—measured by the minimum pairwise distance, $\delta_\mathrm{min}$, between codewords on the hypersphere. The theoretic connection between entropy regularization and sphere packing emerges naturally: entropy maximization corresponds to finding the most uniformly spread configuration of points (codes) on the sphere, which is mathematically equivalent to maximizing $\delta_\mathrm{min}$ for a given codebook size.

Figure 1: $d=3$. Illustrative geometry of sphere packing lattices compared to NPQ codebooks.

Densest Packing, The Leech Lattice, and Spherical Leech Quantization

The design of SLQ proceeds by selecting the unique, optimal 24-dimensional Leech lattice $\mathbb{\Lambda}_{24}$, whose first shell contains 196,560 points equidistant from the origin, representing the densest known sphere packing in $d=24$. By normalizing these lattice vectors, each codebook entry corresponds to a unit vector on $S^{23}$, ensuring maximum pairwise separation and uniformity. This configuration dramatically increases $\delta_\mathrm{min}$ over alternatives like BSQ, e.g., $\delta_\mathrm{min,B}$SQ$=0.471$, $\delta_\mathrm{min,SLQ}=0.866$ for codebooks of comparable size.

From the training standpoint, SLQ is non-parametric and requires no entropy regularization or commitment loss: the extreme symmetry of the codebook inherently maximizes utilization and avoids collapse, supporting direct use of simple autoencoding objectives. This results in both more robust optimization and parameter/memory efficiency, since there are no learnable codebook vectors.

Figure 2: VF alignment improves convergence and final generation results, especially recall.

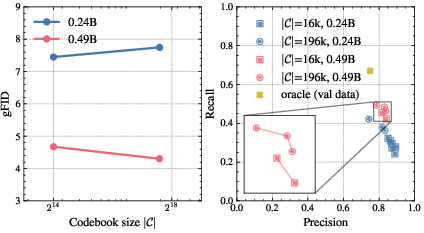
Figure 3: Scaling effect of the codebook size.

Empirical Evaluation

Image Reconstruction and Compression

SLQ-based visual tokenizers outperform previous methods, such as BSQ and VQ-based tokenizers, across all pertinent metrics on COCO2017, ImageNet-1K, and the Kodak compression benchmark. Specifically, SLQ autoencoders push the rate-distortion boundary, achieving an rFID of 0.83 (down from 1.14 for BSQ) at comparable or lower bitrates (effective $d^\star=17.58$, vs $d=18$ for BSQ). In absolute terms, PSNR and MS-SSIM are also higher than prior art while reducing model complexity and auxiliary loss design.

Autoregressive Visual Generation at Scale

Autoregressive image generation models built with SLQ tokenizers (specifically integrated into the Infinity and VAR backbones) are shown to scale gracefully to 200K codebooks—a regime matching the vocabulary size of LLMs, but previously unattainable for visual AR models without architectural or training "tricks" (no index subgrouping, multi-head predictions, or bitwise corrections are used). The achieved generation FID is 1.82 (against an oracle validation FID of 1.78) on ImageNet-1K, with improved recall and precision. Grid search studies and ablations further demonstrate that larger codebooks yield better precision-recall characteristic curves only once the underlying model is sufficiently large, mirroring the macro scaling laws observed in LLMs.

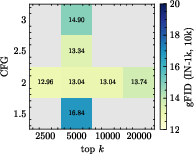
Figure 4: BSQ + BCE; grid search of sampling parameters shows optimal $k$ varies strongly with codebook and head settings.

Figure 5: More sampled generation results of Infinity-CC + (2B). SLQ enables both high visual fidelity and a diversity that tracks the improvement in codebook scaling.

Theoretical and Practical Implications

The lattice-coding view of NPQ provides a principled path to codebook design for visual tokenization. It highlights that maximizing uniformity and symmetry in code distribution can fully obviate ad-hoc regularization, especially at large vocabulary sizes. The demonstration that the Leech lattice supports efficient, parameter- and memory-light quantization for both autoencoding and AR modeling suggests that geometric approaches will generalize well to not only images and videos but also settings demanding high-cardinality symbolic representations.

On the practical side, the combination of SLQ with advanced sampling and loss functions (like VF alignment, classifier-free guidance, and large-scale optimizer stabilization) enables direct scaling to the regime previously thought possible only for LLMs. SLQ's fixed, highly-dispersive representation also admits efficient hardware implementation, low-bitrate lossy compression codecs, and potential integration with multi-modal AR and generative models.

Future Directions

Potential avenues include:

• Extending SLQ beyond $d=24$, via shell-union or higher-dimensional lattices, to push codebook size and dispersiveness.
• Investigating SLQ for tokenization in multi-modal and text-conditioned generation, leveraging its high cardinality and uniformity.
• Integrating SLQ with compositional or hierarchical generative architectures exploiting structured codebook geometry.
• Adapting similar geometric lattice-based codebooks in domains outside vision, e.g., speech tokenization, molecular graph encoding.

Conclusion

Spherical Leech Quantization establishes a new standard for codebook design in visual tokenization, demonstrating that the intersection of geometric lattice theory and deep learning provides both theoretical clarity and substantial empirical improvement. SLQ's ability to achieve SOTA results with model and training simplicity, and scale to LLM-class vocabulary sizes without codebook collapse, opens clear paths toward the next generation of high-fidelity, large-scale discrete generative modeling (2512.14697).