A Geometric Theory of Cognition (2512.12225v1)

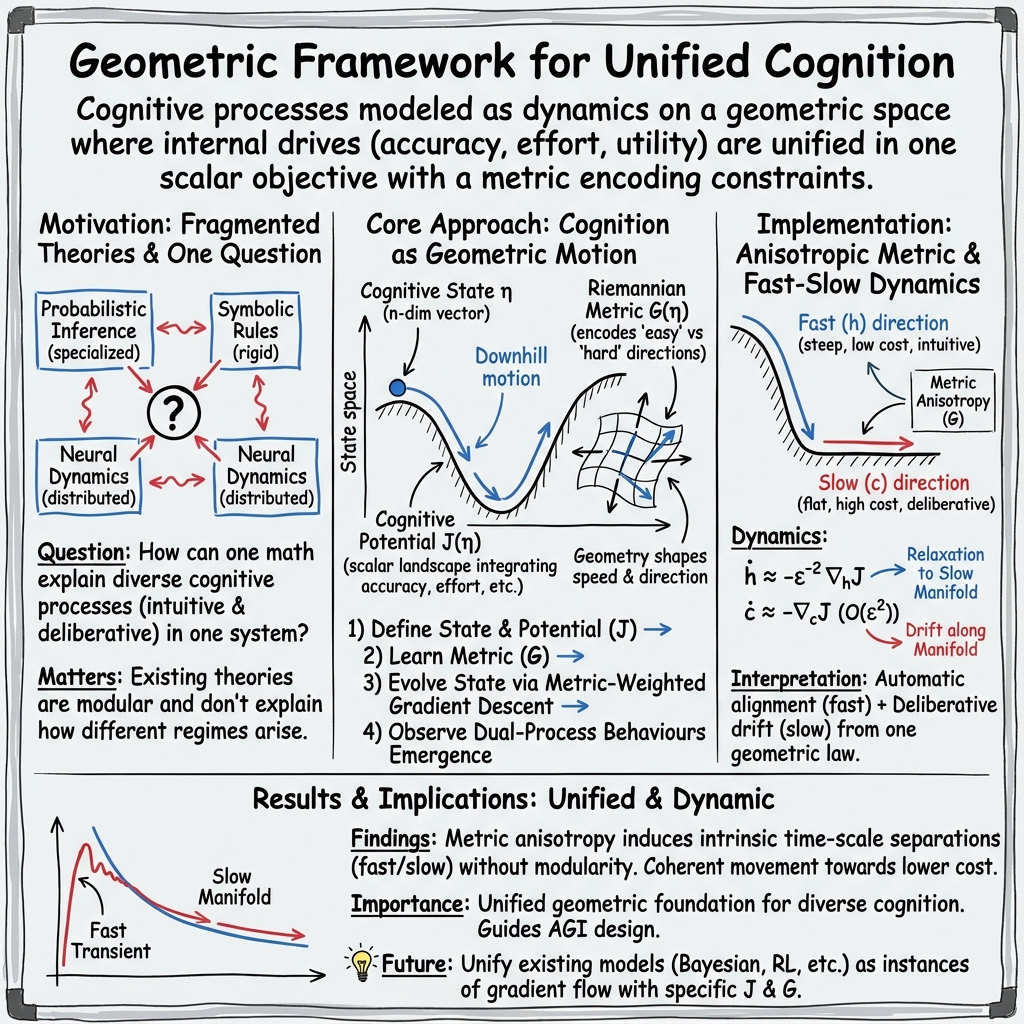
Abstract: Human cognition spans perception, memory, intuitive judgment, deliberative reasoning, action selection, and social inference, yet these capacities are often explained through distinct computational theories. Here we present a unified mathematical framework in which diverse cognitive processes emerge from a single geometric principle. We represent the cognitive state as a point on a differentiable manifold endowed with a learned Riemannian metric that encodes representational constraints, computational costs, and structural relations among cognitive variables. A scalar cognitive potential combines predictive accuracy, structural parsimony, task utility, and normative or logical requirements. Cognition unfolds as the Riemannian gradient flow of this potential, providing a universal dynamical law from which a broad range of psychological phenomena arise. Classical dual-process effects--rapid intuitive responses and slower deliberative reasoning--emerge naturally from metric-induced anisotropies that generate intrinsic time-scale separations and geometric phase transitions, without invoking modular or hybrid architectures. We derive analytical conditions for these regimes and demonstrate their behavioural signatures through simulations of canonical cognitive tasks. Together, these results establish a geometric foundation for cognition and suggest guiding principles for the development of more general and human-like artificial intelligence systems.

• The paper presents a mathematical framework that models cognitive states as points on a manifold using Riemannian gradient flow to minimize a scalar potential J.
• The paper employs a fast–slow decomposition, showing how an anisotropic metric produces dual-process dynamics with fast habitual and slow deliberative components.
• The paper validates the framework through simulations that confirm error scaling with the separation parameter and demonstrate stable manifold dynamics linked to cognitive phase transitions.

Geometric Unification of Cognitive Processes: An Expert Analysis of "A Geometric Theory of Cognition" (2512.12225)

Mathematical Formulation of Cognitive Dynamics

This work introduces a comprehensive geometric framework for cognition, formalizing the cognitive state as a point on a differentiable manifold endowed with a Riemannian metric $G(\eta)$. The internal state vector $\eta(t)$ evolves according to a gradient flow that minimizes a scalar cognitive potential $J(\eta)$, which encodes various behavioral and computational drives. The dynamical law is specified by

$$\dot{\eta}(t) = - G(\eta)^{-1} \nabla_\eta J(\eta),$$

with $J$ decomposable into terms reflecting prediction accuracy, complexity, reward, normative constraints, and effort. The Riemannian metric governs both the computational cost and feasible transitions in state space, allowing the model to naturally interpolate between cognitive architectures previously considered disparate.

Figure 1: The geometric framework models the cognitive state as a point on a manifold with a Riemannian metric, where cognition unfolds as gradient flow on a scalar potential.

Key to this formalism is that the gradient flow guarantees monotonic decrease of $J$ along trajectories, with fixed points corresponding to locally reconciled configurations—states with minimal prediction error, task conflict, or cost accretion. The metric structure enables anisotropic scaling of “effort” across cognitive directions, parameterizing which operations (e.g., perceptual updates vs. deliberative reasoning) are computationally favored.

Fast–Slow Decomposition and Dual-Process Emergence

A central claim substantiated both analytically and empirically is that anisotropy in the metric, specifically through a two-block structure with a scale separation parameter $\varepsilon$, gives rise to a canonical fast–slow dynamics:

$$G_\varepsilon = \begin{pmatrix} I_m & 0 \ 0 & \varepsilon^{-2} I_k \end{pmatrix}$$

This metric partitions the state space into (i) fast coordinates $h$ (e.g., habitual or perceptual variables) updated at $O(1)$ speed, and (ii) slow coordinates $c$ (e.g., deliberative, goal-directed components) evolving at $O(\varepsilon^2)$ speed:

$$\dot{h} = -\nabla_h J(h,c), \quad \dot{c} = -\varepsilon^2 \nabla_c J(h,c).$$

The paper rigorously proves (via geometric singular perturbation theory) the existence, when certain regularity and stability conditions on $J$ are met, of a slow manifold $\mathcal{M}_\varepsilon$ near which system trajectories remain. On $\mathcal{M}_\varepsilon$, the effective dimensionality is reduced, with the slow coordinate dynamics governed by the projected gradient of $J$ along $c$.

Figure 2: Numerical confirmation that anisotropic metrics induce timescale separation, with rapid collapse to a slow manifold followed by gradual evolution.

Figure 3: The stability of fast (automatic) variables and robustness to perturbation, ensuring rapid realignment to context-dependent equilibria.

Empirically, simulations demonstrate the rapid relaxation of $h$ to $h^*(c)$ and the subsequent slow drift of $c$. Observed error curves between the full system and reduced slow flow scale as $O(\varepsilon^2)$, precisely matching theoretical predictions.

Figure 4: Quantitative validation of reduced slow dynamics: the error between full and reduced trajectories decays with timescale separation parameter $\varepsilon$.

Figure 5: Visualization of energy landscape—trajectories fall into a valley (slow manifold) and evolve along it, aligning full system with reduced slow dynamics.

Behavioral Phenomena and Cognitive Phase Transitions

This framework exhibits dual-process cognitive regimes (intuitive vs. deliberative modes) not as the result of modular or hybrid system assumptions, but as a consequence of state-dependent geometry and potential landscape features. The model accounts for rapid intuitive responses through steep, energetically favorable directions and explains slower reasoning as drift along shallow, low-curvature regions. Furthermore, geometric phase transitions are observed where the slow variable $c$ undergoes abrupt switches as the potential landscape changes due to accumulated evidence or environmental change.

Figure 6: Simulated decision dynamics: fast automatic responses ($h$) rapidly align with habitual patterns while the slow variable ($c$) integrates evidence and eventually undergoes a discrete transition as the potential landscape reconfigures.

This unifying geometric approach reproduces hallmark behavioral signatures such as rapid habitual realignment, gradual evidence integration, and context-sensitive mode switching.

Theoretical and Practical Implications

The theoretical implications are multifold:

• Unification of Cognitive Theories: Bayesian inference, predictive coding, RL, deep latent models, GFlowNets, and dual-process frameworks are subsumed as special parametric instances of the geometric gradient-flow principle.
• Predictive Value: State- and curvature-dependent metrics systematically explain task difficulty, attentional load, resource allocation, and switching behavior without modular decomposition.
• Low-Dimensionality and Interpretability: The reduction to slow manifolds aligns with observed neural low-dimensionality and accounts for both transient and sustained cognitive phenomena.
• Architecture for AGI: The formulation suggests that artificial agents can be endowed with a latent state, global potential, and dynamically learned geometry, supporting adaptive allocation of computational resources and robust, multiscale reasoning—requirements critical for AGI.
• Stability: The use of Riemannian gradient flow endows systems with local and global stability properties, ensuring coherent and smooth behavioral evolution while allowing for sharp transitions when contextually appropriate.

Practically, this approach provides a blueprint for constructing agents whose cognition is not simply hierarchical or modular but emerges from the intrinsic geometry of representation space shaped during learning. Recent advances in world models, JEPA-style systems, and gradient-based planning architectures are mathematically encompassed within this geometric flow paradigm.

Future Directions

Several avenues for future exploration are indicated:

• Scalable Learning of Cognitive Potentials and Metrics: Data-driven (meta-)learning of both $J$ and $G$ in high-dimensional, multimodal environments.
• Integration with Neurobiological Data: Empirical validation of metric-induced timescale separation and manifold structure via neural population dynamics.
• Extension to Non-smooth or Discrete Manifolds: Accommodating symbolic or rule-based regimes within the geometric flow formalism.
• Design of Geometric AGI Systems: Implementation of artificial agents that learn and operate under state-dependent, manifold-constrained gradient flows.

Conclusion

This paper establishes a mathematically rigorous and empirically substantiated geometric framework that unifies diverse cognitive processes as gradient flow on a structured manifold. The approach elucidates the emergence of dual-process phenomena and demonstrates that timescale separation, low-dimensionality, and context-dependent cognitive switching are intrinsic consequences of learned representational geometry and potential landscapes. The implications for both theoretical cognitive science and the practical design of general intelligent systems are significant, suggesting a pathway toward robust, interpretable, and human-like artificial cognition.