JAX-in-Cell: A Differentiable Particle-in-Cell Code for Plasma Physics Applications (2512.12160v1)

Abstract: JAX-in-Cell is a fully electromagnetic, multispecies, and relativistic 1D3V Particle-in-Cell (PIC) framework implemented entirely in JAX. It provides a modern, Python-based alternative to traditional PIC frameworks. It leverages Just-In-Time compilation and automatic vectorization to achieve the performance of traditional compiled codes on CPUs, GPUs, and TPUs. The resulting framework bridges the gap between educational scripts and production codes, providing a testbed for differentiable physics and AI integration that enables end-to-end gradient-based optimization. The code solves the Vlasov-Maxwell system on a staggered Yee lattice with either periodic, reflective, or absorbing boundary conditions, allowing both an explicit Boris solver and an implicit Crank-Nicolson method via Picard iteration to ensure energy conservation. Here, we detail the numerical methods employed, validate against standard benchmarks, and showcase the use of its auto-differentiation capabilities.

• The paper introduces a novel, differentiable PIC framework built on JAX that integrates explicit and implicit solvers for plasma simulations.
• It validates the method against standard plasma benchmarks like Landau damping and two-stream instability, demonstrating high accuracy with energy and charge conservation.
• The work achieves significant GPU acceleration and enables gradient-based optimization, paving the way for scalable and flexible plasma physics research.

JAX-in-Cell: Differentiable Particle-in-Cell Simulation Framework in JAX

Introduction

JAX-in-Cell presents a fully electromagnetic, multispecies, and relativistic 1D3V Particle-in-Cell (PIC) framework implemented completely in JAX. The approach addresses limitations in both traditional high-performance PIC codes—often optimized for specific hardware and written in low-level languages—and educational Python scripts that cannot scale to modern plasma physics research requirements. Unlike production frameworks such as OSIRIS, EPOCH, VPIC, and WarpX, JAX-in-Cell achieves hardware-agnostic high performance, a unified implementation of explicit and implicit solvers, and the first native integration of automatic differentiation (AD) capabilities directly leveraging the JAX ecosystem. This enables scalable, rapidly prototypable, and gradient-based optimization workflows crucial for current applications in plasma physics, fusion, space, and laser-plasma science.

Numerical Structure and Implementation

JAX-in-Cell follows the standard PIC algorithmic paradigm: kinetic particles sample the Vlasov equation, with fields evolved via Maxwell's equations. Particles are advanced using both explicit and implicit time-stepping integrators. The explicit approach utilizes the Boris pusher, while the implicit method applies a Crank-Nicolson scheme solved via Picard iteration, ensuring discrete energy and charge conservation, especially relevant for long time-scale or stiff regimes.

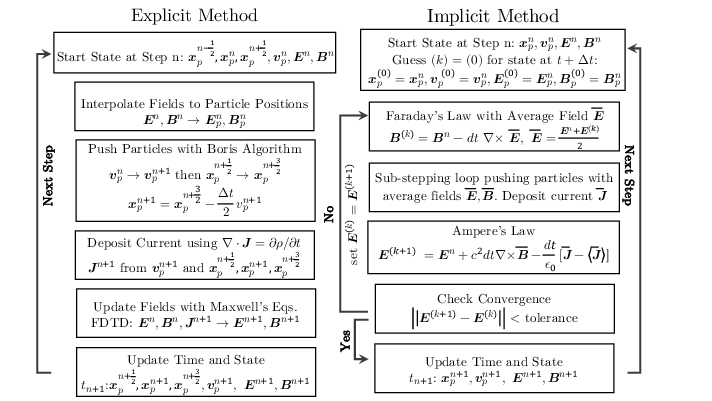
Figure 1: Schematic of explicit Boris and implicit Crank-Nicolson time-stepping algorithms in JAX-in-Cell, including field staggering on the Yee grid.

The codebase is modular, distributing tasks among six main modules for clarity and extensibility. The entire simulation state is managed as an immutable JAX tuple (carry), allowing seamless passage and functional composition—an architectural divergence from traditional object-oriented PIC implementations. Memory layout is monolithic with all particle species concatenated, optimized for vectorization and reducing GPU kernel launch overheads. All core numerical operations—charge deposition, field interpolation, field update, and particle push—are vectorized via jax.vmap and just-in-time compiled for backend performance parity.

Key features include:

• Yee lattice field discretization: Centered difference schemes with flexible (periodic, reflective, absorbing) boundary condition support.
• Charge-conserving current deposition: Discretely consistent with the continuity equation to preserve Gauss's law over arbitrary time evolution.
• High-order spline interpolation and digital filtering: Used in particle-to-grid operations to minimize aliasing and grid heating.
• Automatic differentiation: The entire PIC pipeline is AD-compliant, enabling gradients via both forward- and reverse-mode computation.

Validation and Benchmarking

Extensive validation is demonstrated via standard plasma instability benchmarks: Landau damping, two-stream instability, Weibel instability, and bump-on-tail instability. The benchmarks emphasize both the physical accuracy (comparison to analytic growth/damping rates) and algorithmic properties (e.g., energy conservation).

Figure 2: Time evolution of electric field energy demonstrates accurate linear growth/decay rates for Landau damping and two-stream instability, with quantitative agreement to analytic theory.

The Weibel instability test quantifies the magnetic field amplification and demonstrates the necessity of implicit energy-conserving integration for long simulations:

Figure 3: Temporal evolution of magnetic field energy and spatial magnetic field structure for Weibel instability, highlighting robust energy conservation with the implicit integrator.

The simulation of the bump-on-tail instability confirms accurate resolution of kinetic phase space structures and nonlinear wave–particle interactions:

Figure 4: PIC simulation resolves exponential growth phase and nonlinear phase-space evolution for bump-on-tail instability, capturing fine detail in the distribution function.

Performance Analysis

For computational performance, the code is benchmarked on both CPUs and modern GPUs. Performance scaling with respect to pseudo-particle count and hardware backend is empirically quantified. JAX-in-Cell achieves two orders of magnitude speedup on NVIDIA A100 hardware relative to CPUs, validating that high-level Python/JAX implementations can reach or exceed traditional PIC solver efficiency with appropriate vectorization and JIT compilation strategies. Floating-point precision impacts both fidelity and runtime, with 32-bit computation advantageous for large runs if physical tolerances permit.

Figure 5: Total runtime comparison and sampling error analysis as function of pseudo-particle number; GPU acceleration yields substantial reduction in computational time.

Differentiability and End-to-End Optimization

A key advance is the framework’s differentiability. JAX-in-Cell allows end-to-end gradient computation of macroscopic or diagnostic outputs with respect to underlying physical or algorithmic parameters. This is enabled without external adjoints or surrogate models. The paper demonstrates, as a canonical use case, gradient-based optimization of the two-stream instability growth rate with respect to the drift velocity parameter, using a damped Newton method powered by efficiently batched forward-mode JAX autodiff.

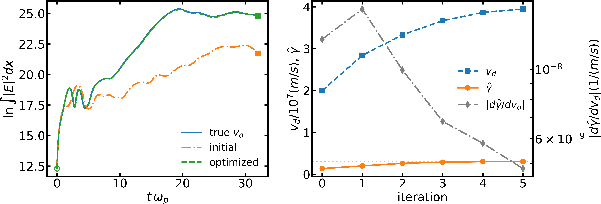
Figure 6: Autodifferentiation and optimization: drift velocity is iteratively optimized for a target growth rate for the two-stream instability, with rapid convergence demonstrated for both the objective value and sensitivity.

This capability is positioned as foundational for applications such as:

• Embedded PIC modules in differentiable simulators (e.g., Physics-Informed Neural Networks, PINNs).
• Inverse problems and Bayesian inference (parameter estimation from experimental data).
• Real-time control and optimal design (e.g., laser pulse shaping in plasma experiments).
• Gradient-based ML–physics code hybridization for surrogate modeling and uncertainty quantification.

The AD machinery is robust in the presence of vectorized GPU operations, but non-smooth numerical components may introduce challenges for gradient flow; the design mitigates these via extensive use of differentiable kernels and consistent vectorization.

Implications and Future Outlook

From a practical perspective, JAX-in-Cell enables high-fidelity kinetic plasma simulation workflows entirely in Python, accessible to the broader scientific and machine learning communities. By integrating the state-of-the-art AD capabilities from JAX, it facilitates direct optimization and embedding of physical models in hybrid AI pipelines. The theoretical impact is significant: it provides experimentalists and theorists with a flexible platform for rapid prototyping, automated discovery, and model-based data assimilation. These attributes are critical as data-driven methodologies become increasingly prevalent in fusion, astrophysics, and laser–plasma research.

JAX-in-Cell's differentiable design is expected to drive developments in:

• AI-accelerated methods for plasma diagnostics and control,
• End-to-end differentiable solvers for scientific machine learning,
• Automated testbeds for new implicit and high-order integrators,
• Integration of modern computational statistics for uncertainty-aware physical inference.

Conclusion

JAX-in-Cell demonstrates that high-performance, fully differentiable PIC simulations can be realized in Python leveraging JAX's vectorization and AD infrastructure. The framework establishes a new paradigm for plasma simulation—combining hardware efficiency, modular extensibility, and native differentiability—catalyzing AI integration and inverse modeling in kinetic plasma physics. Its validation against analytic benchmarks, performance on heterogeneous compute backends, and advanced optimization workflows collectively indicate substantial theoretical and practical impact. Future directions include broader support for higher-dimensional geometries, seamless ML code integration, and large-scale differentiable simulation suites for scientific discovery.

(2512.12160)