Kardar-Parisi-Zhang and glassy properties in 2D Anderson localization: eigenstates and wave packets (2512.12085v1)

Abstract: Despite decades of research, the universal nature of fluctuations in disordered quantum systems remains poorly understood. Here, we present extensive numerical evidence that fluctuations in two-dimensional (2D) Anderson localization belongs to the (1+1)-dimensional Kardar-Parisi-Zhang (KPZ) universality class. In turn, by adopting the KPZ framework, we gain fresh insight into the structure and phenomenology of Anderson localization itself. We analyze both localized eigenstates and time-evolved wave packets, demonstrating that the fluctuation of their logarithmic density follows the KPZ scaling. Moreover, we reveal that the internal structure of these eigenstates exhibits glassy features characteristic of the directed polymer problem, including the emergence of dominant paths together with pinning and avalanche behavior. Localization is not isotropic but organized along preferential branches of weaker confinement, corresponding to these dominant paths. For localized wave packets, we further demonstrate that their spatial profiles obey a stretched-exponential form consistent with the KPZ scaling, while remaining fully compatible with the single-parameter scaling (SPS) hypothesis, a cornerstone of Anderson localization theory. Altogether, our results establish a unified KPZ framework for describing fluctuations and microscopic organization in 2D Anderson localization, revealing the glassy nature of localized states and providing new understanding into the universal structure of disordered quantum systems.

• The paper provides conclusive numerical evidence that 2D Anderson localization fluctuations scale with a KPZ exponent (r^1/3) and follow Tracy-Widom GUE statistics.
• It maps eigenstate density fluctuations to rough interface growth and demonstrates directed polymer glassiness through dominant path pinning and avalanche phenomena.
• Wave packet analysis confirms single-parameter scaling with stretched exponential tails, unifying KPZ behavior with disorder-driven localization.

KPZ and Glassy Properties in 2D Anderson Localization: Eigenstates and Wave Packets

Introduction and Context

This paper presents conclusive numerical evidence that fluctuations in two-dimensional (2D) Anderson localization reside in the $(1+1)$-dimensional Kardar-Parisi-Zhang (KPZ) universality class, both at the level of localized eigenstates and time-evolved wave packets. The authors employ precise numerical diagonalization and efficient dynamical simulation techniques for the standard Anderson tight-binding model, focusing on regimes of strong disorder and large system sizes, to characterize both the fluctuation scaling and spatial organization of these quantum states.

The work positions itself against a longstanding challenge: while Anderson localization is analytically tractable in 1D, higher-dimensional cases lack a closed analytic description for fluctuations. This study delivers a unified KPZ framework for understanding the nature of disorder-induced fluctuations, extending from transport quantities to the internal structure of wavefunctions. A central element is the mapping between the quantum states and classical stochastic growth processes, notably the glassy directed polymer (DP) problem, which shares the same universality class.

Eigenstate Fluctuations and KPZ Scaling

The spatial profile and fluctuations of localized eigenstates are recast in terms of rough interface growth, identifying the logarithm of the eigenstate density with the interface height and radial distance as the KPZ growth "time." Figures illustrate the spatial density and this analogy:

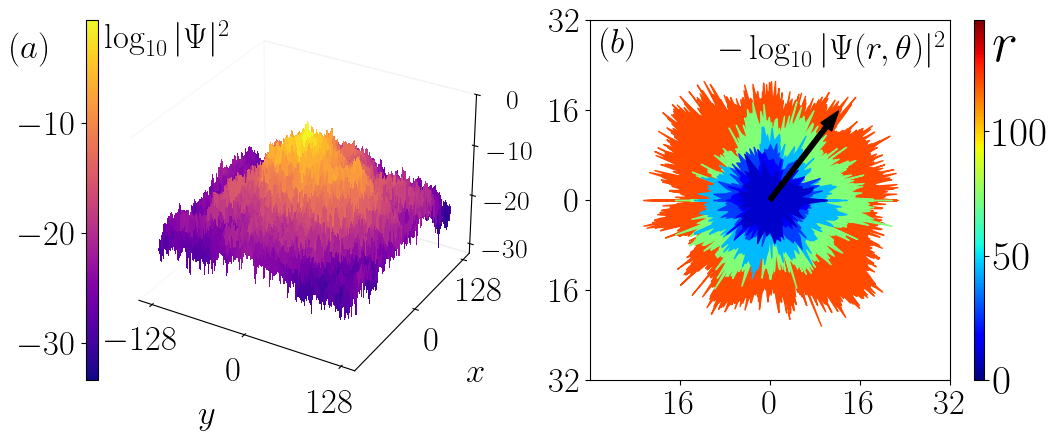
Figure 1: Logarithmic density of a localized eigenstate mapped onto a rough interface, with radial KPZ "time" parameter.

Spatial fluctuations of the logarithmic density, $\ln|\Psi(\mathbf{r})|^2$, grow with distance $r$ according to a KPZ scaling law, $\sigma(r) \sim r^{1/3}$, in contrast to the $\sim r^{1/2}$ law in 1D systems. The analysis utilizes both angular averaging (full circle at fixed radius) and fixed-direction sampling, consistently yielding the $(1+1)$ KPZ exponent.

Figure 2: Standard deviation of eigenstate logarithmic density displays $r^{1/3}$ scaling, confirming KPZ universality in 2D.

Crucially, the probability distribution of the rescaled logarithmic density converges to the Tracy-Widom (TW) form, specifically the GUE variant, for large $r$, manifesting the hallmark non-Gaussian, asymmetrical fluctuations expected in KPZ systems.

Figure 3: Probability distribution of rescaled density logarithm aligns with Tracy-Widom GUE, departing from Gaussian statistics for larger distances.

Directed Polymer Glassiness: Dominant Paths, Pinning, and Avalanches

Beyond the KPZ fluctuation scaling, the microscopic organization of eigenstates exposes strong glassy features analogous to the directed polymer problem. For a fixed realization of disorder, the dominant contribution to the wave amplitude at a remote observation point originates from a single optimal path (or branch), selected by the random landscape. The sensitivity of the eigenstate to local perturbations (response function) reveals sharply localized paths, confirming this DP-like picture.

Figure 4: Response function maps identify sharp dominant paths connecting the localization center to observation points, mirroring directed polymer configurations.

The behavior of these dominant paths as the observation direction varies exhibits characteristic pinning (stable plateau regions) and avalanche (abrupt jumps) phenomena:

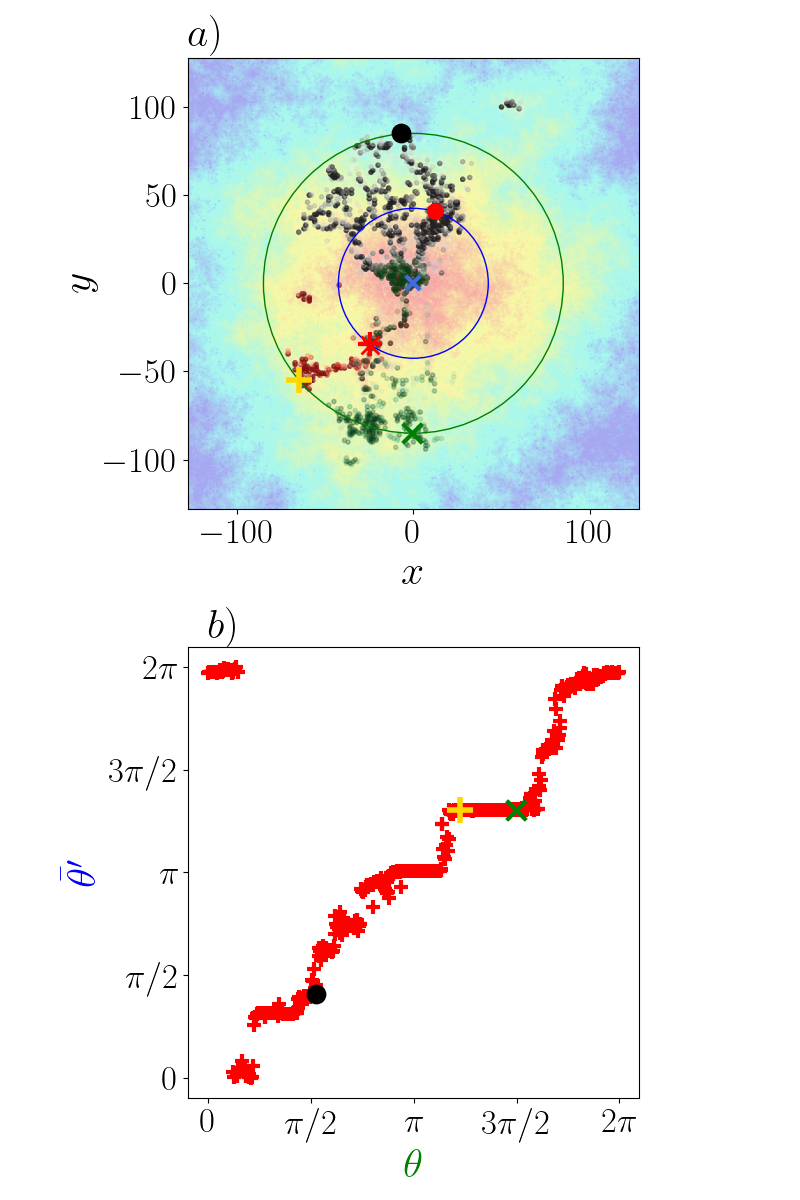
Figure 5: Average angular position of a dominant path remains pinned as the observation point’s angle varies, with sudden jumps indicating avalanches.

Scaling analysis shows the transverse wandering of the dominant path at midway grows as $r^{2/3}$, matching the DP wandering exponent, and rescaling data collapses plateau and jump structure across different path lengths:

Figure 6: Arc length scaling for pinning and avalanche regions collapses after rescaling by KPZ/DP correlation length.

Figure 7: Path midpoint variance follows $r^{2/3}$ scaling, corroborating the directed polymer analogy.

Wave Packet Fluctuations, Stretched Exponential Tails, and SPS Validity

Long-time evolved wave packets reveal that their spatial profiles (density envelopes), for both point and line initial conditions, are exponential in their mean but possess rare large fluctuations following the KPZ scaling law. The standard deviation of the logarithmic density again exhibits the $r^{1/3}$ exponent, and the density profile fits a stretched exponential form predicted by KPZ theory. Both the typical and average density profiles collapse onto universal curves when plotted against rescaled distance $r/\xi$, affirming single-parameter scaling (SPS).

Figure 8: Mean-square displacement of wave packets saturates, signaling localization and readiness for precise profile measurement.

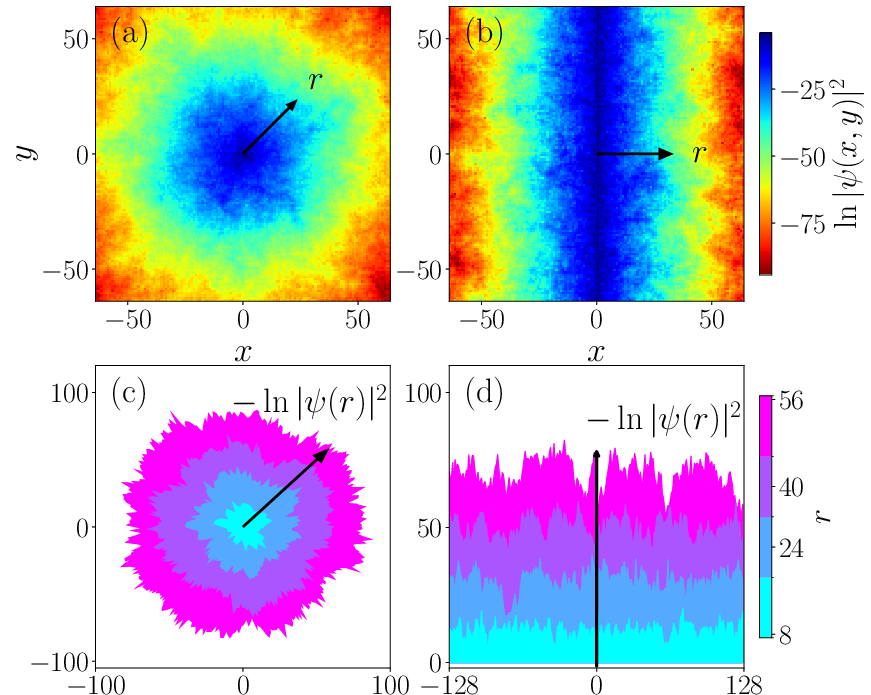
Figure 9: Spatial representation of wave packet density mapped as rough KPZ interfaces: point and line initial conditions.

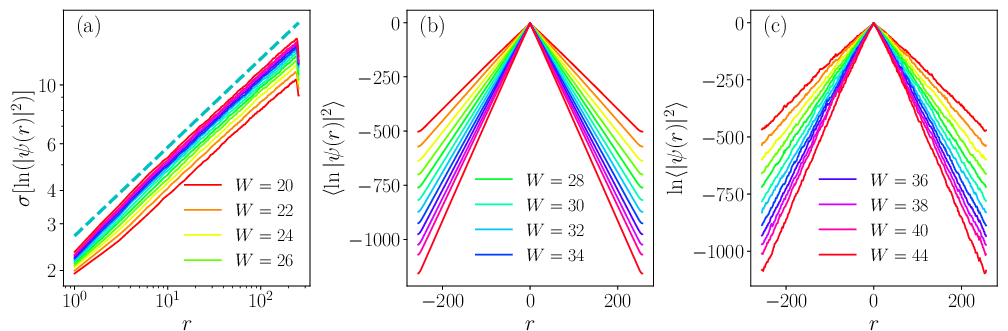
Figure 10: Standard deviation and profiles for wave packet logarithmic density match KPZ scaling and show universal collapse across disorder strengths.

The localization length $\xi$ conforms to an exponential law as a function of inverse disorder strength, in line with theoretical expectations for 2D Anderson localization:

Figure 11: Logarithm of localization length as a function of inverse disorder strength fits the expected 2D scaling law.

Further, the derivative of the typical density with respect to distance reveals stretched-exponential corrections characteristic of KPZ fluctuations:

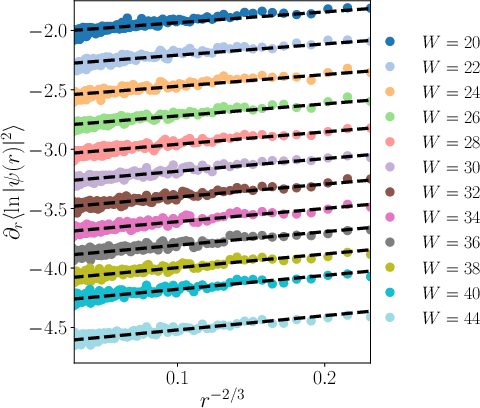
Figure 12: Characteristic $r^{-2/3}$ correction in the derivative of the log-density confirms stretched exponential behavior.

The universal collapse of both average and typical wave densities across disorder strengths when expressed with rescaled coordinates demonstrates that KPZ-type fluctuation corrections coexist with SPS:

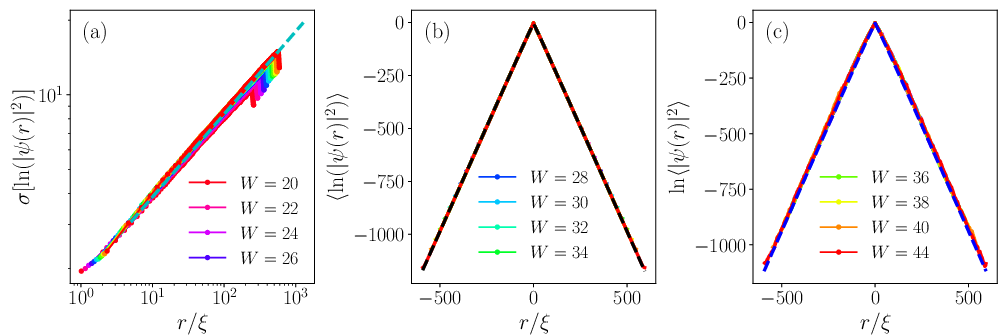
Figure 13: Universal collapse of density fluctuations, typical, and average density profiles when rescaled by localization length, spanning disorder strengths.

Broader Implications and Future Directions

The findings unify the description of fluctuation phenomena in 2D Anderson localized systems, providing a direct and quantitative bridge to classical KPZ and glassy DP theories. This serves to clarify microscopic mechanisms behind rare-event statistics and anisotropic localization, beyond standard transport properties.

Practically, the results imply that strong-disorder quantum systems will exhibit KPZ-like, non-Gaussian tails in observables (e.g., matter-wave or optical profiles), and that wavefunction organization is highly anisotropic and controlled by glassy, path-dependent mechanisms. The confirmed compatibility between KPZ scaling and SPS further validates the single-parameter scaling hypothesis even in the presence of broad fluctuation corrections, maintaining predictive power for disorder-induced localization.

Extensions to higher dimensions, random graph topologies, many-body localized systems, and periodically driven (Floquet) systems suggest fertile ground for future study, where generalizations of KPZ and glassy physics may organize extreme-value statistics and spatial structure.

Conclusion

This work rigorously establishes that the universal fluctuations and microscopic structure in 2D Anderson localization are governed by KPZ and directed polymer universality. Both static and dynamic properties—localized eigenstates and evolved wave packets—exhibit KPZ scaling, stretched-exponential tails, and glassy phenomena (pinning and avalanches of dominant paths). The results confirm while extending theoretical expectations, demonstrating the coexistence of KPZ fluctuations alongside single-parameter scaling. This advances the fundamental understanding of disordered quantum systems at strong localization and sets the stage for further investigation into rare-event statistics, higher-dimensional effects, and interacting systems.