The reversed "von Karman/Brazier effect" and a compendiary analytical solution (2512.11528v1)

Abstract: The goal of the present study is to offer some accurate analytical formulae for the evaluation of the here defined reversed "von Karman/Brazier's effect", which may appear at first sight anomalous and has previously been noticed and successively explained using both Finite Element analyses and approximate analytical formulations. The proposed analytical formulae, based on the previous contribution of one of the present authors and on the Donnell's equations for cylindrical shells can be helpful in emphasizing the possible impact that some arrangements may have in various fields and especially in offshore engineering and can assist design calculations.

• The paper introduces a comprehensive analytical solution using Donnell’s shell theory and Fourier decomposition to characterize the reversed von Kármán/Brazier effect.
• Key results show that restraining ovalisation leads to compressive stresses exceeding tensile ones, with findings validated through experiments and FE simulations.
• The model enables rapid design-stage evaluation for offshore pipelines with stiffeners, offering practical insights for limit state design and structural reliability.

Analytical Characterization of the Reversed von Kármán/Brazier Effect in Cylindrical Shells

Introduction

This paper addresses the reversed "von Kármán/Brazier effect" in cylindrical shells subjected to bending, providing a compendiary analytical solution rooted in Donnell’s shell theory. The phenomenon of cross-sectional ovalisation during bending of thin-walled cylindrical shells, originally modeled by von Kármán and later extended by Brazier, is fundamental in the structural response of pipes, especially in offshore engineering contexts. The introduction of stiffeners or buckle arrestors inhibits this ovalisation, leading to significant alterations in the strain and stress distributions. The paper's analytical formulations enable rapid evaluation of such effects, circumventing the need for computationally expensive finite element models.

Figure 1: Buckle arrestors.

Experimental Basis and Phenomenological Description

The von Kármán/Brazier effect documents the cross-sectional deformation (ovalisation) arising during bending loads on cylindrical shells. In traditional test setups, such as the four-point bending rig (Figure 2), the expectation under classical flexure theory is symmetric tensile and compressive axial strains under pure bending.

Figure 2: Typical four-point bending test arrangement.

However, experimental campaigns on instrumented pipes with reinforced collars (preventing local ovalisation) revealed a persistent deviation: compressive strains exceeded tensile ones—contrary to theoretical predictions. Conversely, when local ovalisation was permitted, tensile strains could dominate. These results expose a critical impact of the boundary and constraint conditions on the shell's response; these findings are corroborated with full-field FE simulations.

Analytical Formalism—Imposed vs. Restrained Ovalisation

The paper develops analytical expressions describing stress and strain states under both imposed and restrained ovalisation. Utilizing Donnell's equations for thin cylindrical shells and the beam-on-elastic-foundation analogy, the ovalising pressure and deformation fields are constructed.

When an ovalisation is imposed (e.g., via inward-directed forces at mid-span—see Figure 3), the stress distribution departs from the canonical symmetric form; maximum tensile strains become larger than compressive ones. The analytical approach decomposes the loading into a Fourier series of circumferential modes and characterizes the resulting radial displacement, strain, and stress through closed-form expressions.

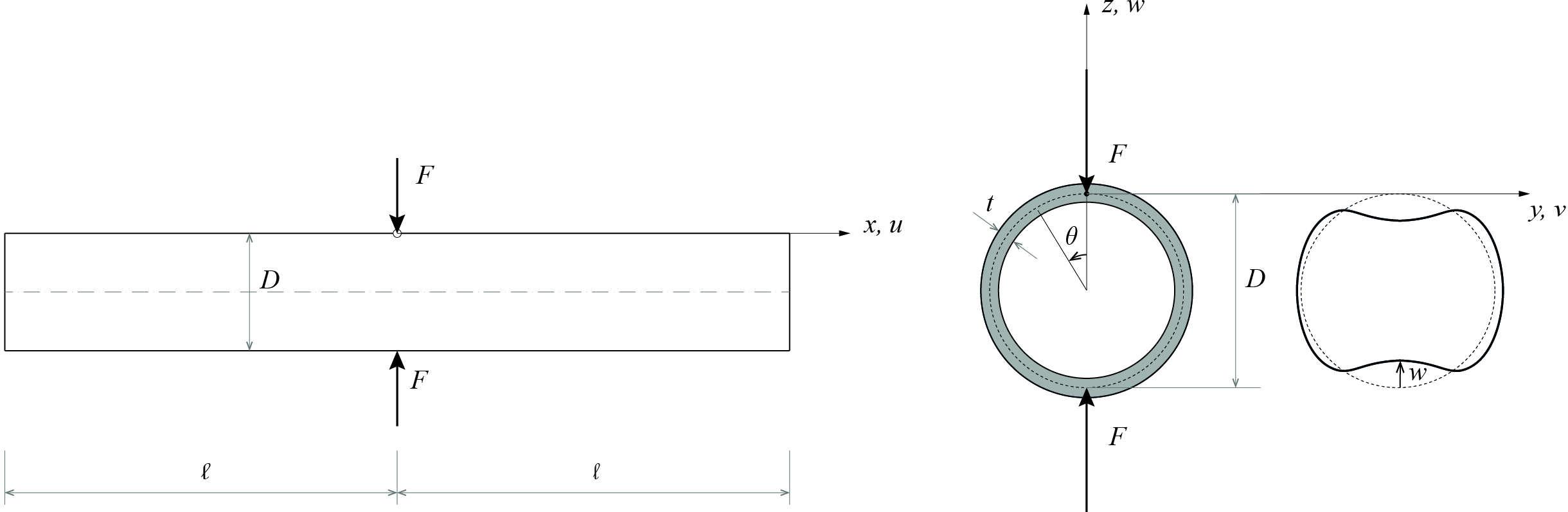
Figure 3: Circular cylindrical shell loaded by two opposite inward forces at the half-length section: coordinate system and notations.

In the case of long-wave dominated deformation ($D/t$ typical of offshore pipelines), the longitudinal response can be effectively modeled by a 1D beam on elastic foundation (Figure 4). Analytical treatment yields explicit relationships for displacements and foundation stiffness, capturing essential physical mechanisms.

Figure 4: Beam-on-elastic foundation analogy.

For restrained ovalisation—the "reversed von Kármán/Brazier effect"—the presence of circumferential stiffeners or boundary features enforces an alternative stress state. Here, the pressure that would typically drive ovalisation is resisted, resulting in a counteracting force (as in the superposition framework shown in Figure 5). The analytical solution predicts that compressive strains/stresses at the pipe wall become greater than their tensile counterparts.

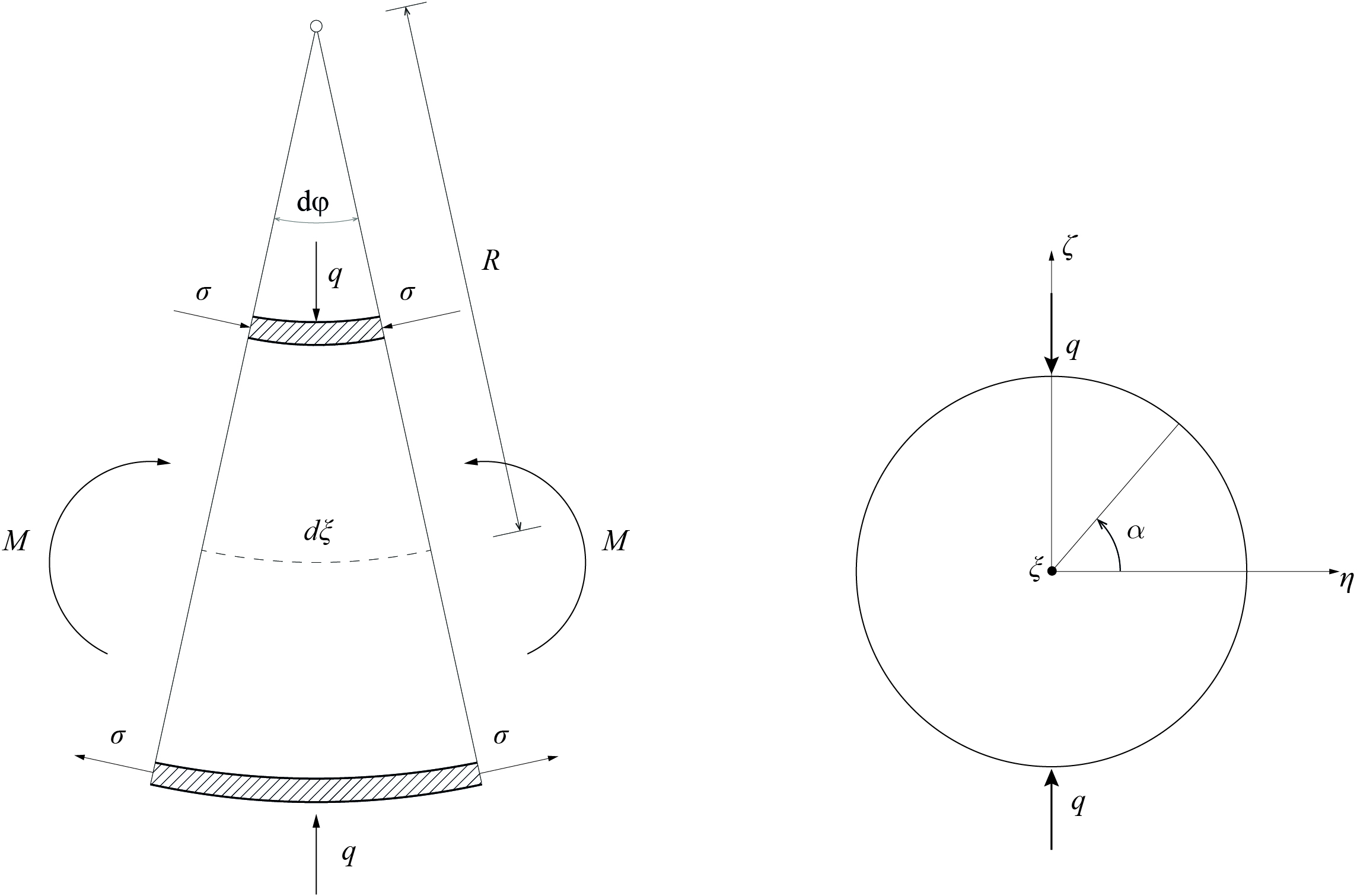
Figure 5: Axial stresses and resulting ovalising pressure.

Validation with Experimental and Numerical Data

Quantitative validation is performed using experimental data from tests on steel pipes ($E=208$ GPa, $\nu=0.3$, $D=608.6$ mm, $t=18.9$ mm), combined with FE analyses. The analytical solution accurately captures the measured asymmetry in top and bottom longitudinal strains under both imposed and restrained ovalisation (Figure 6), matching the observed strain distributions with errors in the 10–15% range.

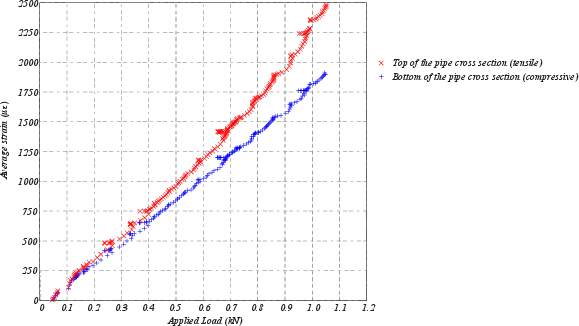
Figure 6: Averaged strain along the top and bottom of the pipe bend test specimen (bottom strain reported with reversed sign).

The imposed ovalisation setup is further detailed, with explicit comparison of theoretical and experimental strain profiles (Figure 7) and force-induced displacement/strain fields along the pipe axis (Figure 8). For a specific applied force (27,478.5 N), the magnitude and profile of the vertical displacement and longitudinal strain are quantitatively reproduced by the analytical model, with FE results (Ansys) providing independent confirmation.

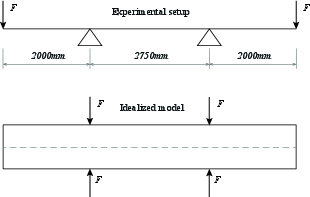
Figure 7: Experimental setup: the case of imposed ovalisation.

Figure 8: Vertical displacement (top) and Longitudinal strain (bottom) of the points at at the top of the cross section along the axis of the cylindrical shell for a force of 27,478.5N applied at $x=0$.

Finally, the longitudinal stress field measured 1.8 m from the ovalisation-prevented section is shown to agree with analytical predictions (Figure 9), validating the superpositional arguments.

Figure 9: Longitudinal stress at the section located 1.8 m from the section with ovalisation prevented.

Implications and Future Directions

The compact analytical formulations facilitate rapid, design-stage assessment of stress redistributions in cylindrical shells where ovalisation is controlled by local or distributed stiffening (e.g., buckle arrestors in offshore pipelines). This has clear implications for limit state design, local buckling curvature estimation, and reliability assessment in critical infrastructure. The robust agreement with both experiments and FE models reinforces the method’s suitability as a design and verification tool in scenarios where rapid iteration is requisite or simulation resources are constrained.

Pragmatically, the model can be extended to the analysis of dynamic events, non-axisymmetric loading, or thermomechanical coupling in advanced materials. Theoretically, the results highlight the centrality of constraint-induced stress redistribution in thin-walled shell instability, prompting further exploration of analogous effects in anisotropic or composite shells, as well as shells with more complex boundary conditions.

Conclusion

This study formalizes the reversed von Kármán/Brazier effect in cylindrical shells by deriving and validating analytical solutions for stress and deformation states under both imposed and prevented ovalisation. The framework provides quantitative predictions in strong agreement with experimental measurements and numerical simulations, offering practical utility for the design and assessment of pipelines and shell structures where ovalisation constraints are present. The results motivate further work to encompass a broader class of shell and boundary scenarios, with direct applicability to structural engineering and beyond.