Distributionally Robust Regret Optimal Control Under Moment-Based Ambiguity Sets (2512.10906v1)

Abstract: In this paper, we consider a class of finite-horizon, linear-quadratic stochastic control problems, where the probability distribution governing the noise process is unknown but assumed to belong to an ambiguity set consisting of all distributions whose mean and covariance lie within norm balls centered at given nominal values. To address the distributional ambiguity, we explore the design of causal affine control policies to minimize the worst-case expected regret over all distributions in the given ambiguity set. The resulting minimax optimal control problem is shown to admit an equivalent reformulation as a tractable convex program that corresponds to a regularized version of the nominal linear-quadratic stochastic control problem. While this convex program can be recast as a semidefinite program, semidefinite programs are typically solved using primal-dual interior point methods that scale poorly with the problem size in practice. To address this limitation, we propose a scalable dual projected subgradient method to compute optimal controllers to an arbitrary accuracy. Numerical experiments are presented to benchmark the proposed method against state-of-the-art data-driven and distributionally robust control design approaches.

• The paper presents a tractable convex reformulation of the regret-optimal control problem using moment-based ambiguity sets.
• It develops a dual projected subgradient algorithm that scales efficiently to high-dimensional systems compared to standard SDP solvers.
• Numerical experiments show that the proposed controllers balance robustness and conservatism better than traditional methods.

Distributionally Robust Regret Optimal Control Under Moment-Based Ambiguity Sets

Problem Motivation and Context

Traditional stochastic control assumes precise knowledge of stochastic disturbance distributions, which in practice are subject to misspecification, sample error, and non-stationarity. To mitigate degradation in performance from model mismatch, distributionally robust control (DRC) optimizes for worst-case performance with respect to a prescribed ambiguity set of plausible disturbance distributions. However, DRC methods often yield overly conservative controllers, which may lead to suboptimal empirical performance when the true distribution is less adversarial.

To address the tradeoff between robustness and conservatism, recent work has proposed regret-optimal control, formulating the controller design as the minimization of the worst-case expected regret—the expected excess cost compared to an omniscient, noncausal controller (oracle) with full knowledge of the disturbance realization. This paper generalizes previous regret-optimal control frameworks by constructing ambiguity sets based on moment uncertainty, where the mean and covariance of the disturbance are only known to reside in norm-balls (including Schatten norms), thus capturing a broad class of distributions, including non-Gaussian and temporally correlated processes.

Formulation and Theoretical Results

The paper studies finite-horizon, discrete-time, linear time-varying (LTV) systems driven by additive disturbances with unknown joint distributions. The system states and disturbances may be temporally dependent and arbitrarily distributed, subject only to their first two moments lying within Euclidean (mean) and Schatten norm (covariance) balls around nominal values.

Controllers are restricted to the class of strictly causal affine disturbance feedback policies, ensuring convexity properties required for tractable optimization. The regret for a policy $\phi$ and disturbance $w$ is $R(\phi(w), w) = J(\phi(w), w) - J(o(w), w)$, where $J$ is a quadratic cost and $o$ is the noncausal oracle. The control objective is thus

$$\inf_{\phi} \sup_{P \in \mathcal{P}} \mathbb{E}_P[R(\phi(w), w)]$$

where $\mathcal{P}$ is the moment-based ambiguity set.

The expected regret of any affine $\phi$ depends only on the disturbance mean and covariance, so the worst-case expected regret splits into separate maximizations over those quantities. The ambiguity set is defined as: $$\mathcal{P} : = \{ P ~|~ \|\mu - \bar{\mu}\|_2^2 \le r_1,~ \|\Sigma - \bar{\Sigma}\|_p \le r_2\}$$ where $p$ is the Schatten norm order, and dual norm $q$ (with $1/p + 1/q = 1$) appears in the controller synthesis via regularization.

Main theoretical results:

• The paper gives a tractable convex reformulation of the minimax control synthesis as a regularized linear-quadratic stochastic control problem, where the regularization simultaneously accounts for mean and covariance ambiguity via spectral- and Schatten-norm terms, interpolating between standard robust and nominal stochastic LQG design.
• The optimal feedback controller has a structure that decomposes into a feedforward term equivalent to the expected action of the oracle (under the nominal mean), and a feedback term calibrating to deviations from the nominal mean.
• The convex program can be equivalently expressed as an SDP, making it expressive but, for large horizons or system dimensions, computationally costly.

Scalable Solution Methods

While the SDP-based reformulation is general, interior point solvers scale poorly with problem dimension and horizon. The authors develop a dual projected subgradient algorithm operating over the dual regularization parameters (related to mean and covariance uncertainty), with primal updates as convex quadratic programs and projection steps over Schatten norm balls for the covariance. The dual function remains concave with non-empty subdifferentials, and, under positive definiteness, the algorithm reduces to projected gradient ascent, allowing fast convergence and consideration of large-scale problems.

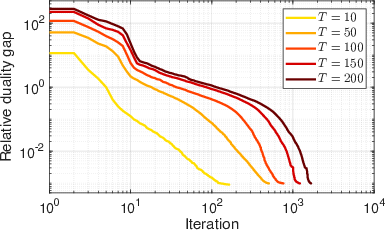
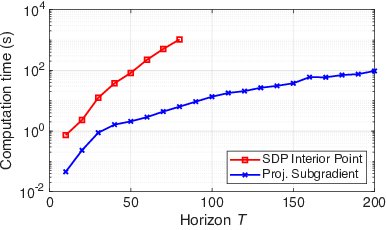
Figure 1: Relative duality gap versus iteration count and computational runtime comparing the dual projected subgradient method with a generic SDP solver.

Numerical Results

Numerical experiments evaluate the proposed controllers (with Schatten norm ambiguity) against state-of-the-art methods, including those based on Wasserstein ambiguity sets, sample average approximation (SAA), and an oracle with perfect model knowledge. The disturbance process is an AR(1) process, with the correlation parameter $\rho$ sweeping from independent to highly correlated settings.

Key findings:

• All robust controllers outperform SAA at moderate ambiguity radii, but excessive penalization leads to over-conservatism; selecting ambiguity radii is thus critical, but can be achieved in practice through cross-validation.
• At optimal radii, for temporally uncorrelated disturbances ($\rho=0$), the Spec-Regret controller achieves out-of-sample performance indistinguishable from the oracle.
• As $\rho$ increases, Wass-Cost delivers minimal expected cost only in a narrow high-correlation regime, while the proposed regret-minimizing formulations (especially Spec-Regret and Frob-Regret) deliver consistently superior ex-ante regret across all disturbance correlations, avoiding over-conservatism.

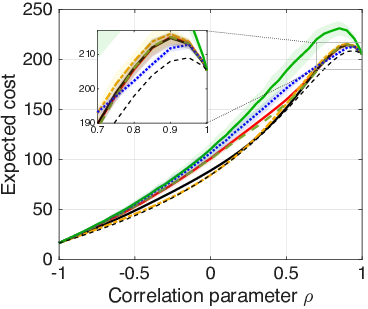
Figure 2: (a) Expected cost versus ambiguity set radius at $\rho=0$, (b) expected cost, and (c) ex-ante regret versus disturbance autocorrelation for each controller at their optimal ambiguity radii.

Practical and Theoretical Implications

The framework successfully interpolates between robust, nominal, and mean/covariance-driven uncertainty paradigms by tuning the ambiguity set parameters $(r_1, r_2, p)$. When $r_1 \to 0$ and $r_2 \to 0$, nominal SAA/LQG design is recovered; when $r_1 \to \infty$, robust design emerges; as $r_2 \to \infty$ and $p = \infty$, the controller reduces to the classic LQR. Schatten norm selection enables tailored robustness to different types of covariance uncertainty; e.g., spectral norm penalizes worst-case variance, nuclear norm yields isotropic penalties.

On the computational side, the projected subgradient method provides an efficient, scalable solver for large finite-horizon problems, enabling deployment in high-dimensional control tasks and longer horizons than generic SDP solvers. Empirically, the gap between practical runtime for the dual method and traditional SDP solvers widens rapidly as problem size increases.

Future Directions

Further avenues include extensions to infinite-horizon settings, partially observed systems, and adaptive estimation of ambiguity set parameters from data with guarantees. Another area is integration with distributional uncertainty quantification methods (e.g., via empirical likelihood or other moment-constrained distributional models), and exploration of additional forms of regularization or ambiguity interpolation (such as Wasserstein or $\phi$-divergence sets) beyond moment-based frameworks.

Conclusion

This paper establishes a rigorous paradigm for synthesizing finite-horizon, distributionally robust regret-optimal controllers under moment-based ambiguity, characterized by tractable convex reformulation and scalable dual optimization methods. Compared to state-of-the-art distributionally robust and regret-centric control methods, the proposed framework achieves strong out-of-sample cost and regret performance, particularly in the presence of limited data and distributional uncertainty, with significant implications for data-driven robust control in practical settings.

Reference: "Distributionally Robust Regret Optimal Control Under Moment-Based Ambiguity Sets" (2512.10906)