Extrapolation of Periodic Functions Using Binary Encoding of Continuous Numerical Values (2512.10817v1)

Abstract: We report the discovery that binary encoding allows neural networks to extrapolate periodic functions beyond their training bounds. We introduce Normalized Base-2 Encoding (NB2E) as a method for encoding continuous numerical values and demonstrate that, using this input encoding, vanilla multi-layer perceptrons (MLP) successfully extrapolate diverse periodic signals without prior knowledge of their functional form. Internal activation analysis reveals that NB2E induces bit-phase representations, enabling MLPs to learn and extrapolate signal structure independently of position.

• The paper introduces NB2E, a binary representation that converts continuous values into bit vectors, allowing MLPs to extrapolate periodic signals accurately.
• The paper demonstrates that NB2E leverages bit-phase interactions to enable position-independent learning, outperforming Fourier and continuous input strategies.
• The paper shows robust empirical performance across simple and composite periodic signals, emphasizing NB2E's potential for function regression and sequence modeling.

Extrapolation of Periodic Functions Using Binary Encoding of Continuous Numerical Values

Introduction

This work introduces and systematically evaluates Normalized Base-2 Encoding (NB2E), a novel binary representation for continuous numerical inputs, demonstrating that NB2E enables vanilla MLPs to extrapolate periodic functions far beyond the training domain. The key contribution is the demonstration that, when input as base-2 binary vectors, vanilla MLPs learn internal representations—specifically, bit-phase interactions—that allow for position-independent learning of periodic structures without resorting to explicit functional priors or architectural changes.

Binary Encoding for Continuous Values

NB2E encodes a scalar input $x \in [0,1)$ as a binary vector $\gamma(x) = [B_1, B_2, \ldots, B_N]$, where $x = \sum_{i=1}^{N} B_i 2^{-i}$ with each $B_i \in \{0,1\}$. The choice of $N$ provides a precision-sample trade-off: the paper finds $N=48$ is generally sufficient. All input values are normalized to $[0,1)$ before encoding.

Figure 1: 48-element NB2E encoding of 0.987654321, showcasing the binary vector structure that forms the input for the network.

Critically, effective training with NB2E requires that each bit position in the vector be exposed to both 0 and 1 within the train set; thus, the train set must span up to at least 0.5 after normalization to ensure activation of all high-order bits.

Architecture and Baselines

The study employs deep MLPs with five dense layers (512 units each, ELU or sine activations, $L_2$ regularization $\lambda=10^{-4}$). Three input schemes are compared: NB2E, Fixed Fourier Encoding (FFE)—which encodes scalar input as sine/cosine pairs for exponentially increasing frequencies, and standard continuous scalar input.

Figure 2: MLP architecture diagram; NB2E replaces the continuous input, mapping the normalized value into a binary vector.

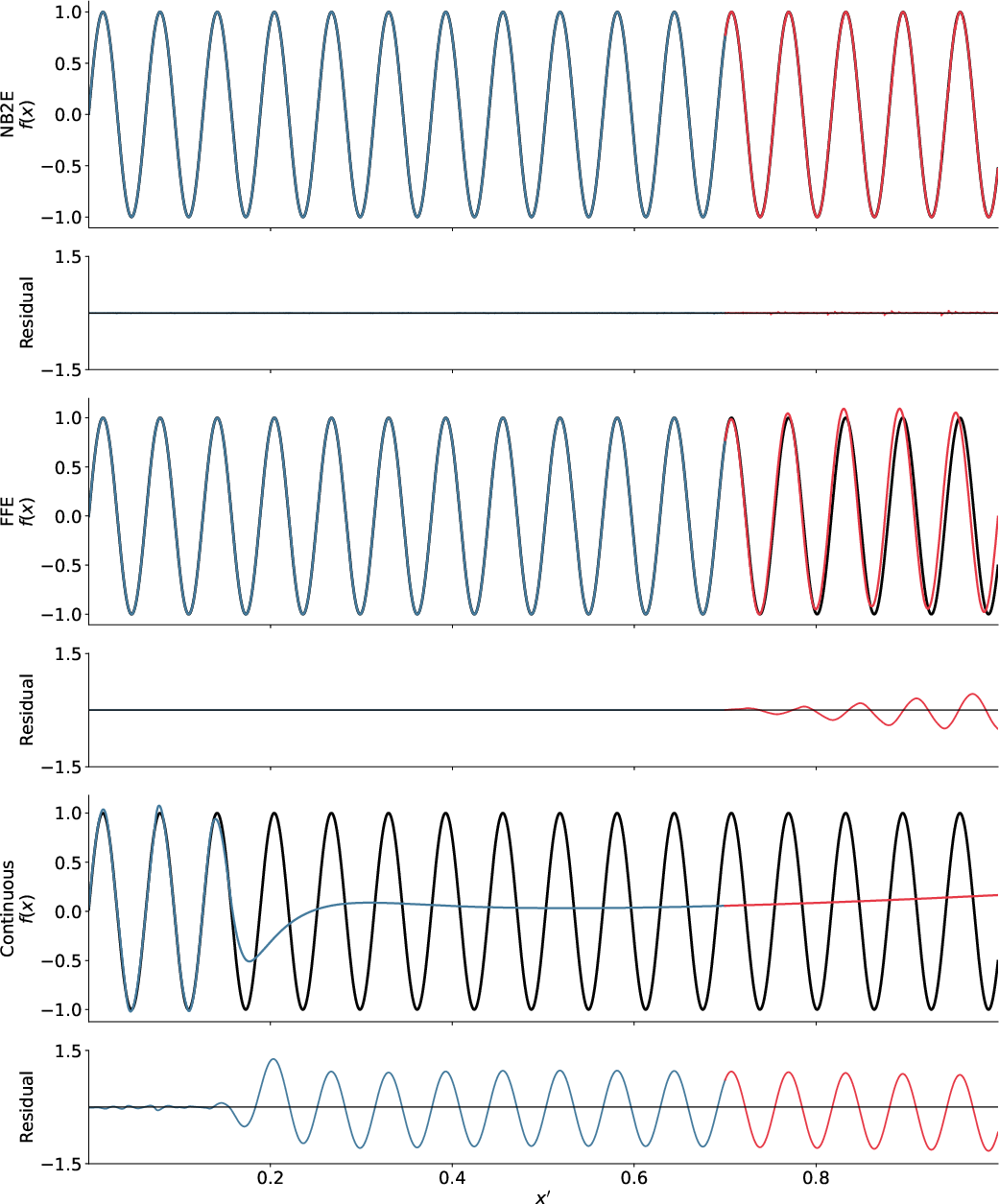
Empirical Results: Extrapolation and Signal Complexity

The study evaluates the capacity for periodic extrapolation on a range of tasks, from simple sines to nontrivial periodic composites (sine sum, sawtooth/triangle combinations, and mixtures including exponential and stepwise features).

• On simple sinewaves, MLPs with NB2E input extrapolate with negligible error well beyond their training interval.

  Figure 3: Accuracy of NB2E, FFE, and continuous input MLPs on sine function extrapolation; only NB2E retains fidelity in the extrapolation regime.

• For composite or nonsinusoidal periodic signals, NB2E-equipped MLPs continue to extrapolate with fidelity unattainable by FFE or continuous inputs, whose predictions collapse to noise or diverge rapidly outside the training bound.

Sensitivity Analyses

Training Domain Coverage

The study rigorously tests sensitivity to the maximum input value seen during training. If the train domain does not reach $x' \geq 0.5$, catastrophic phase discontinuities occur where the corresponding bits flip for the first time, validating the hypothesis that all bits must be sampled for proper generalization.

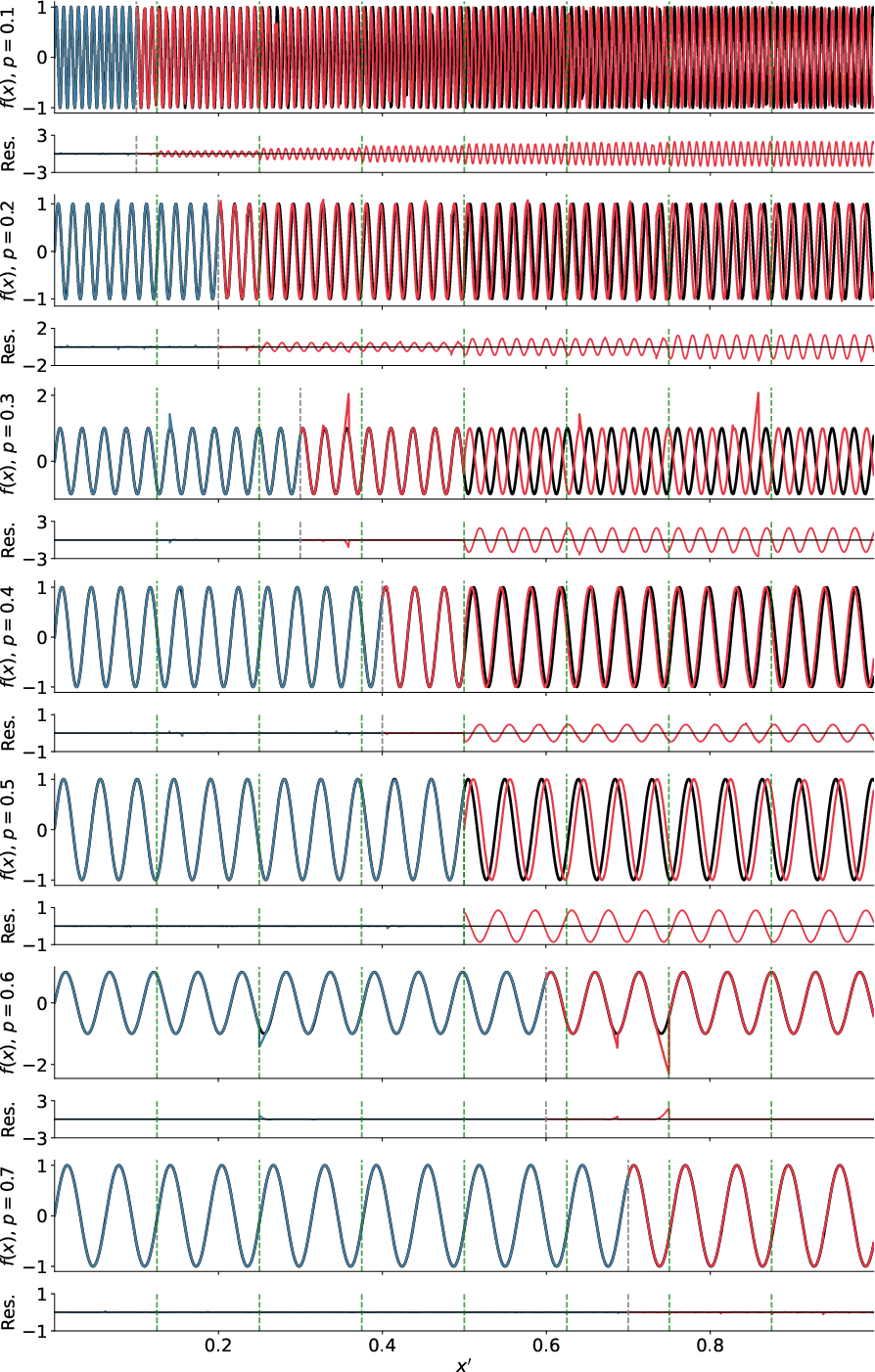
Figure 4: Extrapolation error as a function of train/test split locations, demonstrating bit-boundary failure if NB2E input bits are untrained.

Data Density and Noise Robustness

Even with as few as 250 points, NB2E MLPs learn to extrapolate a sinewave, with performance monotonically improving as training set size increases. The addition of Gaussian noise to the output moderately degrades extrapolation but does not destroy the periodic structure inferred via NB2E.

Figure 5: Effect of increasing output noise on NB2E MLP extrapolation; the fundamental periodicity remains detectable well outside the train region.

Internal Representations: Bit-Phase Decomposition

A critical part of the analysis interrogates the latent representations learned by the network. UMAP projections of the hidden-layer activations reveal that the network organizes samples not by input position $x$ but by phase in the periodic signal, mapped through interactions of specific NB2E bit combinations.

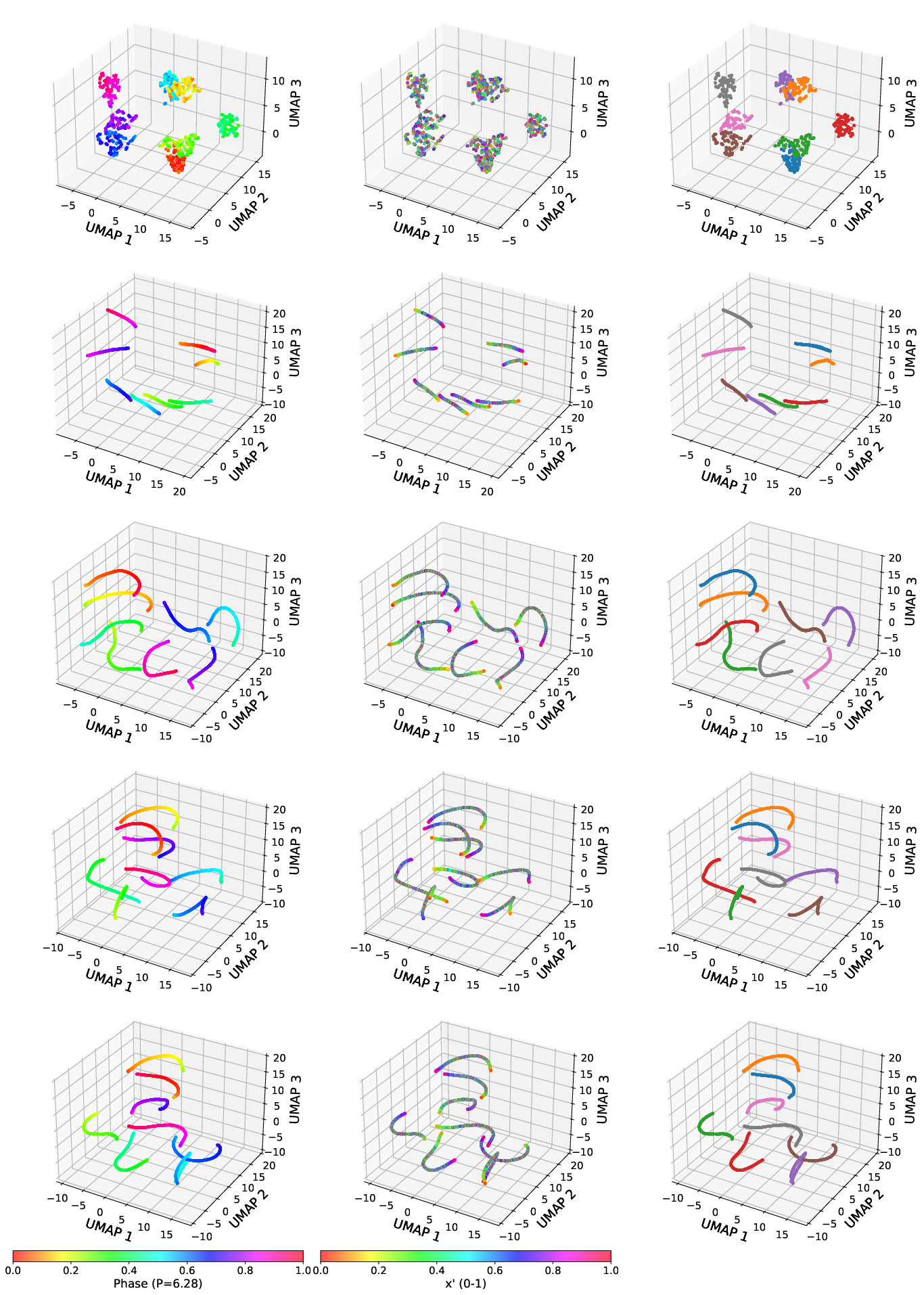
Figure 6: UMAP projection of MLP activations, colored by signal phase, position, and cluster ID; bit-phase grouping is evident at all hidden layers.

This partitioning generalizes: for composite signals, the MLP constructs internal representations corresponding to several independent phase coordinates, encoded jointly with bit patterns.

Figure 7: UMAP projections for composite periodic inputs; different columns encode respective phase relations of individual constituent signals.

Enhancement with Periodic Activations

Replacing ELU with sine activations further improves the quality of extrapolation, especially on more complex signals. The NB2E+sinusoidal-activation pairing is empirically superior for precise periodic extrapolation.

Figure 8: Residual comparison between ELU and sine activations in MLPs fed with NB2E input vectors.

Theoretical and Practical Implications

• Encoding Inductive Bias: NB2E's bitwise decomposition acts as a learned multi-resolution step-function basis; this supports the hypothesis that neural networks extrapolate periodicity more effectively when the input encoding explicitly enumerates all positional transitions.
• Separation from Frequency Domain Encodings: Despite sharing the same set of frequency scales as FFE, only NB2E enables position-independent phase learning and extrapolation, indicating that the discrete (rather than continuous) structure of the input basis is vital.
• Scalability: The NB2E method generalizes to any continuous coordinate, offering a compelling alternative to time- or position-based input features that require both precision and extrapolative capacity.
• Task Limitations: The method requires explicit normalization to ensure all bits are trained. Extrapolation is limited to the next power-of-two boundary, though this is adjustable by normalization.

Future Directions

Open theoretical questions remain concerning the precise role of discrete bit transitions in inductive bias for function extrapolation and the formal mathematical justification for why only binary encodings support this regime. Using NB2E in higher dimensions and within more complex architectures (e.g., sequence models, transformers, PINNs) is also an attractive domain for future work.

Conclusion

The introduction of NB2E unlocks position-agnostic extrapolation of periodic signals in vanilla MLPs, outperforming both Fourier encodings and direct numerical inputs in accuracy and generality. By transforming the input into a hierarchical bit-phase space, MLPs develop representations that support stable, accurate signal extension into unobserved domains, providing a robust new tool for function regression and sequence modeling where periodic or cyclical structure is present (2512.10817).