Gradient projection method and stochastic search for some optimal control models with spin chains. II (2512.10290v1)

Abstract: This article (II) continues the research described in Morzhin O.V. Gradient projection method and stochastic search for some optimal control models with spin chains. I (submitted), derives the needed finite-dimensional gradients corresponding to the infinite-dimensional gradients obtained in Article I, both for transfer and keeping problems at a certain $N$-dimensional spin chain, and correspondingly adapts a projection-type condition for optimality, gradient projection method (GPM). For the case $N=3$, the given in this article examples together with Example 3 in Article I show that: a) the adapted GPM and genetic algorithm (GA) successfully solved numerically the considered transfer and keeping problems; b) the two- and three-step GPM forms significantly surpass the one-step GPM. Moreover, GA and a special class of controls were successfully used in such the transfer problem that $N=20$ and the final time is not assigned.

• The paper presents finite-dimensional gradients that enable efficient projection-based optimization for state transfer and stabilization in quantum spin chains.
• It introduces multi-step gradient projection variants with Polyak momentum acceleration, reducing computational cost by up to 21× for N=3 spin chains.
• Stochastic methods such as genetic algorithms scale effectively to high-dimensional problems (N=20), achieving robust optimization under realistic noise conditions.

Gradient Projection Method and Stochastic Search for Optimal Control of Spin Chains

Problem Setting and Formulation

This work presents an in-depth treatment of quantum optimal control (QOC) models with finite-length spin chains, focusing on state transfer and stabilization objectives. The system dynamics are specified by $N$-level time-dependent Schrödinger equations with control-affine Hamiltonians, where the controls enter both linearly and nonlinearly. The study considers both the traditional transfer problem (state-to-state transition in fixed time) and a "keeping" problem (stabilization/maintenance) under general pointwise amplitude constraints for controls. Piecewise constant parameterizations of controls are used for discretization, enabling practical computation.

A key contribution is the derivation of finite-dimensional gradients corresponding to the infinite-dimensional gradients obtained previously for these quantum optimal control problems. The adjoint equations and their specific structure for transfer and keeping objectives are formulated, allowing explicit and efficiently computable gradient expressions under the discretization scheme. These results underpin adaptations of the gradient projection method (GPM) to the quantum setting, with specialized constraint handling for admissible control sets.

Numerical Optimization Methods and Algorithmic Advances

The study rigorously develops and implements first-order (GPM-1S), second-order (GPM-2S), and third-order (GPM-3S) forms of the gradient projection method, integrating momentum-inspired Polyak terms for acceleration. The projection step respects box constraints on the control amplitudes, ensuring admissibility in each iteration.

Strong empirical evidence is provided that GPM-2S and GPM-3S offer substantial reductions in computational cost (by factors of up to 21× compared with GPM-1S) for transfer and stabilization tasks on $N=3$ spin chains (Figure 1).

Figure 1: GPM-2S achieves excitation transfer, with convergence and infidelity evolution displayed for all GPM forms on $N=3$ chains; final population is concentrated at the target site.

Genetic algorithms (GA), leveraging a parameterized trigonometric form for controls, are also employed as a stochastic baselines. For both transfer and keeping objectives, GAs achieve comparably low infidelities with significantly fewer solved time-evolution problems than naive GPM-1S schemes (Figure 2).

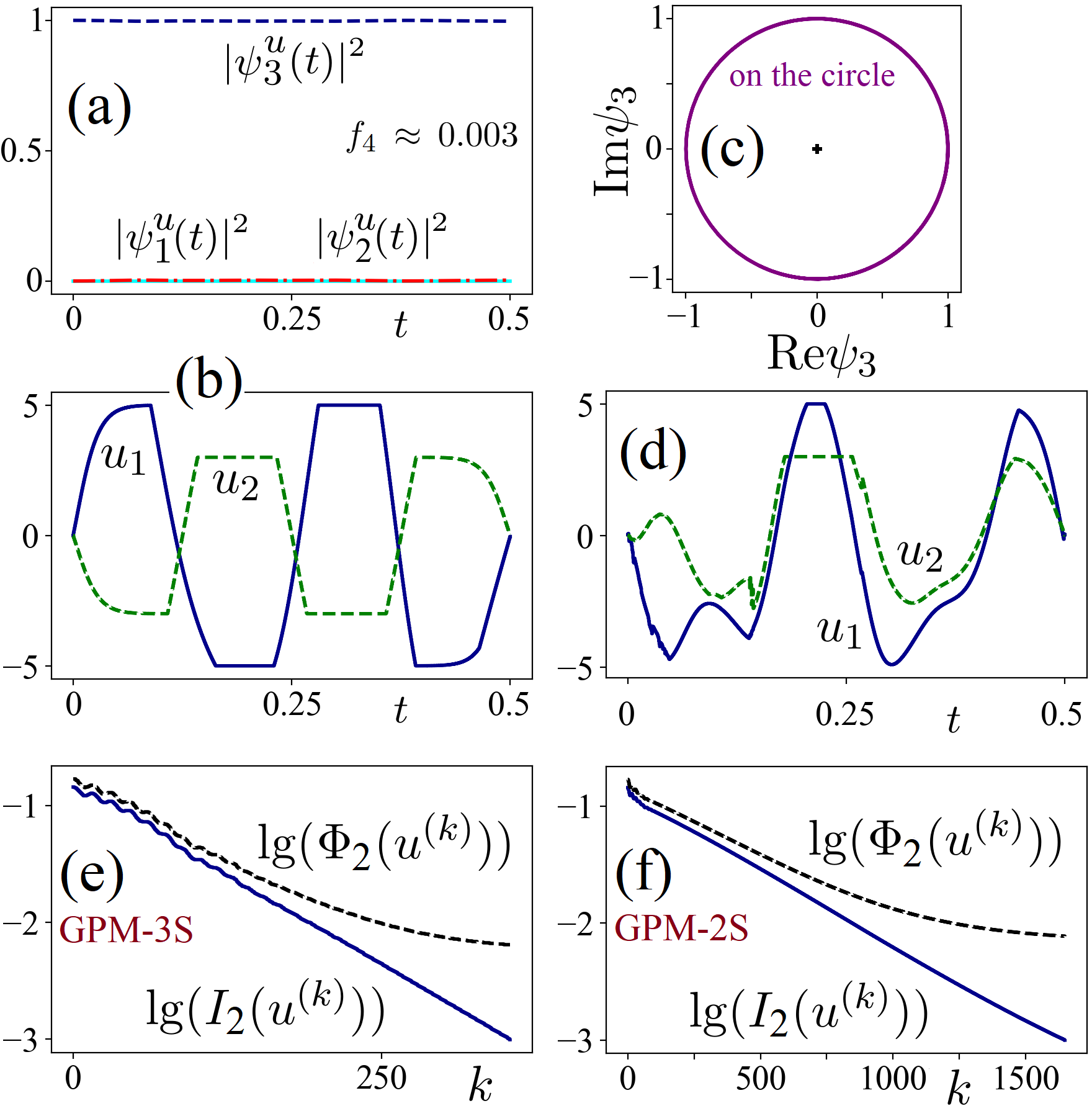
Figure 2: GA-optimized controls nearly preserve the ground state over the time interval (keeping), while GPM-3S and GPM-2S exhibit rapid convergence compared to GPM-1S.

For large chains ($N=20$), state transfer without allocated terminal time is reformulated as a joint optimization in both controls and transfer duration. GAs achieve infidelity below $1\%$ in these high-dimensional problems, showing scalability of the stochastic approach (Figure 3).

Figure 3: For $N=20$, GA yields near-complete transfer within the optimized time window; individual site populations and control profiles are illustrated.

Robustness Analysis and Theoretical Insights

Comprehensive Monte Carlo robustness tests are conducted by injecting i.i.d. Gaussian noise into the GA-optimized controls for the $N=20$ chain. Statistically, even with moderate noise ($\sigma=0.05$ to $0.2$), the final transfer infidelity median increases marginally from $0.014$ to $0.093$ (see Table 3 of the paper), indicating substantial resilience of the designed controls in the face of implementation imperfections.

Theoretically, the finite-dimensional gradients lead to a projection-type first-order optimality condition over the control space, without any global convexity or strong convexity assumptions. The GPM-2S and GPM-3S variants, inspired by Polyak's heavy-ball method, empirically and theoretically mitigate stagnation at non-optimal stationary points, as the momentum terms help to escape shallow suboptimal basins—a property relevant for quantum control landscapes, which are often highly nonconvex.

Furthermore, the presented methodology is flexible regarding the enforcement of amplitude constraints—often omitted in the quantum control literature. The difference in convergence between GPM variants is attributed to the exploitation of historical gradient and iterate information, which is particularly advantageous in high-dimensional, stiff optimization problems.

Implications and Future Research Directions

The results demonstrate that higher-order GPM variants and stochastic search heuristics can efficiently solve challenging QOC problems with practical control constraints. For small spin chains ($N=3$), GPM-3S consistently achieves high-precision results with orders-of-magnitude fewer quantum system evolutions than GPM-1S, which is critical for offline pulse design and real-time applications. For larger systems ($N=20$), the success of GAs in joint control-amplitude and time optimization confirms the expressiveness of the parametrized control sets and the method's scalability.

In practice, the robustness to control noise suggests that designed pulses may be directly transferable to experimental setups, especially in quantum communication and transport applications utilizing spin-chain architectures. From a theoretical perspective, the methodology offers a framework to compare local (gradient-based) and global (stochastic) search strategies on identical quantum control problems under constraints, providing a testbed for future algorithmic innovations.

Potential directions include: adaptive selection of GPM step and momentum parameters, hybridization with global search metaheuristics, and extension to open-system dynamics (Lindblad-type dissipation). Additionally, exploring connections to landscape topology, such as analyzing the frequency and nature of local traps for the different GPM variants, provides an avenue for connecting optimal control theory with quantum information processing.

Conclusion

By constructing finite-dimensional projected gradient algorithms and benchmarking them against genetic heuristics on prototypical quantum state transfer and stabilization tasks, this study advances the theory and practice of constrained quantum optimal control. Key findings highlight the superior efficiency of multi-step GPM, the viability of stochastic search for high-dimensional chains, and significant noise robustness, collectively opening new opportunities for control synthesis in quantum-technological platforms such as quantum communication channels and spintronic devices.