Photonic Quantum-Accelerated Machine Learning (2512.08318v1)

Abstract: Machine learning is widely applied in modern society, but has yet to capitalise on the unique benefits offered by quantum resources. Boson sampling -- a quantum-interference based sampling protocol -- is a resource that is classically hard to simulate and can be implemented on current quantum hardware. Here, we present a quantum accelerator for classical machine learning, using boson sampling to provide a high-dimensional quantum fingerprint for reservoir computing. We show robust performance improvements under various conditions: imperfect photon sources down to complete distinguishability; scenarios with severe class imbalances, classifying both handwritten digits and biomedical images; and sparse data, maintaining model accuracy with twenty times less training data. Crucially, we demonstrate the acceleration and scalability of our scheme on a photonic quantum processing unit, providing the first experimental validation that boson-sampling-enhanced learning delivers real performance gains on actual quantum hardware.

• The paper presents a hybrid Quantum Optical Reservoir Computing framework using boson sampling to achieve up to 20x data efficiency in ML tasks.
• It deploys fixed photonic reservoirs on integrated hardware, demonstrating superior performance on MNIST and biomedical datasets amid class imbalances.
• The study validates high experimental fidelity between simulations and photonic QPU outputs, emphasizing the impact of quantum coherence in ML acceleration.

Photonic Quantum-Accelerated Machine Learning via Boson Sampling

Introduction and Background

The intersection of quantum physics and ML promises computational advantages by leveraging the complexity and capacity of quantum systems. The paper "Photonic Quantum-Accelerated Machine Learning" (2512.08318) presents an explicit experimental and theoretical framework for accelerating classical ML classification tasks using boson sampling as a quantum resource. Boson sampling, a restricted model of non-universal quantum computation with demonstration of quantum computational advantage in photonic hardware [Arute et al. 2019; Zhong et al. 2020], is classically intractable due to its output sampling complexity scaling as $N^N$ (with $N$ the photon number). This work operationalizes boson sampling as the reservoir for a quantum-classical hybrid scheme—Quantum Optical Reservoir Computing (QORC)—and systematically evaluates both numerical and hardware realizations.

QORC Architecture

QORC implements reservoir computing, where a fixed, unoptimized nonlinear system (the reservoir) expands classical input features into a high-dimensional space, with only the readout layer being trainable. In QORC, the reservoir is a boson sampling device realized on an integrated photonic chip with Fock-state photon inputs and single-photon detectors. Dataset features, reduced via principal component analysis (PCA), are encoded into phases of the quantum circuit between two random interferometric networks (pre-circuit and reservoir). The multimode output is sampled, standardized, and fed to a linear classifier. Notably, no quantum circuit backpropagation or parameter updates are performed—the quantum resource is static, minimizing hardware control requirements.

Figure 1: Workflow of the QORC scheme, highlighting the mapping of PCA-reduced features onto quantum optical phases for boson sampling, followed by linear classification.

Empirical Performance: Classical Tasks with Quantum Acceleration

MNIST Classification and Data Efficiency

Benchmarking on the MNIST classification task, the QORC classifier significantly outperforms a classical linear support vector classifier (L-SVC) in both accuracy and data-efficiency. Specifically, QORC achieves up to a 4.9% absolute improvement in test accuracy depending on the reservoir size, and notably, retains model performance with as little as 1/20 the training data required by a classical classifier. Saturation of test accuracy occurs at only $\sim2500$ training images with QORC, compared to the $60,000$ required for L-SVC with classical features, facilitating large reductions in classical data labeling and computational cost.

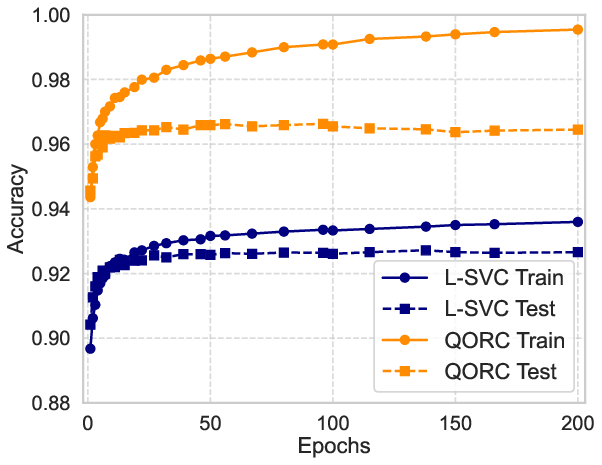
Figure 2: MNIST classification accuracy as a function of training epochs, demonstrating QORC’s consistent outperformance over L-SVC even from the first epoch.

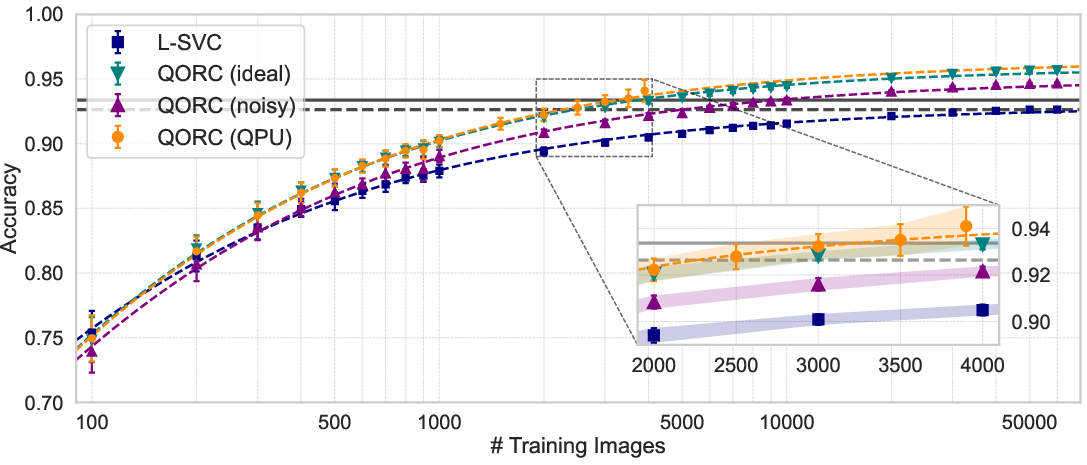
Figure 3: Quantitative relationship between MNIST test accuracy and training set size, with QORC maintaining high accuracy at extreme data sparsity—validating quantum data-efficiency claims.

Reservoir Size, Indistinguishability, and Quantum Advantage

Model accuracy monotonically grows with the Hilbert space dimensionality, determined by photon number $N$ and mode number $M$. The distinction between contributions from quantum first-order versus second-order coherence is experimentally probed via photon indistinguishability sweeps. Even with completely distinguishable photons, QORC delivers advantage over classical, emphasizing the value of quantum coherence over entanglement alone in reservoir-based classification tasks.

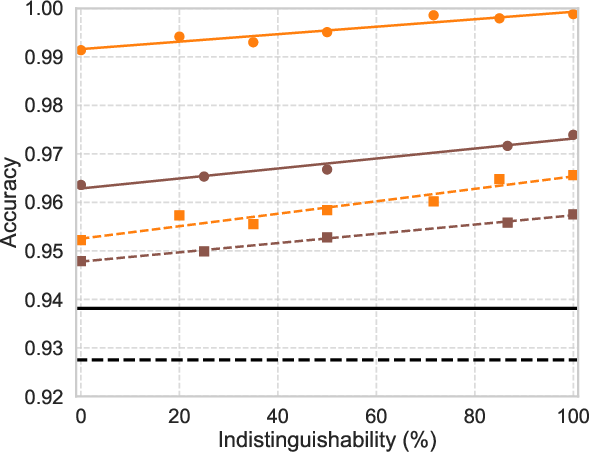
Figure 4: Dependence of QORC classification accuracy on single-photon indistinguishability, establishing robust quantum advantage regardless of input photon coherence.

Imbalanced and Biomedical Datasets

The architecture’s resilience is further tested on the MedMNISTv2 biomedical suite and artificially imbalanced MNIST variants, where QORC systematically outperforms classical baselines in macro F1 score (a more reliable metric under label imbalance). Performance increases are maintained for real-world clinical images with severe class imbalance and low SNR, signaling applicability beyond synthetic balanced benchmarks.

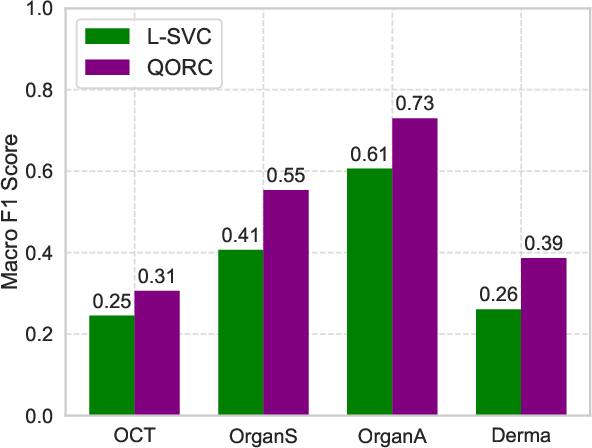
Figure 5: Macro F1 score improvements on diverse MedMNISTv2 biomedical datasets, highlighting QORC performance under real-world data imbalances.

Hardware Implementation on Photonic Quantum Processing Units

The paper is unique in validating its quantum acceleration claims on physical integrated photonic hardware: testing was performed on Quandela's Ascella cloud QPU, using 3-photon inputs over 12 modes. High statistical overlap between numerical simulations and experimental samples was measured (TVD $\sim0.1$; KS $\sim0.07$), confirming faithful physical realization of reservoir distributions and thus reliability of predictions obtained from quantum hardware.

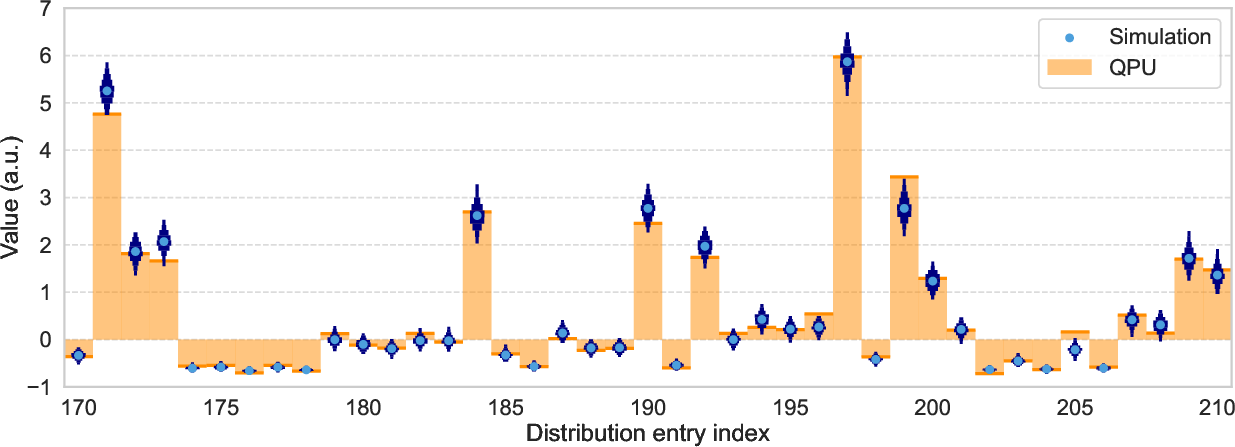
Figure 6: Statistical comparison between simulated and QPU-acquired boson sampling distributions, illustrating experimental fidelity for single MNIST sample embeddings.

Comparison with Neural Architectures

QORC’s empirical advantage diminishes with more expressive classical neural network architectures but remains significant compared to shallow and linear models. For deep neural architectures, the utility of random quantum reservoirs depends on the relative informativeness of quantum features versus increased input sparsity/noise—a trade-off that can be mitigated by selective feature engineering or increased sampling depth.

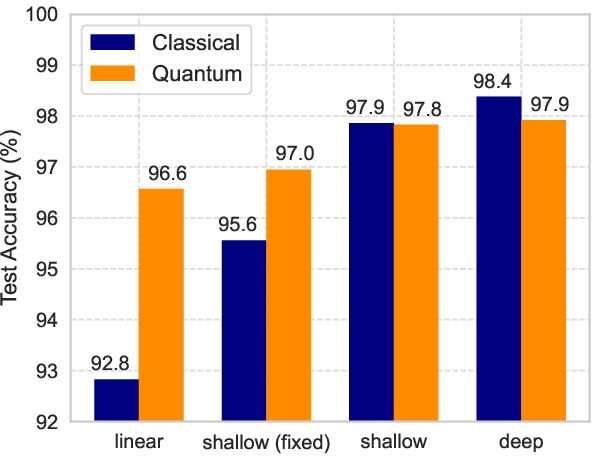
Figure 7: Classification accuracy versus network depth/architecture for MNIST, demonstrating progressive reduction of quantum reservoir impact as model expressivity grows.

Implications and Outlook

QORC provides experimental evidence that static photonic quantum systems can be harnessed for genuine ML acceleration on real, not hypothetical, quantum hardware. The system achieves target test accuracies with up to 20x less classical data, substantiating claims of quantum data-efficiency advantage. This data-sparsity tolerance translates to cost savings in data collection/labeling, broadens applicability to resource-constrained domains, and reduces the environmental footprint of ML training.

Looking towards hardware scalability, the authors note the impending exponential increase in integrated photonic fidelity, efficiency, and clock rates, predicting orders-of-magnitude improvements that will enable ultra-high dimensionality quantum reservoirs.

From a theoretical perspective, the work supports the practical utility of intermediate quantum models (boson sampling, GBS) as reservoirs for nonlinear, high-dimensional expansions in ML, without demanding universal quantum computation. The approach is immediately extensible to time-series/temporal tasks, nonlinear function fitting, and dynamical systems forecasting.

Conclusion

"Photonic Quantum-Accelerated Machine Learning" (2512.08318) offers a comprehensive demonstration—both in simulation and on photonic QPU hardware—of the tangible benefits of quantum reservoir architectures for ML. The QORC scheme is robust to imperfections, tolerant to device noise, and delivers measurable acceleration in terms of reduced data requirements and improved imbalanced-data performance. As photonic platforms mature, quantum-accelerated ML pipelines based on boson sampling are poised to achieve practical utility well before the realization of fault-tolerant universal quantum computers.