The Equational Theories Project: Advancing Collaborative Mathematical Research at Scale (2512.07087v1)

Abstract: We report on the Equational Theories Project (ETP), an online collaborative pilot project to explore new ways to collaborate in mathematics with machine assistance. The project successfully determined all 22 028 942 edges of the implication graph between the 4694 simplest equational laws on magmas, by a combination of human-generated and automated proofs, all validated by the formal proof assistant language Lean. As a result of this project, several new constructions of magmas satisfying specific laws were discovered, and several auxiliary questions were also addressed, such as the effect of restricting attention to finite magmas.

• The paper introduces a scalable, machine-assisted framework for formalizing 4,694 equational laws in magmas using Lean.
• It employs automated theorem proving, algebraic rewriting, and finite model enumeration to verify and partition the implication graph.
• The work sets new benchmarks in collaborative mathematical formalization by integrating human insights with robust computational methods.

The Equational Theories Project: Large-Scale Collaborative Formalization of Implication Graphs in Universal Algebra

Project Scope and Mathematical Foundations

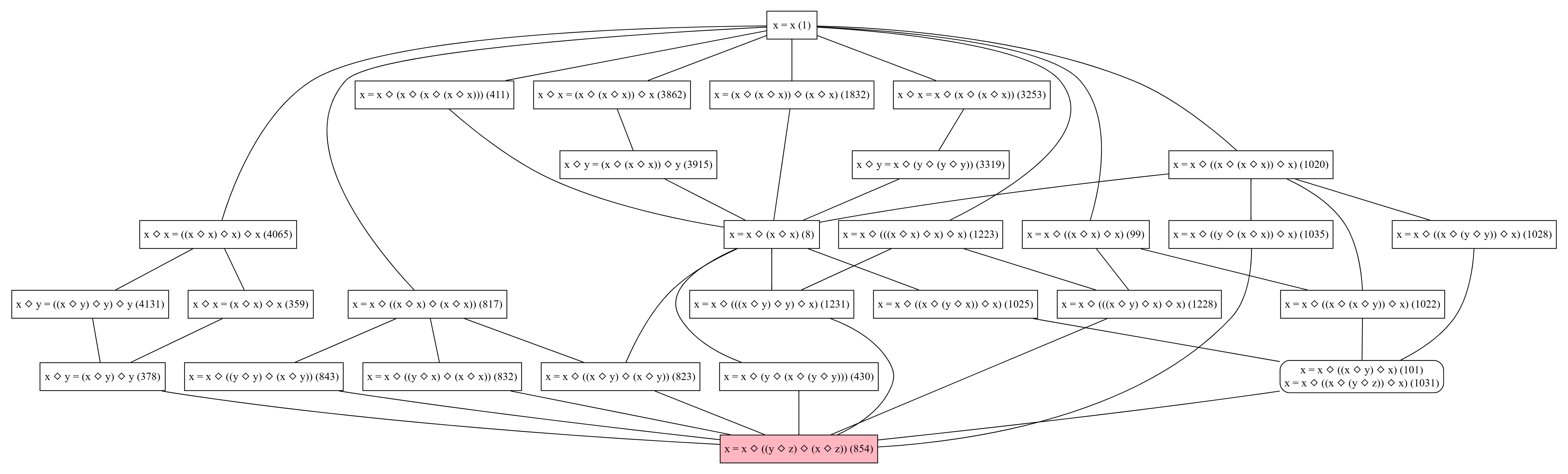
The Equational Theories Project (ETP) constitutes a major pilot experiment in scalable, machine-assisted collaboration on mathematical research, specifically targeting the systematic determination and formalization of the implication relations between $\num{4694}$ simplest equational laws on magmas. The effort involved characterizing all $\num{22028942}$ possible implication edges in the directed graph relating these laws, for both arbitrary and finite magmas, and formalizing proofs or counterexamples for each implication within the Lean proof assistant ecosystem.

The mathematical focus of ETP is universal algebra, exploiting the simplicity but nontrivial combinatorial interactions between equational laws involving binary operations (magmas). Each law, indexed as $E\{n\}$, is an identity between formal expressions in the magma operation. The main relation under investigation is logical implication among such laws: $E \models E'$ denotes that any magma satisfying $E$ must also satisfy $E'$. The investigation also considers the restricted version for finite magmas, $E \models_{\text{fin}} E'$, with attention to subtle breakdowns of classical theorems (e.g., Birkhoff completeness) in the finite regime.

Determination and Structure of the Implication Graph

ETP succeeded in determining—explicitly and with Lean-formalized certificates—all nonreflexive implications in the graph spanning the $4694$ laws, except for exactly two finite-magma implications, which remain conjectured false. The graph was then further partitioned into equivalence classes, revealing significant symmetries and large trivial equivalence classes (e.g., $1496$ laws equivalent to the singleton law).

Primary techniques for positive implications include:

• Algebraic rewriting and procedural reductions, reducing the search space through simple structural analysis.
• Exploiting duality and preorder symmetries to minimize direct proof obligations.
• Automated theorem proving (ATP), allowing bulk mechanized verification.
• Specialized finite techniques derived from function theory (surjectivity/injectivity equivalence).
• Canonical counterexample mining using ATPs for the negative implications.

  Figure 1: A Hasse diagram of all the equational laws implied by $E{854}$, emphasizing equivalence class structure and implication hierarchy.

Some implications—particularly counterexamples—required intricate constructions spanning finite model enumeration, linear/algebraic models ($x * y = ax + by$), translation-invariant magmas, semigroup twisting, greedy infinitary construction techniques, and ad hoc modifications to base magmas. Certain implication pairs were shown to be “immune” to broad classes of standard constructions, necessitating highly custom solutions.

Figure 2: Hasse diagrams contrasting the implication graphs for $E_{1729}$ for unrestricted versus finite magmas, showcasing increased implication density in the finite context.

Proof Formalization, Lean Engineering, and Collaboration Infrastructure

Central to the project’s approach is the rigorous formalization in Lean 4, necessitating scalable project management and a robust verification pipeline. The effort comprehensively integrated externally generated (e.g., ATP, SAT, SMT) results, human-generated blueprints, and automatic theorem certification within Lean, coupled with CI-based validation and multiple kernel-replay systems for safety.

Formalization engineering innovations included:

• A custom attribute tagging system for equational results, enabling systematic tracking of formalization status.
• Dual syntactic and semantic implementations of magma laws to facilitate both metatheoretic reasoning and concrete implication proofs.
• Automated theorem certificate parsing and translation from ATP output (Vampire, Prover9, Mace4, egg), with explicit reconstruction of proof steps in Lean (e.g., superposition, congruence closure).
• Project management via GitHub Issues, PR-driven modularization, automated CI-based progress updates, and visualization tools for implication graphs and dashboarding.

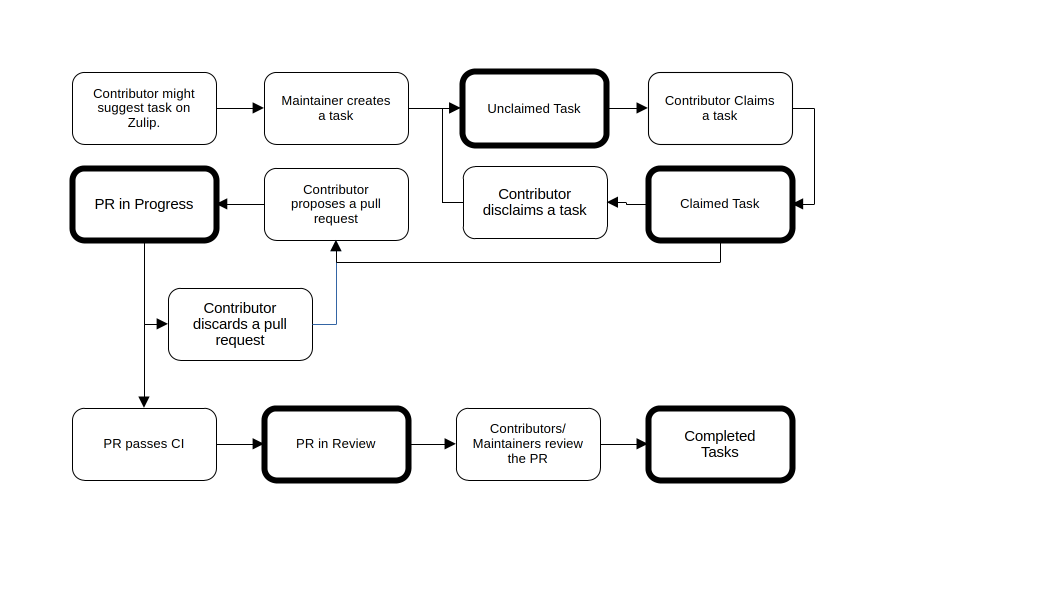
  Figure 3: Project management workflow chart, integrating Lean Zulip discussions, blueprint drafting, task claiming, and automated verification/merging on GitHub.

  

  Figure 4: Snapshot of ETP’s GitHub project dashboard, illustrating real-time progress tracking across task columns and user activities.

Techniques for Construction and Refutation

The project thoroughly systematized and formalized an array of counterexample and refutation methods, including:

• Exhaustive enumeration of finite magmas up to size 4, bracketing $>96\%$ of all false implications.
• Linear, affine, and translation-invariant models, leveraging algebraic varieties and functional equations for systematic counterexample generation.
• Greedy infinitary constructions, formalized as direct limits of partial magmas, achieving abstract non-implication results that are inherently non-finitary.
• Cohomological extensions and twisting semigroups, enabling counterexamples in “higher” algebraic structure.
• Syntactic invariants and canonizers, leveraging the structure of free magmas and term rewriting systems for non-implication by matching properties and normal form analysis.
• Automated proof guidance with semi-automated ATP filtering and input heuristics, including details on weight and clause management in ATPs.

  Figure 5: Visualization of $E_{854}$-type equations, central in the canonizer and unique factorization analysis.

Automated Theorem Proving and Integration

A substantial part of ETP's achievement lies in benchmark-scale integration of ATPs and SMTs. Key observations:

• Saturation-based systems (Vampire, Prover9) efficiently settled millions of implications with suitable search space parameterization.
• Model builders (Mace4) excelled for finite counterexample mining at scale.
• Proof certificates were algorithmically reconstructed into Lean proofs, preserving stepwise semantics.
• Weight, SOS limits, and ordering parameters critically influenced ATP throughput and solution quality.
• Empirical insights into tool complementarity and optimal configuration were distilled for future ATP-assisted research.

  Figure 6: Example of a reconstructed Vampire proof, showing structured contradiction via Lean superpose/subsumption combinatorics.

  

  Figure 7: MagmaEgg output reconstructing equational reasoning with reflexivity, symmetry, transitivity, and congruence.

  

  Figure 8: Human-readable Lean proof via egg+calcify tactic, clarifying rewrite sequencing for equational deduction.

Theoretical Discoveries and Spin-off Directions

ETP led to the discovery and classification of novel algebraic structures (e.g., weak central groupoids), refined spectrum analysis of laws (full spectrum vs. finite-only models), and revitalization of single-law characterizations for classical structures (groups, Boolean algebras).

Central open questions emanate regarding undecided finite implications (notably, $E_{677} \models_{\text{fin}} E_{255}$), irreducibility of implications, non-trivial infinite models, surjunctivity, stability/mutability of laws under perturbation, explicit free magma construction, and extension to multi-law logical relations.

Machine learning experiments with CNN architectures suggest feasible extrapolation and compression of the implication graph, with surprising accuracy even at low training set proportions; future investigations may hinge on differentiability between structural learning versus transitive closure encoding.

Interface, Visualization, and Data Stewardship

Custom web-based tools—dashboard, equation explorer, Graphiti, Finite Magma Explorer—enabled direct community engagement and real-time progress tracking. All data, formalizations, and proofs are public and versioned on GitHub, with revelation of underlying Lean objects and full reproducibility.

Figure 9: Equation Explorer interface delivering inbound/outbound implications, equivalence class enumeration, and commentary per law.

Conclusion

ETP demonstrates the feasibility and scalability of large, open, modular crowdsourced mathematical formalization projects at computational scale. Combining human, AI, and ATP strengths, together with lean-programmed verification and robust infrastructure, the project establishes benchmarks for methodology, reproducibility, and collaborative knowledge management. The spectrum of techniques—algorithmic, syntactic, cohomological, and probabilistic—underscore the necessity of heterogeneous approaches in comprehensive mathematical formalization.

Going forward, the ETP paradigm sets a precedent for future collaborative endeavors aiming at systematic exploration and formal certification of massive logical spaces, with significant ramifications for universal algebra, AI-assisted mathematics, benchmark automation, and mathematical data science.