Geometric Optimization on Lie Groups: A Lie-Theoretic Explanation of Barren Plateau Mitigation for Variational Quantum Algorithms (2512.02078v1)

Abstract: Barren plateaus, which means the training gradients become extremely small, pose a major challenge in optimizing parameterized quantum circuits, often making the learning process impractically slow or stall. This work shows why using neural networks to generate quantum circuit parameters helps overcome this difficulty. We introduce a geometric viewpoint that describes how the parameters produced by neural networks evolve during training. Our analysis shows that these parameters follow smooth and efficient paths that avoid the flat regions in the training that cause barren plateaus. This provides a computational explanation for the improved trainability observed in recent neural network-assisted quantum learning methods. Overall, our findings bridge ideas from quantum machine learning and computational optimization, offering new insight into the structure of quantum models and guiding future approaches for designing more trainable quantum circuits or parameter initialization.

• The paper shows that neural network-generated parameter trajectories follow near-geodesic paths on SU(2) to mitigate barren plateaus.
• It employs Lie groups and algebra methodologies to quantify velocity, acceleration, and energy metrics for efficient quantum optimization.
• The study provides guidelines for designing VQA architectures and initialization strategies using manifold-constrained optimization techniques.

Geometric Optimization on Lie Groups for Barren Plateau Mitigation in Variational Quantum Algorithms

Introduction

This work presents a rigorous Lie-theoretic framework to analyze and explain how neural-network-generated quantum circuit parameters mitigate the barren plateau phenomenon in variational quantum algorithms (VQAs) (2512.02078). Barren plateaus, marked by exponentially vanishing gradients as qubit number increases, have hindered the scalability and practicality of VQAs for quantum machine learning and combinatorial optimization. Conventional strategies to address these issues, such as hardware-efficient ansatz design, advanced initialization protocols, and engineered dissipation, have provided partial relief but lack a comprehensive mathematical justification for the empirically observed advantages of neural network-based parameter generators.

Leveraging the structure of the special unitary group $\mathbb{SU}(2)$ and its Lie algebra $\mathfrak{su}(2)$, this paper establishes a geometric correspondence between quantum gate parameter trajectories and geodesics on the group manifold. The authors argue that neural network-generated parameter sequences evolve along nearly geodesic paths, thereby avoiding the flat, high-curvature regions of the optimization landscape that lead to barren plateaus. This insight not only clarifies the underlying mechanism for improved trainability but also offers guidance for future architecture and initialization design.

Mathematical Framework: Lie Groups and Quantum Gates

The authors articulate the connection between single-qubit rotation gates and the $\mathbb{SU}(2)$ Lie group by expressing gate operations as exponentials of $\mathfrak{su}(2)$ algebra elements. Each rotation, such as $R_x(\theta)$, $R_y(\theta)$, and $R_z(\theta)$, is parametrized as $\exp(-i\theta\sigma_j/2)$, mapping directly into the group structure and facilitating a natural geometric interpretation of gate transformations.

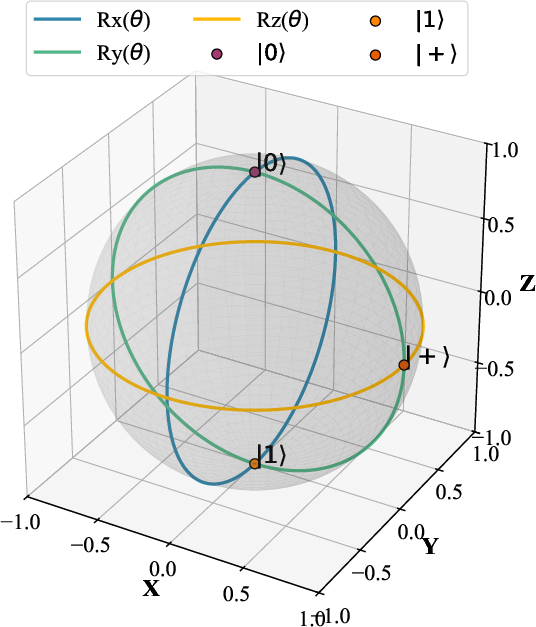
Figure 1: Geometric representation of single-qubit rotation gates on the Bloch sphere. Each trajectory shows the operation of $R_{x}(\theta)$, $R_{y}(\theta)$, and $R_{z}(\theta)$ as $\mathbb{SU}(2)$ elements.

By leveraging the exponential map $\exp: \mathfrak{su}(2) \to \mathbb{SU}(2)$ and the bi-invariant Riemannian metric on $\mathbb{SU}(2)$, the authors define geodesic evolution as the most efficient (shortest, minimal energy) trajectory for parameter optimization. The analysis extends to time-dependent parameter functions $\theta(t)$, with velocity and acceleration metrics quantifying deviations from the ideal geodesic path. The explicit form of these trajectories highlights the importance of maintaining low curvature and bounded fluctuations in parameter evolution to guarantee smooth optimization dynamics.

Neural Network Parameter Generation and Fluctuation Analysis

Empirical results demonstrate that neural networks produce parameter updates that closely track geodesics, with minimal fluctuation, velocity, and acceleration. A detailed comparison of parameter trajectories generated with and without neural network modules shows significant differences in regularity and stability.

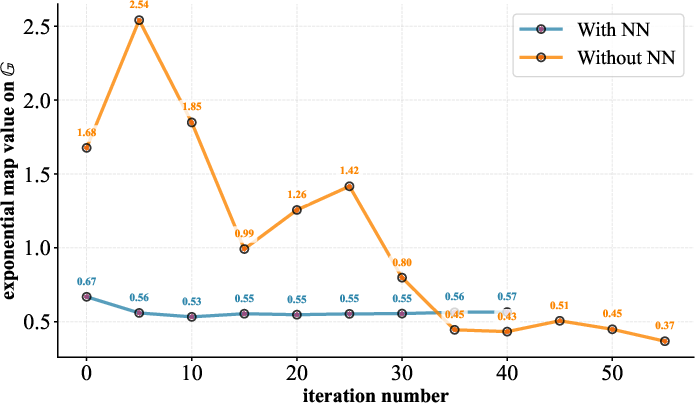
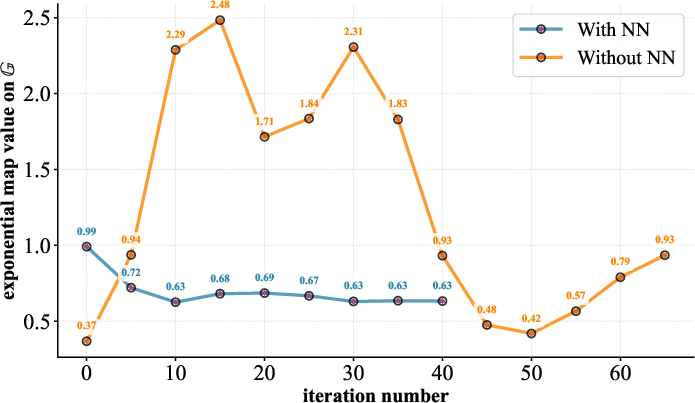
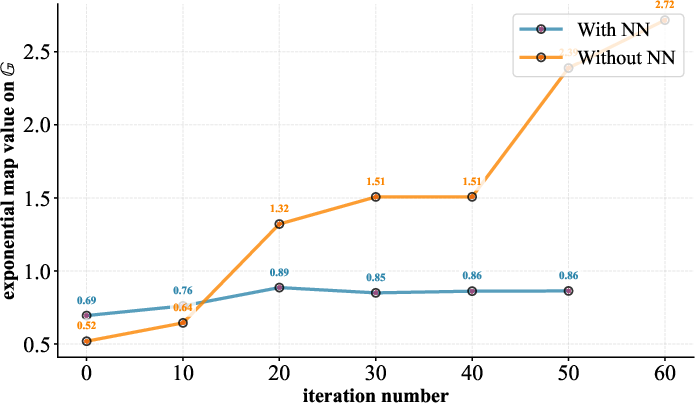
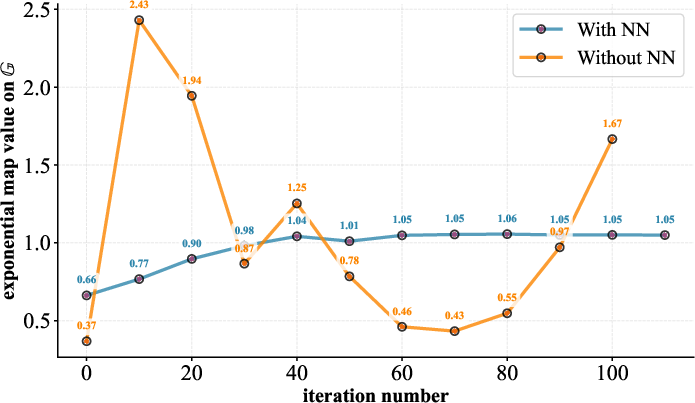
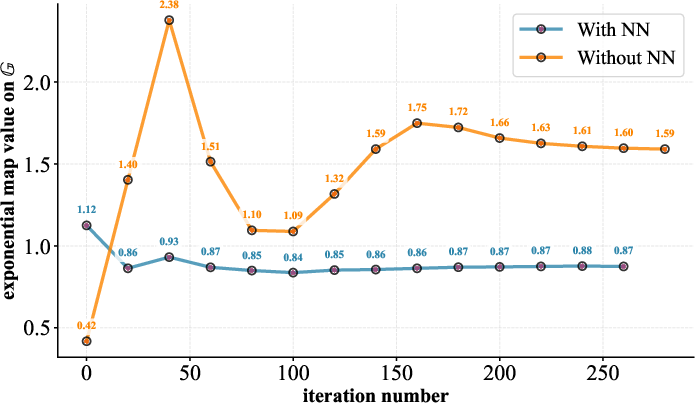
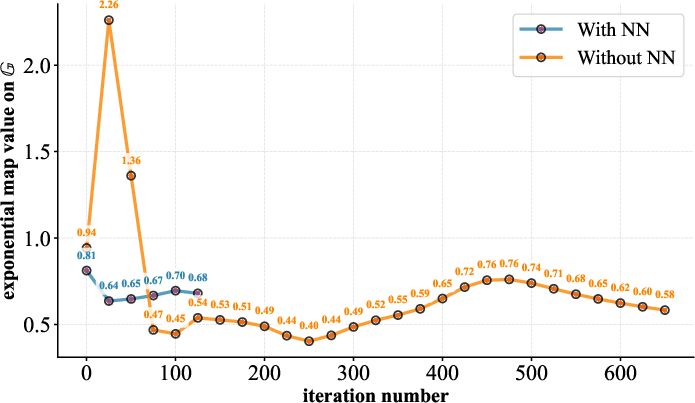
Figure 2: Fluctuation comparison of the group-mapped value with and without the neural-network module; neural networks reduce trajectory fluctuation and barren plateau occurrence.

When neural networks are used to generate quantum circuit parameters, the resulting trajectories show reduced fluctuation patterns over optimization iterations. This manifests as smoother parameter updating—an alignment with the manifold’s geodesic structure. In contrast, randomly initialized or unconstrained updates introduce pronounced instability, leading to inefficient exploration of the parameter space and increased susceptibility to barren plateaus.

Dynamics: Velocity, Acceleration, and Manifold Stability

Quantitative analysis of velocity and acceleration profiles illustrates stark improvements in the stability of neural network-enhanced models. For systems with 4 to 9 qubits, average velocity ($\overline{v}$) and acceleration ($\overline{a}$) are consistently closer to zero when neural networks are employed. This implies that the parameter evolution adheres closely to geodesic paths on $\mathbb{SU}(2)$, with lower kinetic energy and trajectory length, supporting more efficient optimization and lower resource consumption.

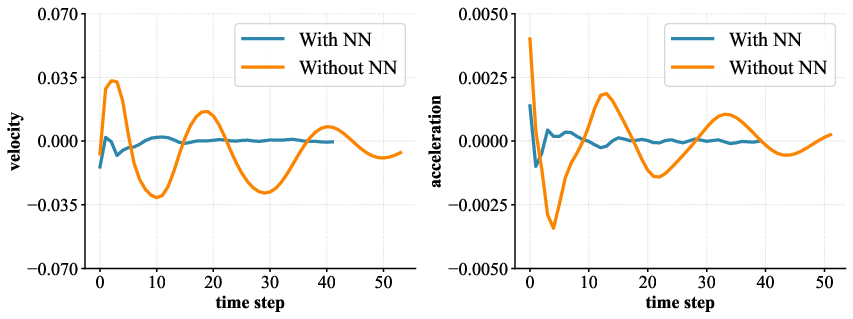
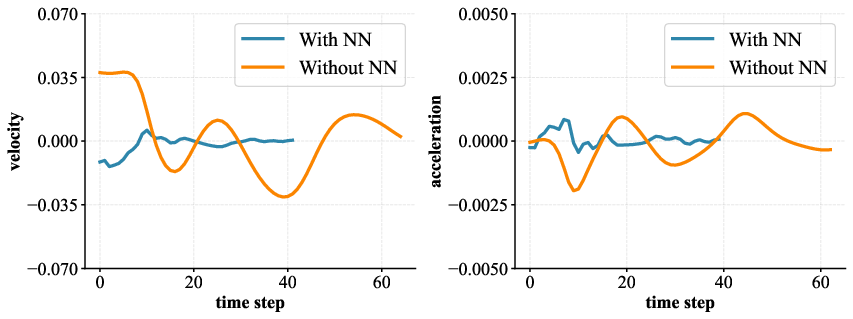
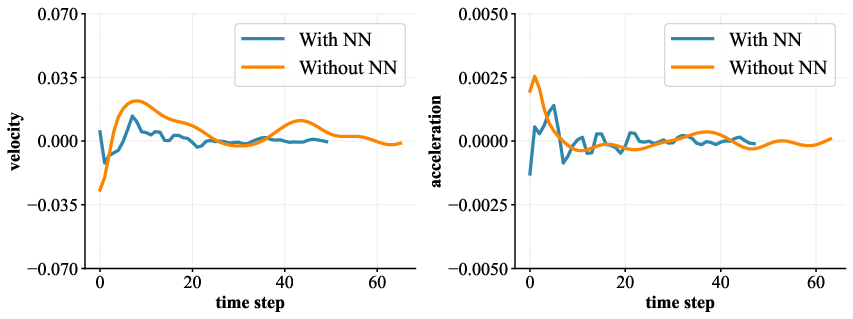
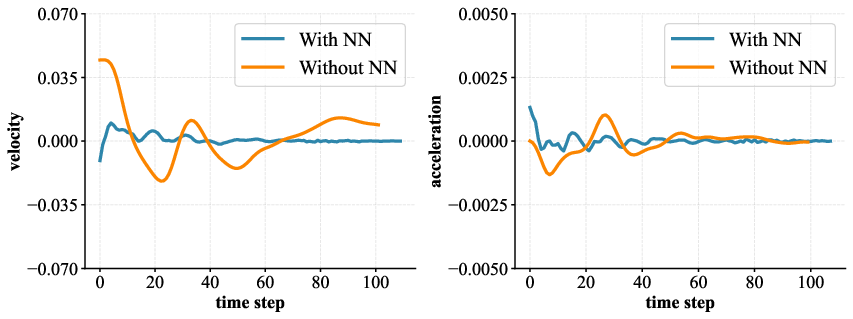
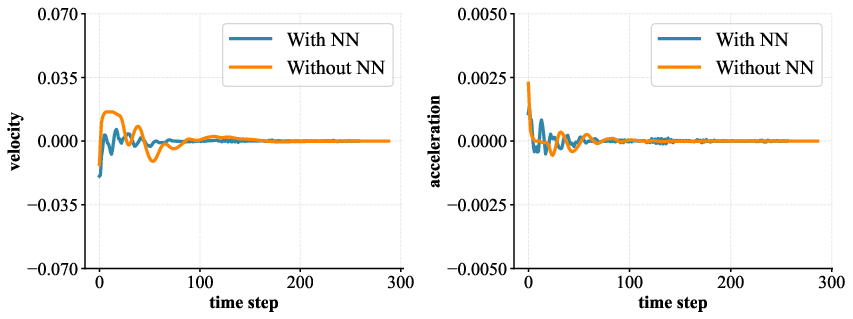
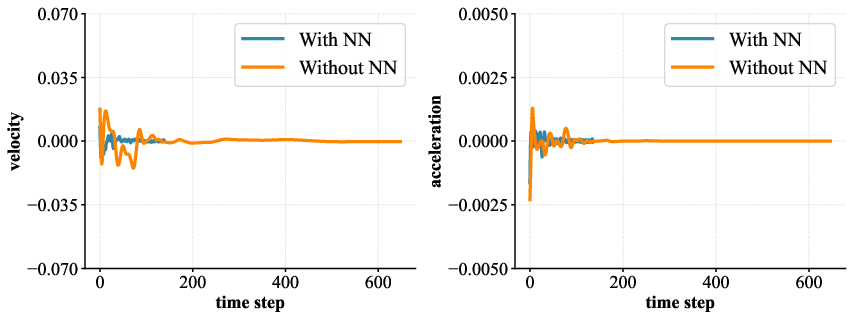
Figure 3: Comparison of the velocity and acceleration for models with and without neural network modules; neural networks maintain dynamical stability and near-zero slopes.

Additionally, the paper analyzes the energy $E$ and trajectory length $L$ for both models, revealing that neural network-based methods substantially lower both metrics across all qubit counts. The relative standard deviation (RSD) values, capturing the consistency of these trends, are similar for both strategies, suggesting that the primary advantage stems specifically from the alignment with geodesic dynamics rather than reduced variability alone.

Implications and Future Directions

The geometric characterization of parameter optimization links classical manifold-constrained optimization theory with quantum machine learning practice. This framework substantiates the claim that parameter trajectories generated by neural networks naturally avoid regions of high curvature and dead zones in the cost landscape—effectively circumventing the barren plateau pathology. Practically, this points to new algorithmic design paradigms for VQAs, such as:

• Leveraging manifold-constrained optimizers and parameter generators that explicitly enforce geodesic-like evolution on Lie groups.
• Informing parameter initialization and ansatz selection through Lie-theoretic metrics rather than heuristic or random approaches.
• Extending the geometric analysis to higher-dimensional unitary groups ($\mathbb{SU}(n)$, $n > 2$), facilitating implementation for multi-qubit gate operations and scalable quantum models.

The theoretical contribution also sets the stage for advanced studies concerning the generalization of these principles to complex non-Abelian symmetries, higher-order cost landscapes, and hybrid classical-quantum learning protocols.

Conclusion

This work provides a rigorous geometric and Lie-theoretic explanation for the mitigation of barren plateaus in VQAs through neural network parameter generation. By demonstrating that neural network-driven trajectories on $\mathbb{SU}(2)$ conform to near-geodesic paths—characterized by low energy, short path lengths, and dynamical stability—the authors supply strong mathematical support for improved convergence and resource efficiency. This approach suggests a principled direction for future quantum model design and lays the groundwork for broader applications in quantum learning and optimization.