High-dimensional Mean-Field Games by Particle-based Flow Matching (2512.01172v1)

Abstract: Mean-field games (MFGs) study the Nash equilibrium of systems with a continuum of interacting agents, which can be formulated as the fixed-point of optimal control problems. They provide a unified framework for a variety of applications, including optimal transport (OT) and generative models. Despite their broad applicability, solving high-dimensional MFGs remains a significant challenge due to fundamental computational and analytical obstacles. In this work, we propose a particle-based deep Flow Matching (FM) method to tackle high-dimensional MFG computation. In each iteration of our proximal fixed-point scheme, particles are updated using first-order information, and a flow neural network is trained to match the velocity of the sample trajectories in a simulation-free manner. Theoretically, in the optimal control setting, we prove that our scheme converges to a stationary point sublinearly, and upgrade to linear (exponential) convergence under additional convexity assumptions. Our proof uses FM to induce an Eulerian coordinate (density-based) from a Lagrangian one (particle-based), and this also leads to certain equivalence results between the two formulations for MFGs when the Eulerian solution is sufficiently regular. Our method demonstrates promising performance on non-potential MFGs and high-dimensional OT problems cast as MFGs through a relaxed terminal-cost formulation.

• The paper proposes a simulation-free, particle-based flow matching approach that recasts mean-field games in Lagrangian coordinates for high-dimensional settings.
• It uses alternating proximal gradient updates and neural flow matching to achieve convergence, with rates ranging from sublinear to exponential under strong convexity.
• Empirical results demonstrate state-of-the-art performance on image translation and dynamic optimal transport tasks, showcasing practical scalability in complex environments.

High-dimensional Mean-Field Games by Particle-based Flow Matching

Introduction

This paper develops a simulation-free, particle-based framework for efficiently solving high-dimensional first-order mean-field games (MFGs). MFGs paper Nash equilibria for large populations of interacting agents, formulated as fixed-point optimal control problems. Despite their theoretical unification of optimal transport (OT), generative models, and multi-agent control, computational tractability in high dimensions remains a significant challenge due to the curse of dimensionality, the structure of the fixed-point (non-variational) problem, and the cost of backpropagation through coupled PDE/ODE solvers.

The proposed method leverages a proximal fixed-point scheme in Lagrangian coordinates, alternating between particle updates (using gradient-based optimization) and training a flow neural network using a flow matching (FM) objective. This neural FM aligns the transported empirical particle velocities with a parameterized velocity field, achieving efficient, mesh-free optimization suitable for high-dimensional spaces.

Methodology

The central innovation consists of recasting MFGs within the Lagrangian (particle-based) framework, where each agent's state evolution is parameterized via sample trajectories. The overall scheme involves three main steps in each iteration:

1. Particle Optimization: Particles are updated via a proximal gradient descent on the agent cost, with respect to the current velocity field and interaction structure.
2. Neural Flow Matching: A flow neural network is trained (with mean-squared error loss) to regress and match the updated empirical velocities of the sample trajectories, providing a smooth parameterization of the control field.
3. Alternating Proximal Fixed-point Iterations: The algorithm proceeds via fictitious play-inspired iterations, seeking convergence to a Nash equilibrium by local (proximal) improvements.

The theoretical contribution establishes that under suitable regularity (convexity, smoothness), this algorithm enjoys sublinear convergence for generic optimal control objectives and linear (exponential) convergence under strong convexity assumptions. The analysis leverages a key property of flow matching: FM induces an Eulerian flow from Lagrangian particles, preserving or reducing the objective while maintaining consistency with the continuity equation.

Figure 1: Illustration of the intermediate distributions obtained by the proposed algorithm interpolating from a $4 \times 4$ checkerboard to an isotropic Gaussian.

Theoretical Analysis

The paper demonstrates an equivalence between Eulerian and Lagrangian MFG formulations under regular velocity fields, generalizing prior results beyond variational (potential) settings. Specifically, FM can be used to obtain a velocity field and density evolution $(\rho, v)$ from generic particle trajectories $X$ such that $(\rho, v)$ satisfies the continuity equation, and the cost $J(\rho, v; \rho)$ does not exceed $J(X; \rho)$. The converse also holds for regular velocities, supporting the claim that the proposed particle-based FM approach is theoretically robust even in high-dimensional, non-potential, and non-Eulerian cases.

The convergence proof analyzes the joint particle/flow-matching procedure as a generalized conditional gradient method in trajectory space, extending recent results connecting fictitious play and Frank-Wolfe approaches for MFGs. The method is shown to reduce the cost at each step, with explicit contraction rates hinging on the smoothness and convexity of the couplings.

Numerical Experiments

The empirical evaluation covers both synthetic and image domains, including dynamic OT with relaxed terminal costs (KL divergence), image-to-image translation between complex, high-dimensional distributions, and genuinely non-potential MFGs with asymmetric coupling. The proposed method is compared against leading neural optimal transport solvers, flow-based conditional transport, GAN-based translators, and actor-critic MFG solutions.

Image-to-Image Translation: The method achieves state-of-the-art FID on the handbag-to-shoes and CelebA male-to-female translation benchmarks, matching or outperforming strong OT-based and GAN-based baselines. Notably, the approach yields smooth, coherent interpolations with strong visual consistency.

Figure 2: Example result: Handbags to Shoes translation illustrates visually coherent and consistent sample trajectories produced by the Flow Matching-based MFG approach.

Toy High-dimension OT: The checkerboard and isotropic Gaussian example (shown previously) visualizes the evolving marginal distributions at intermediate times, demonstrating smooth alignment and convergence of particle densities under the learned flow.

Non-potential MFG: The algorithm achieves rapid convergence of the Nash-residual, confirming proximity to fixed points even when the MFG lacks a variational structure.

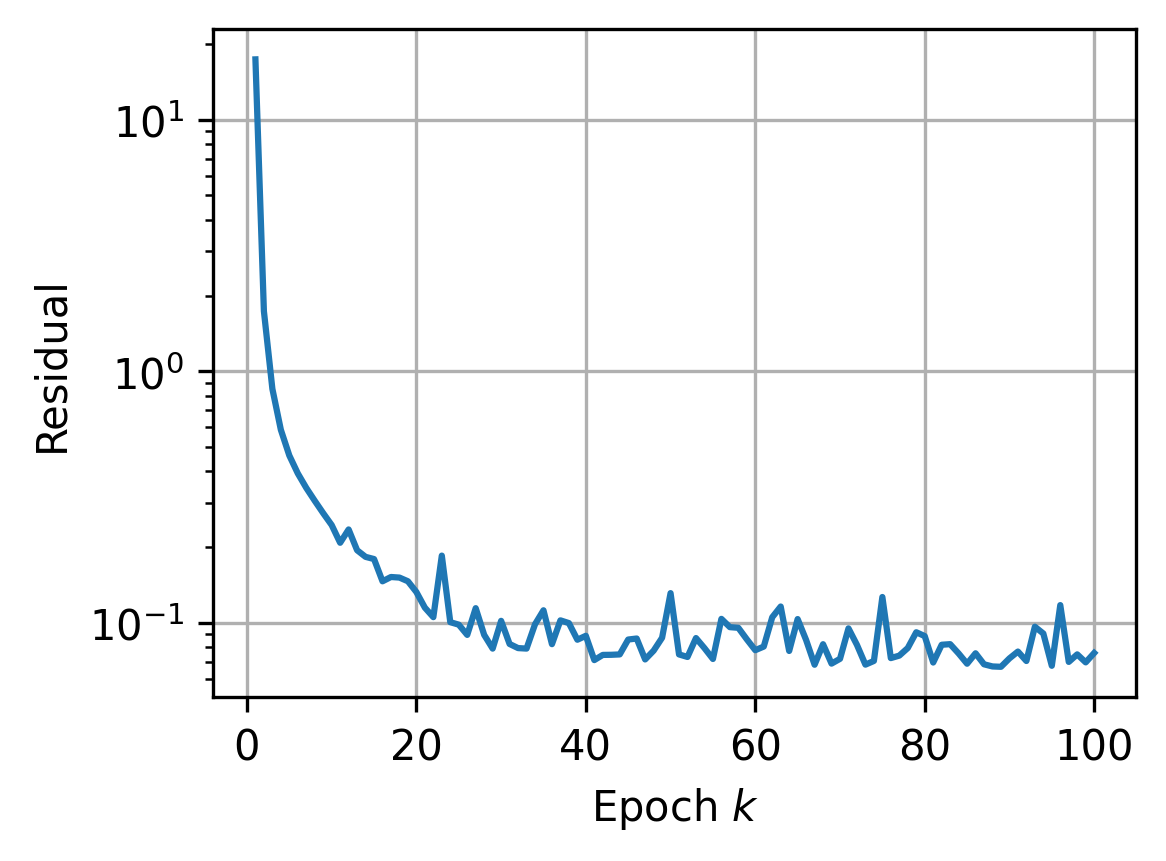
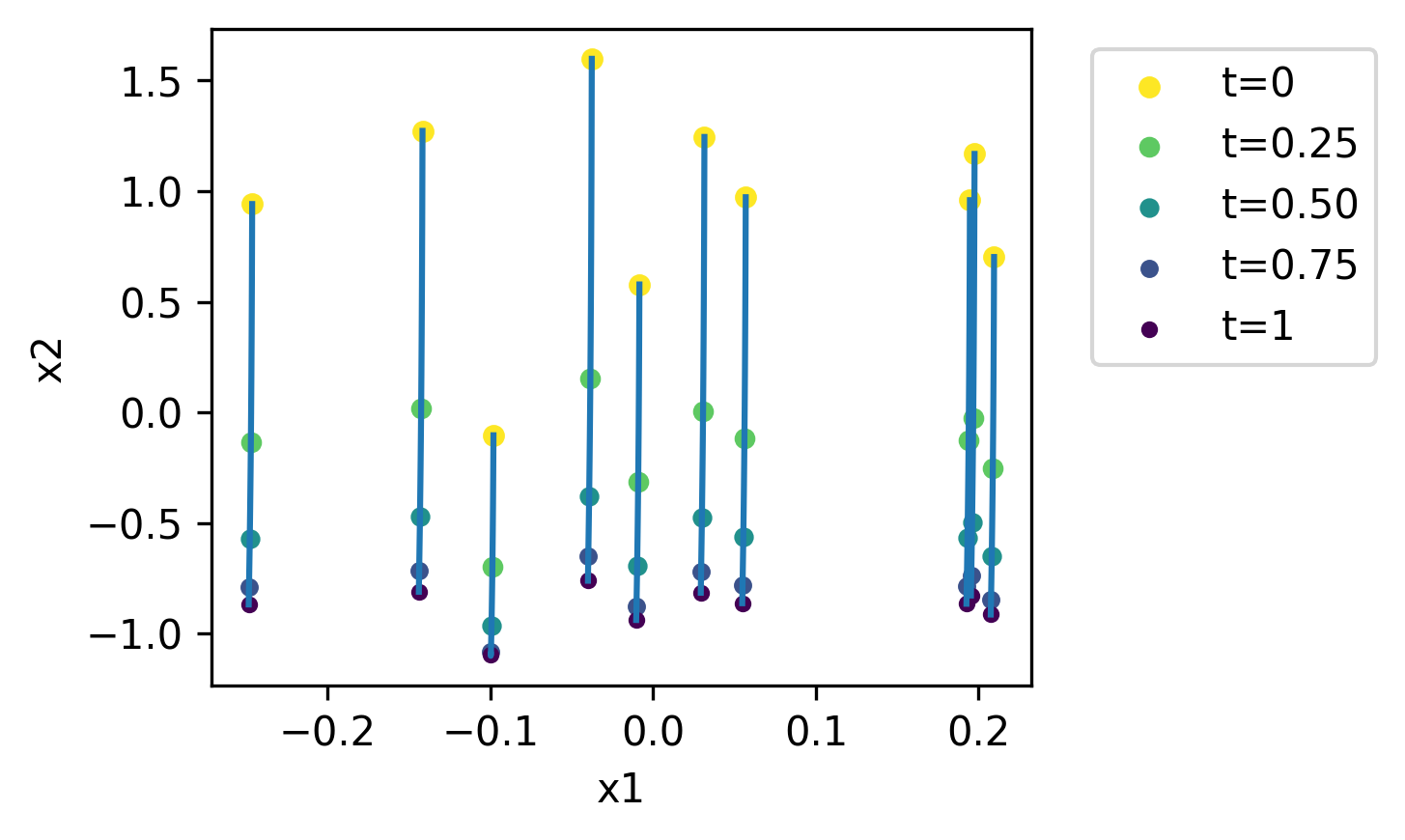
Figure 3: Plot of the Nash residual over training epochs for a non-potential MFG, demonstrating effective convergence of the particle-based FM algorithm.

Implications and Future Directions

This approach establishes that particle-based FM can provide scalable, theoretically sound, simulation-free optimization for high-dimensional MFGs, overcoming some limitations of mesh-based and PDE-solver approaches. Practical implications include more efficient generative modeling, scalable solution of control and transport problems, and a pipeline compatible with modern deep learning infrastructure.

The work opens several directions for further research. Memory requirements for storing trajectory populations may become substantial for very large agent sets or fine temporal discretizations. Extending theoretical convergence to fully general (including non-potential, nonconvex) MFGs and handling standing errors (from discrete optimization, sampling, and neural network approximation) are natural next steps. The framework invites further experimentation on real-world datasets and applications across economics, engineering, and machine learning, particularly for tasks involving large-scale population dynamics, generative modeling, or robust optimal control.

Conclusion

This paper develops and analyzes a computationally practical, scalable framework for solving high-dimensional MFGs using particle-based flow matching. The method provides a mesh-free, simulation-free, and theoretically justified approach—supported by strong empirical performance on OT, image translation, and non-potential games. The demonstrated equivalence between Eulerian and Lagrangian perspectives in this setting, together with robust convergence properties for the proposed scheme, underline its potential as a fundamental tool for high-dimensional control and generative modeling problems.