A Survey on Centrality and Importance Measures in Hypergraphs: Categorization and Empirical Insights (2512.00107v1)

Abstract: Identifying central entities and interactions is a fundamental problem in network science. While well-studied for graphs (pairwise relations), many biological and social systems exhibit higher-order interactions best modeled by hypergraphs. This has led to a proliferation of specialized hypergraph centrality measures, but the field remains fragmented and lacks a unifying framework. This paper addresses this gap by providing the first systematic survey of 39 distinct measures. We introduce a novel taxonomy classifying them as: (1) structural (topology-based), (2) functional (impact on system dynamics), or (3) contextual (incorporating external features). We also present an experimental assessment comparing their empirical similarity and computation time. Finally, we discuss applications, establishing a coherent roadmap for future research in this area.

• The paper proposes a taxonomy categorizing 39 hypergraph centrality measures into structural, functional, and contextual groups.
• It conducts extensive empirical analyses across real-world datasets, revealing significant ranking variations and scalability tradeoffs.
• The survey underscores the need for methodological transparency and standardized frameworks in selecting hypergraph centrality measures.

Systematic Survey of Hypergraph Centrality and Importance Measures

Introduction and Motivation

Hypergraphs, as a generalization of graphs allowing higher-order (non-dyadic) interactions, are crucial for modeling complex systems found in biological, social, infrastructure, and information networks. Classical centrality measures—such as degree, closeness, and betweenness—are well-developed in the context of pairwise graphs; however, their extension to hypergraphs presents new theoretical and computational challenges. The surveyed paper offers a comprehensive and structured taxonomy of 39 different hypergraph centrality and importance measures, proposes a principled classification, and conducts extensive empirical studies to compare the behavior and efficiency of representative measures (2512.00107).

Taxonomy of Hypergraph Centrality and Importance Measures

The work introduces a tripartite taxonomy for hypergraph measures:

1. Structural Measures: These rely solely on hypergraph topology, considering elements like degrees, walks, paths, or subhypergraphs.
2. Functional Measures: These quantify importance based on an entity’s impact on the system—typically via perturbation analyses (e.g., removal of nodes/hyperedges) or game-theoretical coalition value allocations.
3. Contextual Measures: These integrate external information (node/hyperedge features, labels, or learned representations), allowing the measure to reflect both topological structure and associated metadata.

The categorization clarifies methodological foundations and highlights the limitations and applicability of each family of measures. A schematic example is provided to illustrate the variety of perspectives yielded by different centrality definitions; for instance, betweenness versus hypercoreness may prioritize structurally distinct nodes.

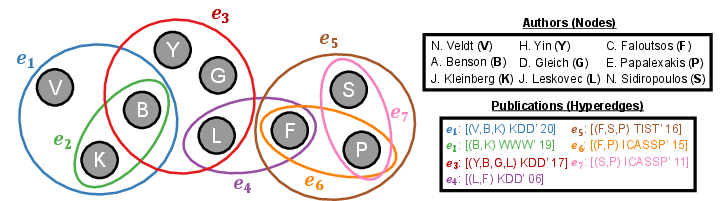
Figure 1: Example co-authorship hypergraph, with nodes as authors and hyperedges as publications; distinct centrality measures yield different node rankings.

Representative Classes and Foundational Insights

The survey catalogues the landscape of hypergraph measures in technical detail, including:

• Degree-based (e.g., node degree and neighbor-degree): Simple and computationally efficient; may fail to capture nonlocal or groupwise relevance.
• Path-based (e.g., closeness, betweenness, harmonic centrality): Sensitive to definitions of walks and paths in hypergraphs, often computationally expensive.
• Walk/spectral-based (e.g., various tensorized eigenvector definitions, random-walk variants): Capture global structural influence but introduce significant complexity—especially when addressing non-uniform hyperedge cardinalities.
• Subhypergraph-based (e.g., hypercore, trussness, motifs): Reveal dense or functionally cohesive regions; empirical analysis demonstrates that these often provide orthogonal insights compared to path or degree-based measures.

Novel measures that incorporate features and roles, such as matrix centrality or attention-based mechanisms in hypergraph neural networks, are also discussed, representing a shift toward data-driven and context-aware methodologies.

Empirical Analyses: Correlation and Scalability

A comprehensive empirical assessment is conducted, covering ten real-world datasets (from bills and e-mails to biological and infrastructure networks) and ten representative measures. The analysis focuses on the similarity of rankings produced by different measures, as well as their computational efficiency.

Key numerical and empirical findings:

• Global Correlation: High overall agreement in broad trends (average Spearman coefficients: 0.773 for nodes, 0.434 for hyperedges; see Figure 2 and Figure 3), but limited concordance among the top-ranked entities (Jaccard similarity @ 5%: 0.443 for nodes, 0.271 for hyperedges).
• Clustering of Measures: Many measures fall into consistent methodological clusters (e.g., neighbor-degree, closeness, and harmonic centralities; degree and betweenness centralities), but some—such as hypercoreness or eigenvector centrality—act as distinct singletons, revealing that they capture unique structural aspects not well represented by other measures.

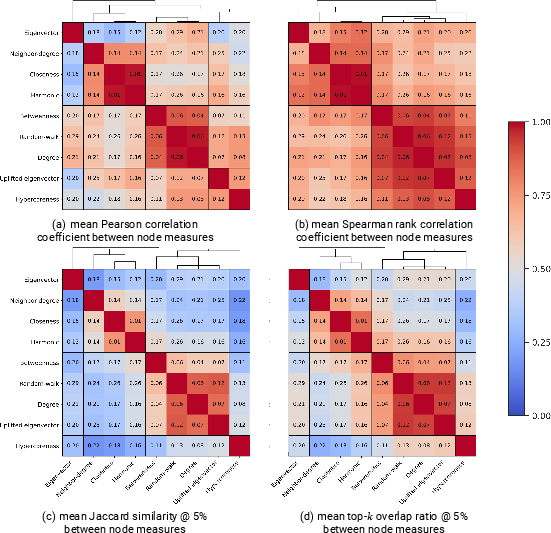
  Figure 2: Correlation of node centrality measures across metrics; strong intra-cluster agreements and marked outliers.

  

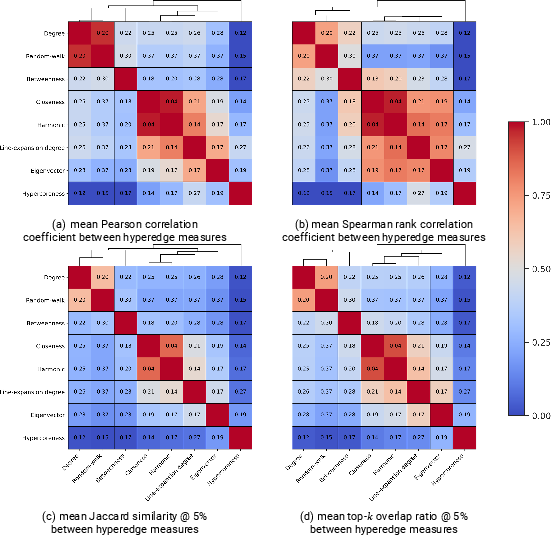
  Figure 3: Correlation of hyperedge centrality measures; functional divergence notably higher than for node measures.

• Scalability and Runtime: Degree-based measures exhibit sublinear scaling with the number of nodes or hyperedges, making them suitable for large-scale hypergraphs. In contrast, path-based and subhypergraph-based measures are often superquadratic and become infeasible at scale; for example, path-based measures can require several days for computation even on moderate-sized instances.

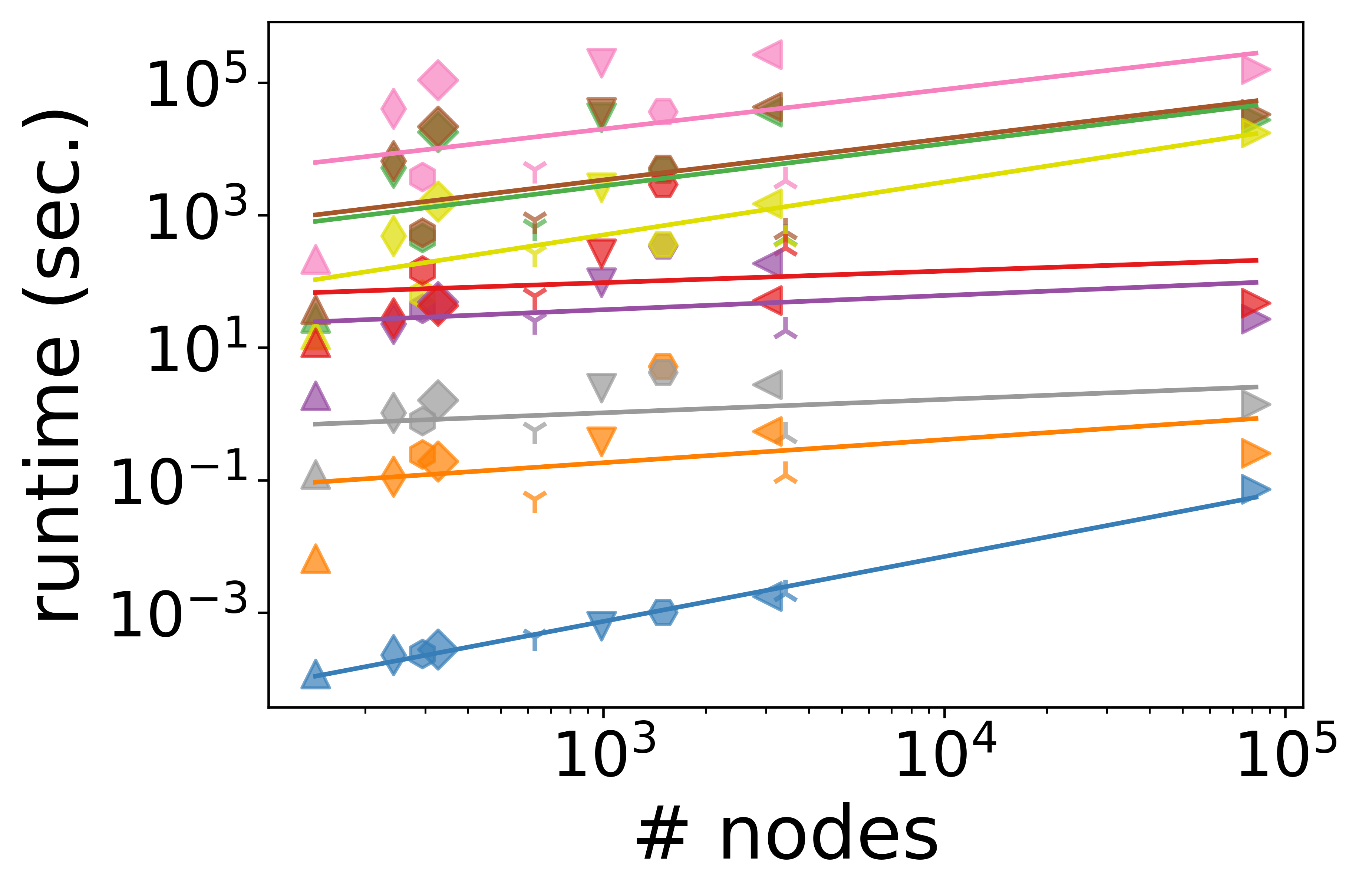
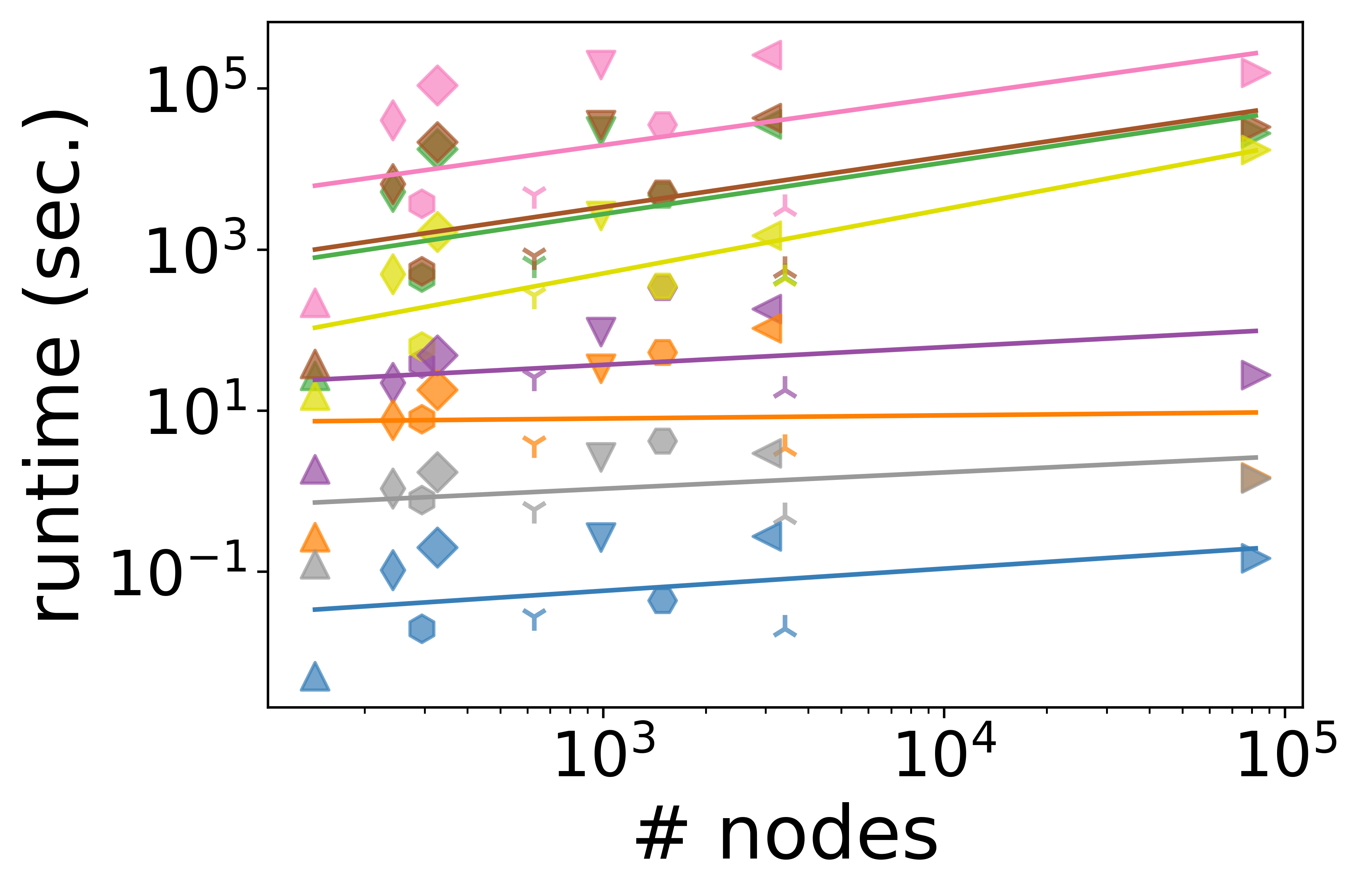
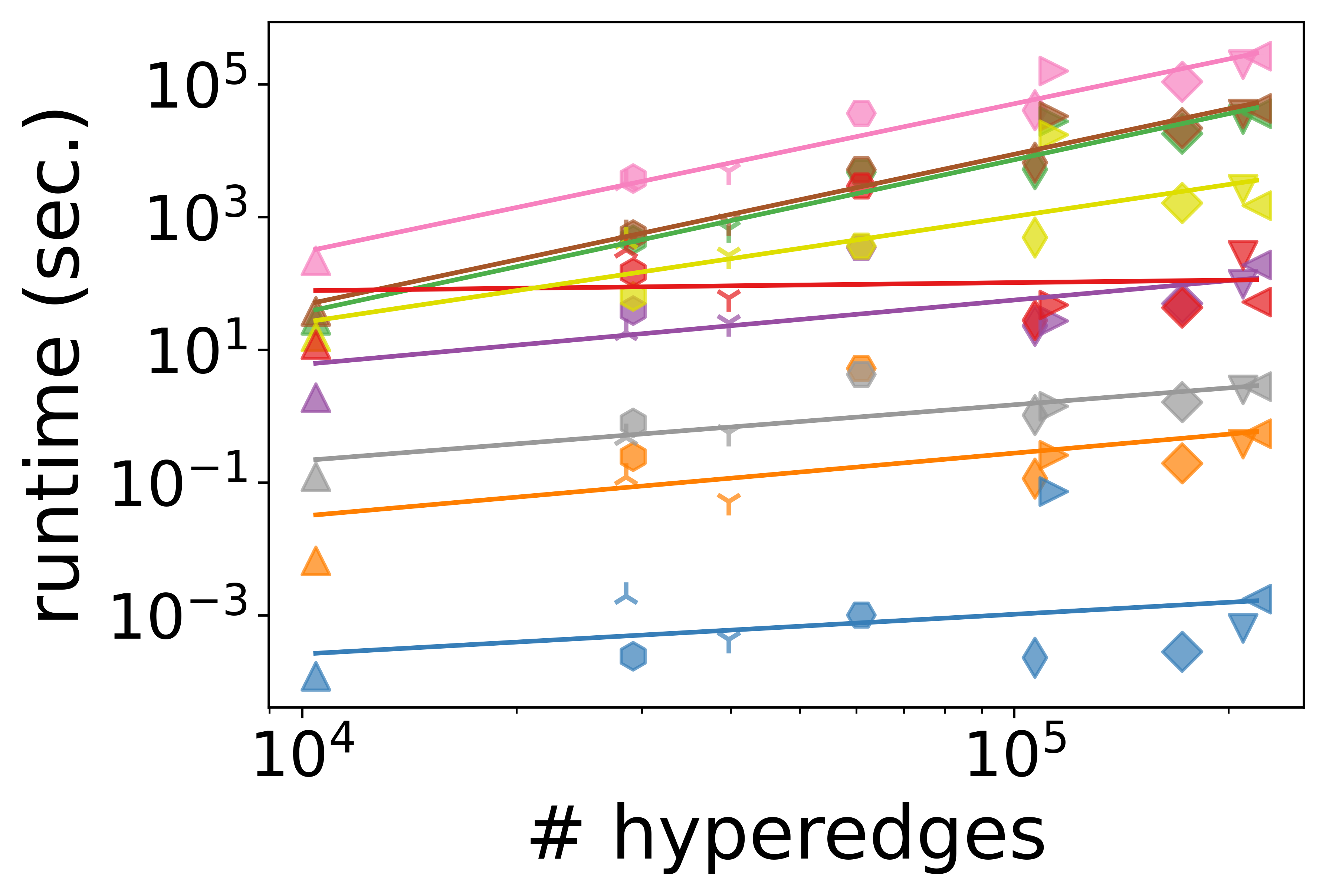
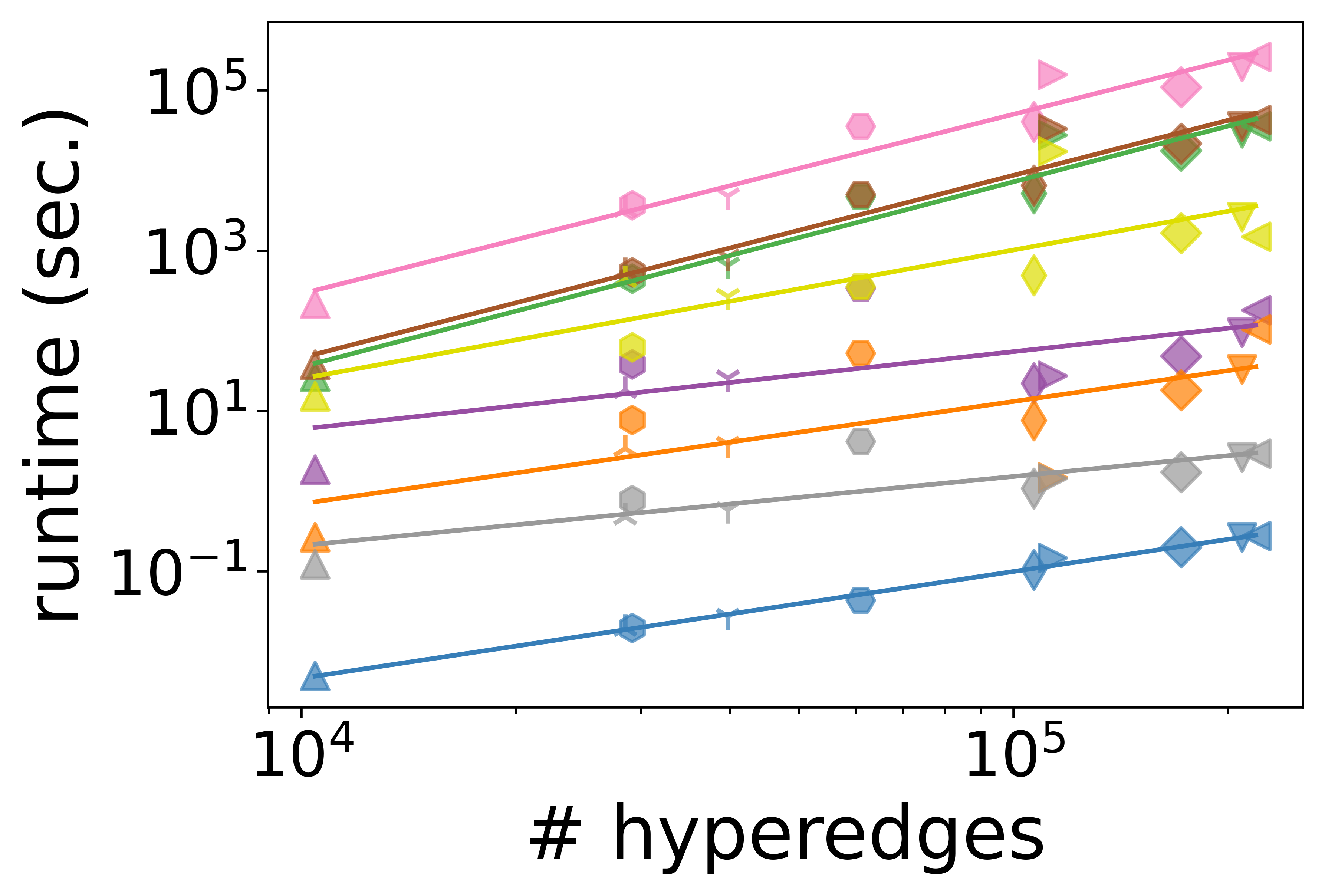
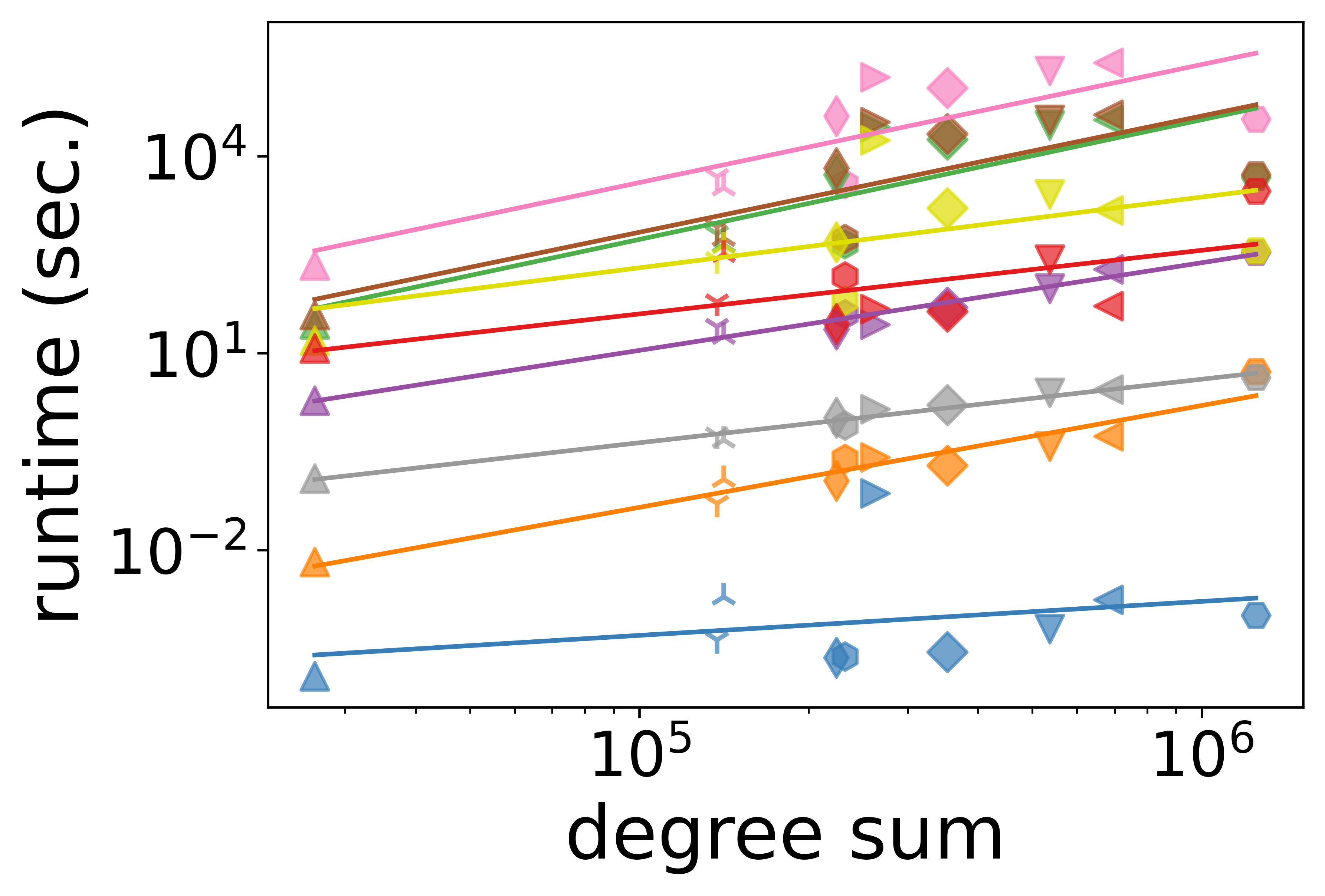
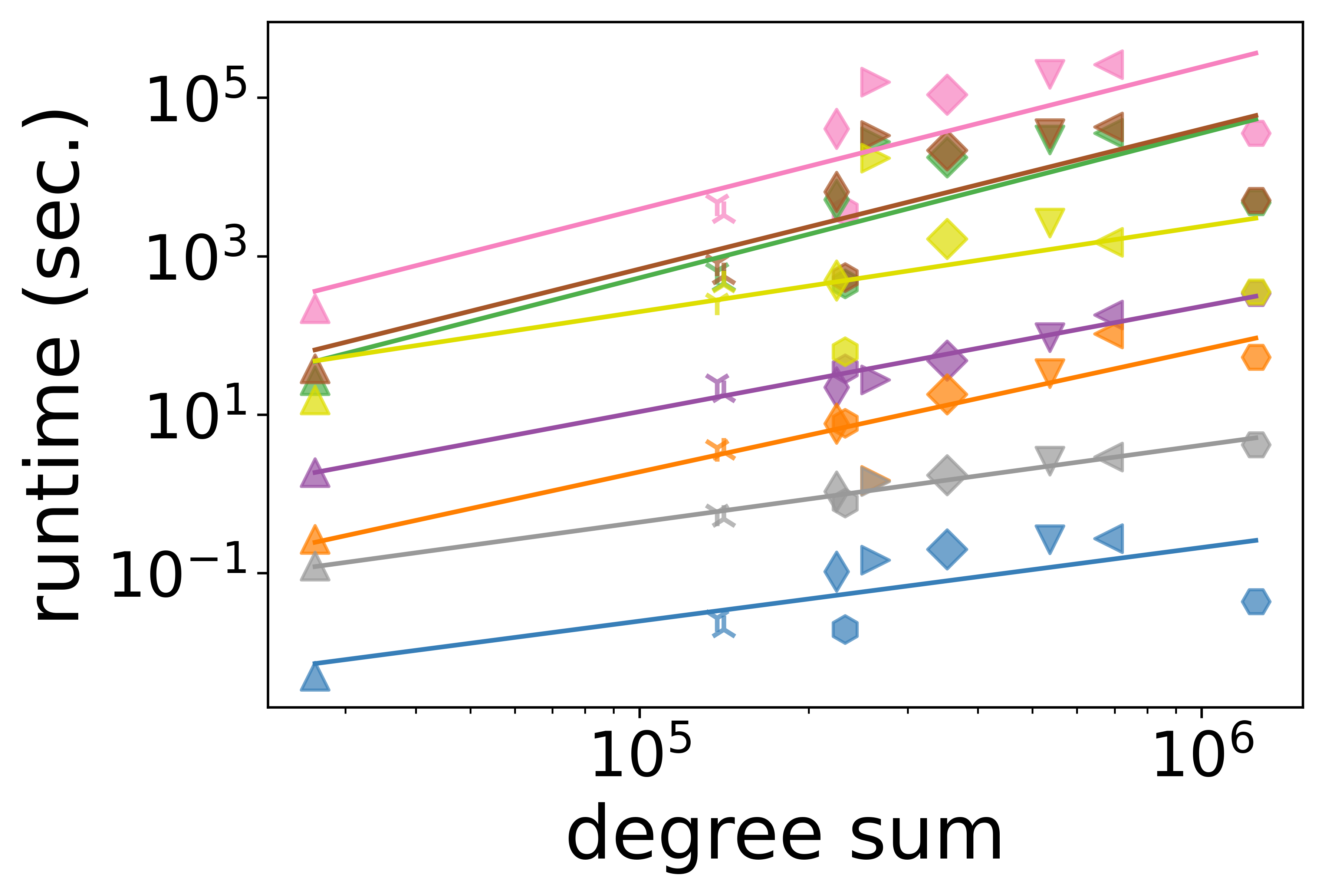
Figure 4: Scalability of node centrality measures as a function of node count, illustrating computational efficiency gaps.

The authors highlight that degree-based metrics can sometimes serve as reasonable proxies for more expensive measures when computational constraints are tight, but with potential tradeoffs in capturing structural nuance.

Applications and Practical Implications

The survey emphasizes the breadth of application domains:

• Social Systems: Hypercore-based measures effectively identify influential spreaders and group orchestrators, outperforming pairwise reductions in group-based information dynamics.
• Biological Networks: Betweenness and advanced spectral centralities locate critical genes, proteins, or multimorbidity clusters in high-order biological interaction contexts.
• Neuroscience: Hypergraph-based spectral measures reveal nontrivial functional hubs and resilience patterns in connectomic data, going beyond dyadic approximation.
• Infrastructure and Transport: Betweenness and other measures accurately pinpoint disruption-vulnerable hubs in settings with nonpairwise operational units.

The authors note a growing trend toward context-sensitive, learning-based, or task-optimized centrality scoring, especially in domains with rich side information.

Theoretical and Practical Outlook

The results challenge any notion of a universal or canonical centrality in hypergraphs. The diversity of definitions and their varying empirical behavior underscore the need to align measure selection with modeling assumptions, data availability, and computational constraints. Contradictory centrality rankings for key nodes and hyperedges across definitions underscore the necessity of methodological transparency and domain specificity.

The following open directions are proposed:

• Development of axiomatic frameworks for hypergraph centrality, mirroring mature treatments seen for pairwise networks.
• Unified meta-frameworks for the notion of path and distance in hypergraphs, potentially parametrizing over walk, path, and edge adjacency regimes.
• Native non-uniform spectral centrality operators, moving beyond reductionist transformations or auxiliary node injection.
• Robust and efficient approximation algorithms for computationally demanding measures, leveraging hardware acceleration and approximate inference.
• Standardized, large-scale benchmarking suites to facilitate cross-method comparison and establish practical best practices.

Conclusion

This survey provides a principled and comprehensive taxonomy of hypergraph centrality and importance measures, underpinned by a thorough empirical analysis. Strong numerical evidence demonstrates substantial structural and functional diversity among measures, with marked tradeoffs between interpretability, computational tractability, and expressiveness. The taxonomy and empirical insights equip researchers to make informed selections of centrality measures, motivate the development of new, context- and task-aware methods, and catalyze future theoretical and algorithmic advances in higher-order network science.