Recursive Clifford noise reduction (2511.22624v1)

Abstract: Clifford noise reduction (CliNR) is a partial error correction scheme that reduces the logical error rate of Clifford circuits at the cost of a modest qubit and gate overhead. The CliNR implementation of an $n$-qubit Clifford circuit of size $s$ achieves a vanishing logical error rate if $snp^2\rightarrow 0$ where $p$ is the physical error rate. Here, we propose a recursive version of CliNR that can reduce errors on larger circuits with a relatively small gate overhead. When $np \rightarrow 0$, the logical error rate can be vanishingly small. This implementation requires $\left(2\left\lceil \log(sp)\right\rceil+3\right)n+1$ qubits and at most $24 s \left\lceil(sp)^4\right\rceil $ gates. Using numerical simulations, we show that the recursive method can offer an advantage in a realistic near-term parameter regime. When circuit sizes are large enough, recursive CliNR can reach a lower logical error rate than the original CliNR with the same gate overhead. The results offer promise for reducing logical errors in large Clifford circuits with relatively small overheads.

• The paper introduces Recursive CliNR, a hierarchical sub-circuit strategy that overcomes error bottlenecks in Clifford circuits.
• It achieves polynomial suppression of logical errors as np tends to zero, independent of circuit size, with modest gate and qubit overheads.
• Quantitative analyses via Markov models and Monte Carlo simulations demonstrate significant performance gains over the standard CliNR protocol.

Recursive Clifford Noise Reduction: Error Mitigation Beyond Asymptotic Barriers

Introduction and Motivation

Practical quantum computing is constrained by physical error rates and limited qubit counts, impeding the deployment of full-scale fault-tolerant QEC. In this context, partial error mitigation protocols are of high relevance, especially for Clifford circuits, which underpin many quantum subroutines. The Clifford Noise Reduction (CliNR) protocol achieves polynomially suppressed logical error rates at modest qubit and gate overheads, but its efficacy is fundamentally limited by circuit size—the original CliNR only succeeds in the asymptotic regime $s n p^2 \to 0$, with $s$ the circuit size, $n$ qubits, and $p$ the physical gate error rate.

This paper introduces a recursive generalization of CliNR, termed Recursive CliNR, that employs a hierarchical sub-circuit approach. Recursive application overcomes the error bottleneck from single-level resource state injection (RSI), extending the regime of vanishing logical errors to $n p \to 0$, independent of $s$, for Clifford circuits of arbitrary size. Theoretical guarantees are complemented by quantitative simulation and Markov model analyses, substantiating the protocol's superior performance in near-term quantum hardware scenarios with realistic qubit counts and error rates.

Standard CliNR and Limitations

Standard CliNR consists of three sequential steps: resource state preparation (RSP), resource state verification (RSV) via random stabilizer measurements, and resource state injection (RSI) for logical circuit application. Each failing error detection in RSV leads to computational restarts, making the restart rate prohibitive for large $s$. Moreover, undetected errors during RSI accumulate without correction, resulting in logical error rates scaling unfavorably with circuit size.

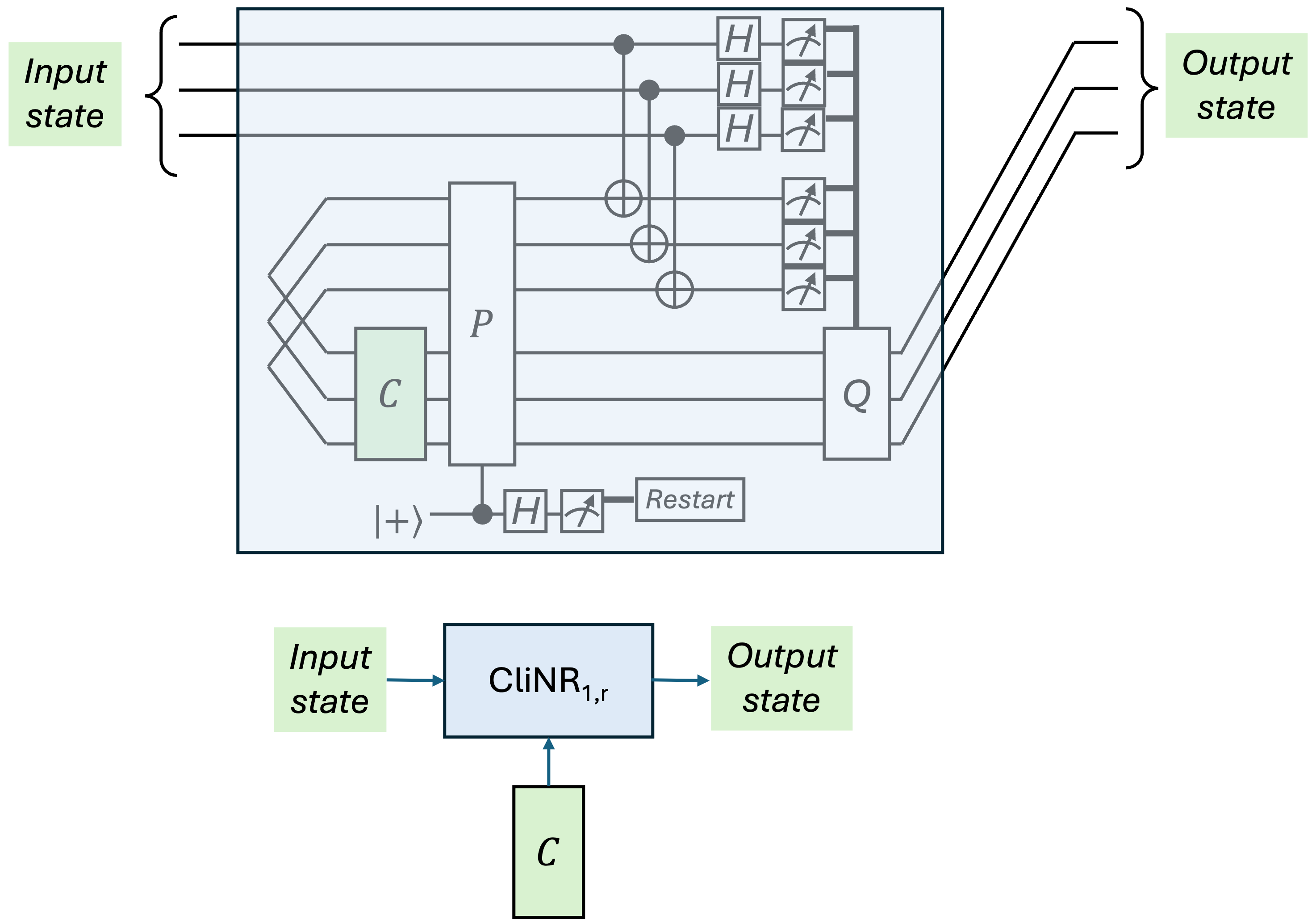
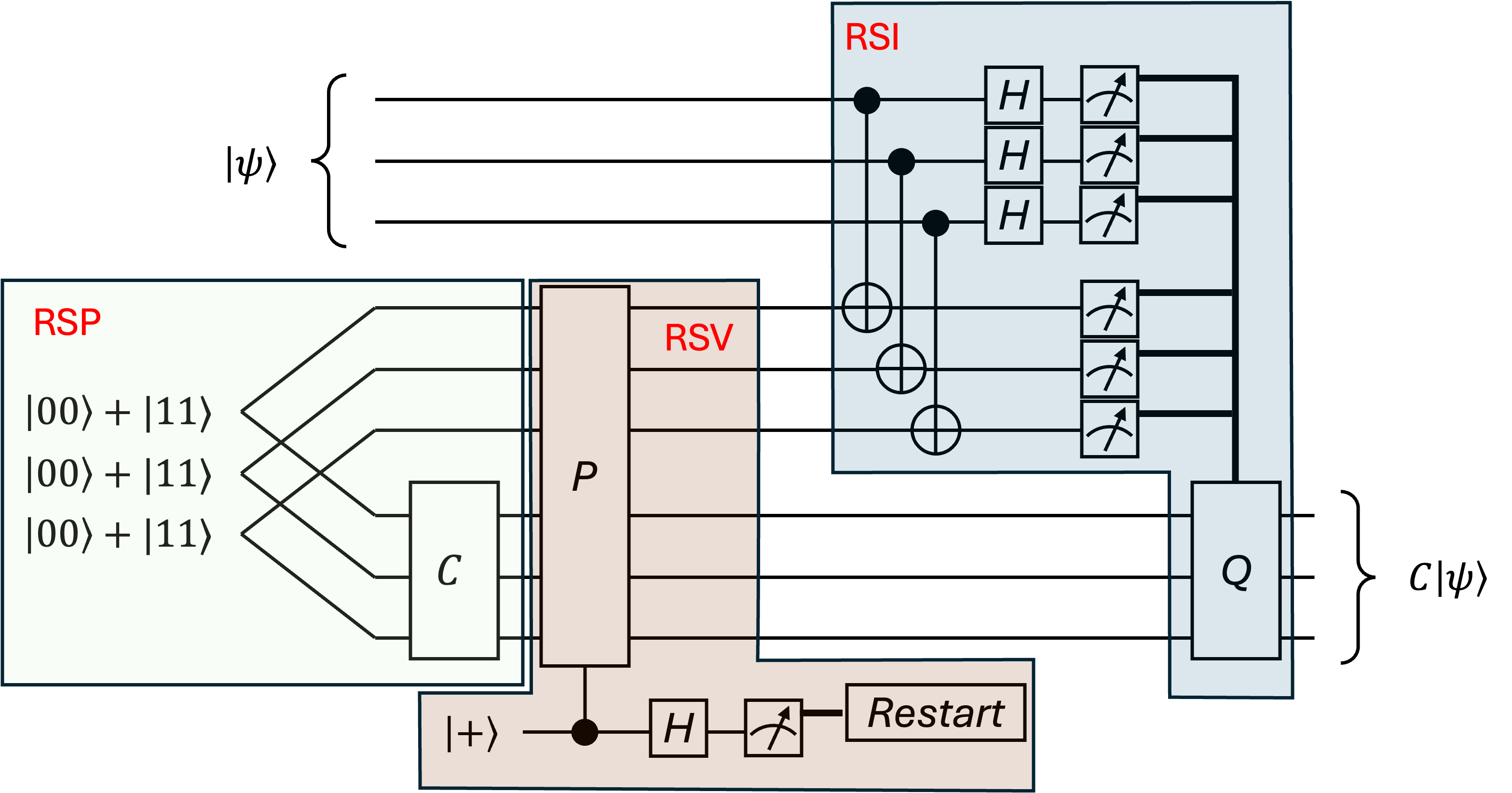
Figure 1: Schematic of the standard $\CliNR_1$ circuit, illustrating RSP, RSV, and RSI stages and their respective resource costs.

Recursive CliNR Protocol

Recursive CliNR replaces each target Clifford subcircuit of the main circuit with a recursively protected sub-protocol. The composition is strictly defined via a hierarchical CliNR tree: each tree node describes a subcircuit, its size, and the number of random stabilizer checks. RSI errors that elude direct detection in lower recursion levels are deferred to higher levels, where stronger verification is possible. This architecture enables error suppression beyond the limitations of direct or non-recursive error reduction.

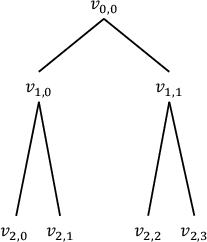
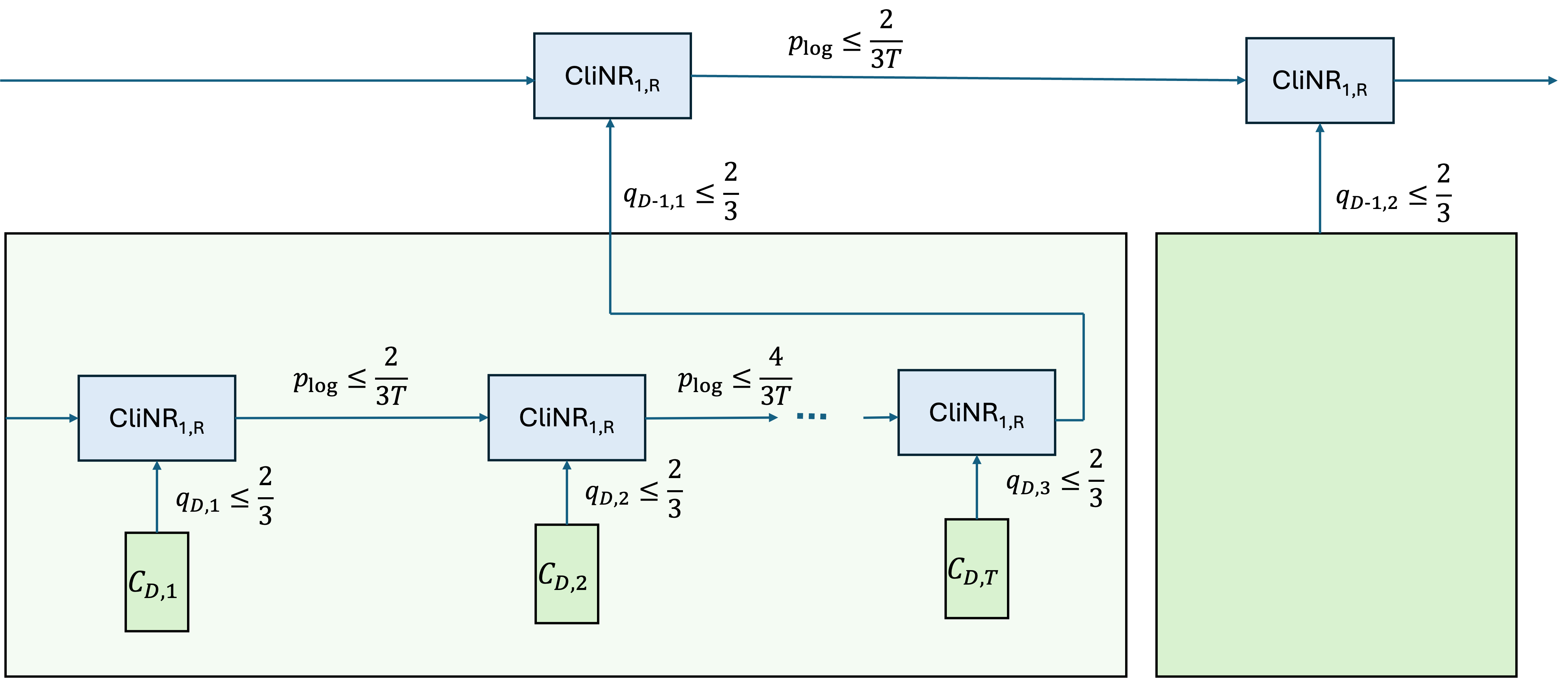
Figure 2: Example of a depth-2 Recursive CliNR tree, where every node is parameterized by the subcircuit size and the number of stabilizer checks.

Resource overheads are formalized: for a tree of depth $D$, Recursive CliNR requires $(2D+1)n+1$ physical qubits. The gate overhead remains weakly polynomial in $sp$. By uniformly bounding the error rates in subcircuits at each recursion level, the protocol ensures the overall logical error rate vanishes for $n p \rightarrow 0$, irrespective of the total circuit size.

Performance Analysis and Main Theorem

Theoretical guarantees for the recursive scheme are rigorously established via explicit bounds on logical error rate and gate overhead. The main theorem asserts:

For an $n$-qubit Clifford circuit of size $s$ with error rate $p$, Recursive CliNR attains vanishing logical error rate as $n p \rightarrow 0$ with gate overhead at most $24 s \lceil (sp)^4 \rceil$ and qubit overhead $(2 D + 1) n + 1$, where $D = \max\{1, \lceil \log_2(sp) \rceil + 1\}$.

Uniformly Bounded Implementation

A key contribution is the explicit construction of a uniformly bounded implementation. This algorithm assigns subcircuit sizes and the number of stabilizer checks such that, at any tree level, the subtree logical error rate is tightly bounded, ensuring overall polynomial resource costs.

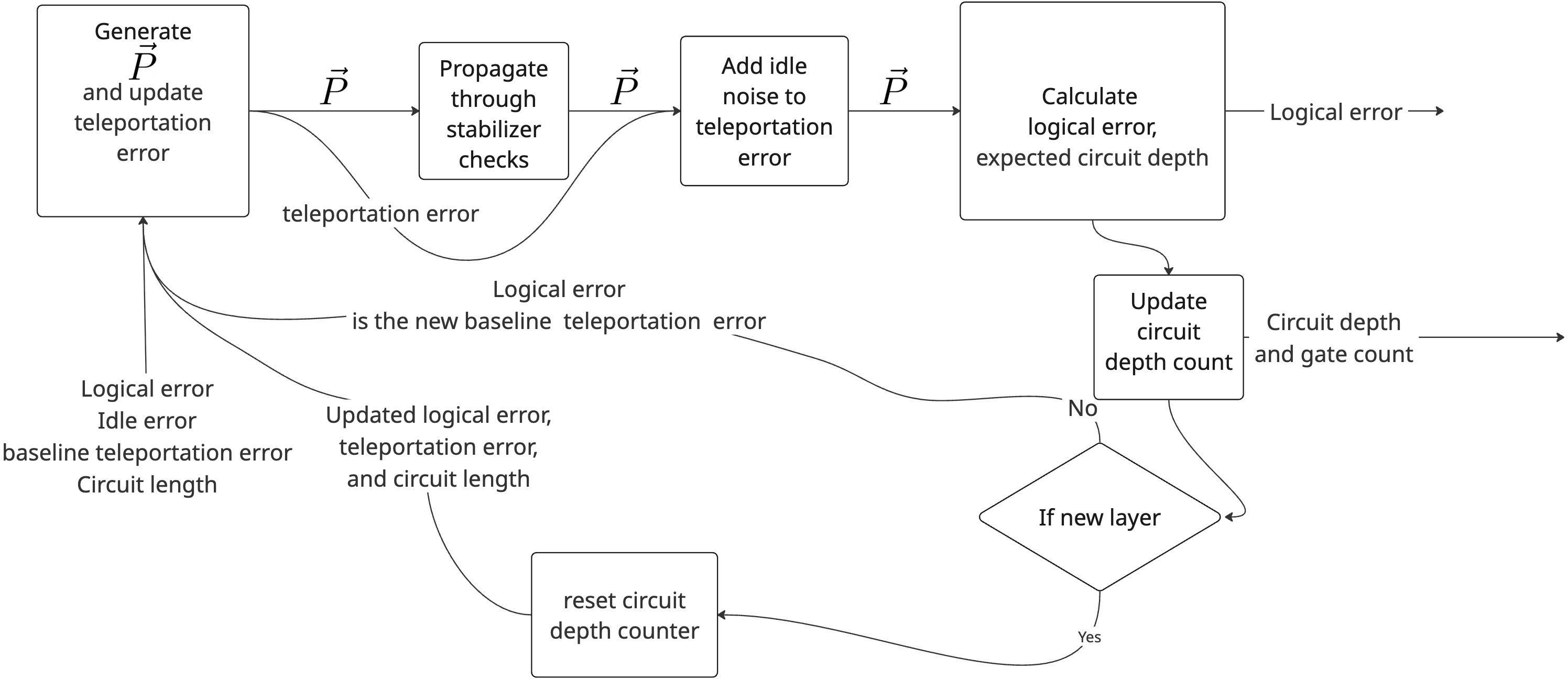
Figure 3: Markov model update and logical error estimation for composite recursive circuits, including stable tracking of error probabilities through circuit recursion.

Numerical and Simulation Results

Numerical estimates using a Markov model, alongside large-scale Monte Carlo simulations, showcase the practical advantage of Recursive CliNR. At $n=70$ and $p=10^{-3}$, recursive schemes begin to outperform the original for modest gate overheads, even in the presence of idle noise. For $n=400$ and $p=10^{-4}$, the recursive protocol delivers a logical error rate reduction from approximately $0.35$ to $0.10$ at comparable overhead.

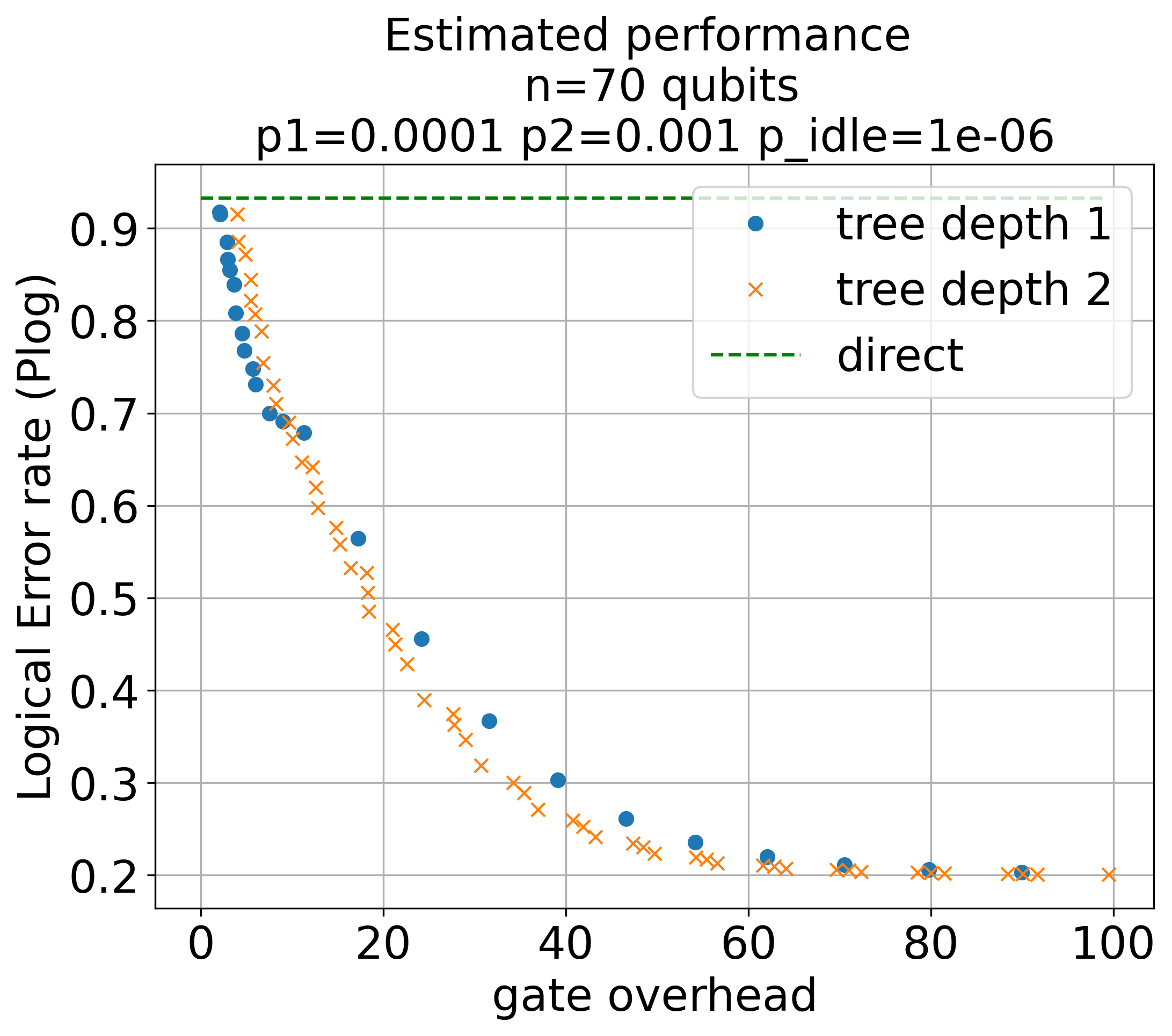
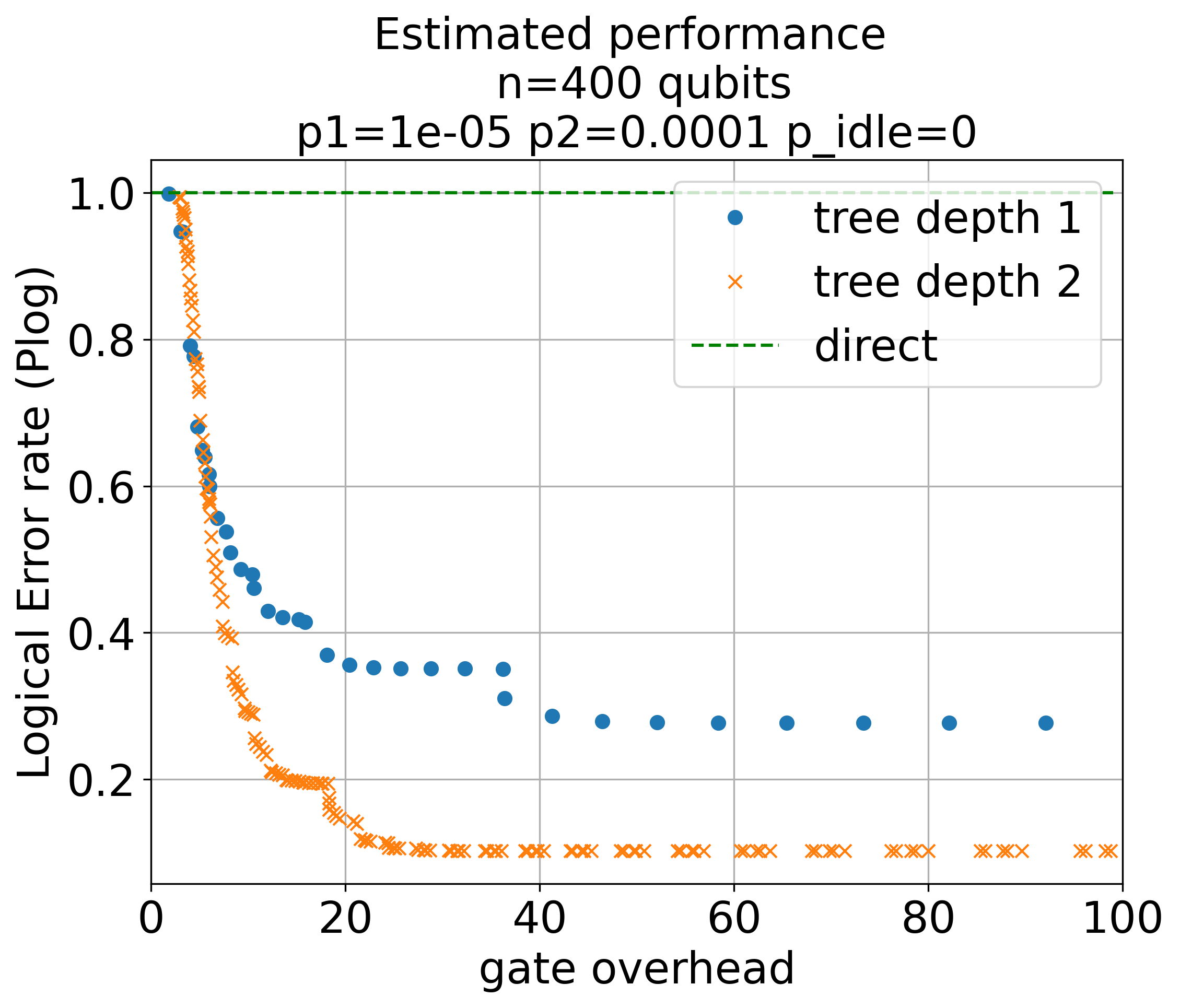
Figure 4: Markov model numerical estimates for error rate as a function of gate overhead for different recursion depths, demonstrating the suppression crossover.

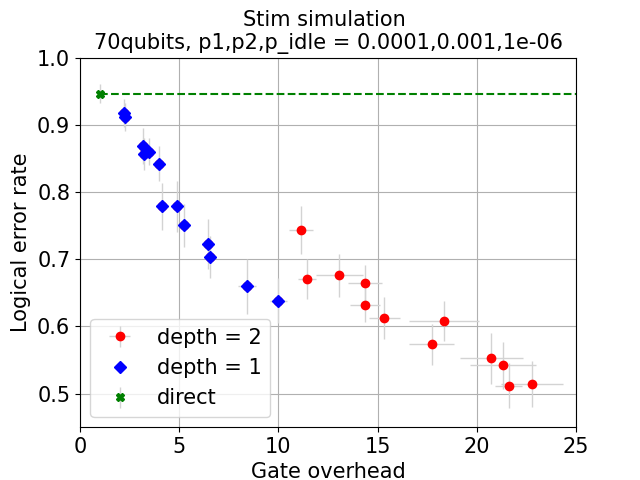
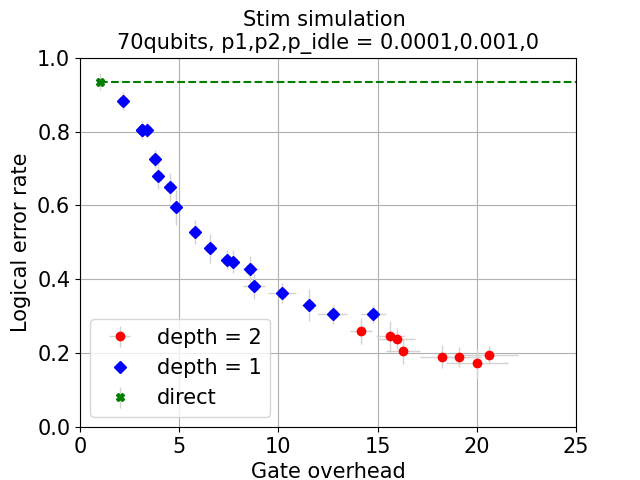
Figure 5: Stim-based stabilizer Monte Carlo simulations of logical error rates for Recursive CliNR versus original CliNR under idle and non-idle noise settings.

Systematic parameter optimization via the Markov approach enables practical tree selection for hardware-traceable deployments. Recursive CliNR's benefit is maximized in circuits with low idle error and scalable qubit counts, such as in ion-trap hardware platforms.

Implications and Future Directions

The practical implication is that Recursive CliNR allows for deep Clifford computation with modest hardware resources, filling the performance gap until fully fault-tolerant QEC becomes viable. Theoretically, this relaxes the circuit size constraints for error mitigation from $s n p^2 \to 0$ to the far milder $n p \to 0$, a substantial extension of the domain of utility-scale quantum computation.

There are immediate avenues for enhancement:

• Parallelization: If further qubits are available, parallel RSI and RSV at the same recursion depth reduce idle-induced errors and runtime latency.
• Stabilizer Selection Optimization: Algorithmic selection of stabilizer generators for RSV can tighten error suppression and minimize overhead, as shown in related literature.
• Hybridization with Full QEC: In the long term, recursive error mitigation may operate synergistically with topological codes, providing "soft" fault-tolerance layers for Clifford-dominated workloads.

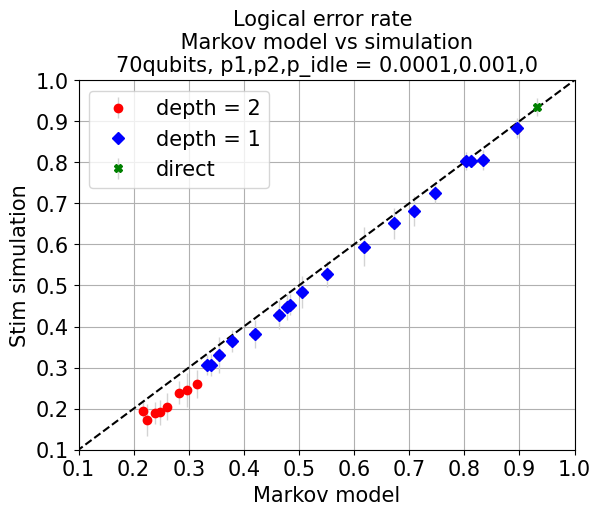
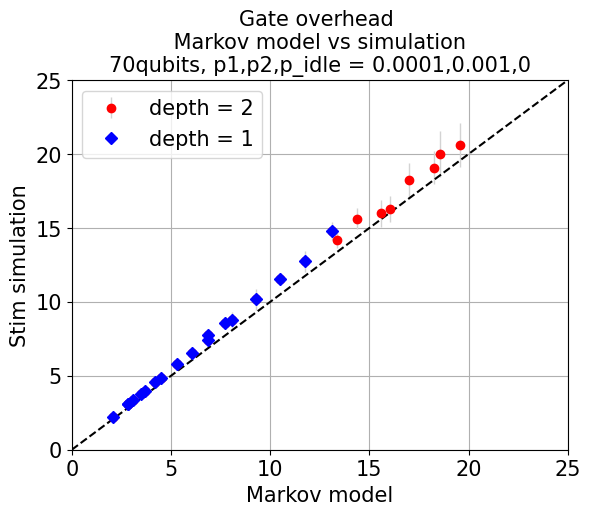
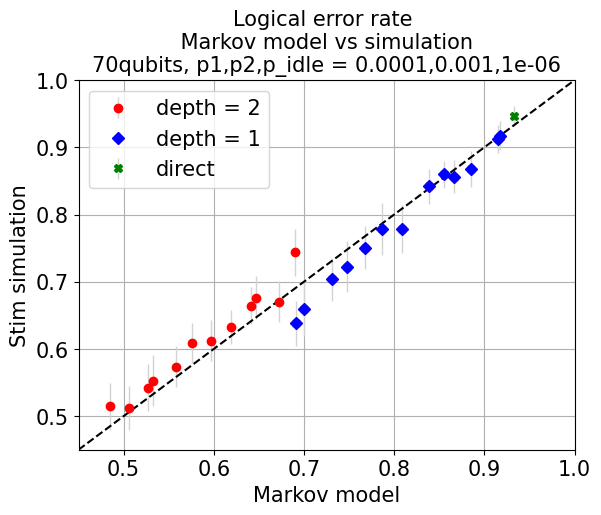
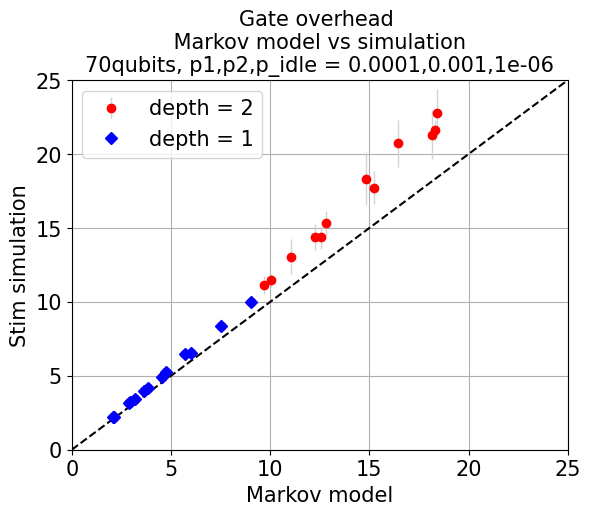
Figure 6: Comparison of Markov model predictions with Monte Carlo simulation, establishing the validity of the analytic model for tree selection and performance estimation.

Conclusion

Recursive CliNR represents a formal advance in quantum error mitigation for Clifford circuits by pushing the threshold for utility-scale, non-fault-tolerant quantum computation. The protocol both deepens the theoretical understanding of sub-QEC error reduction and delivers immediate practical gains for near-term devices, particularly in platforms capable of large qubit counts and low idle error rates. The framework is sufficiently general to motivate future hybrid schemes and parallel constructions, extending its utility as full-scale quantum architectures mature.