Possibilistic Instrumental Variable Regression (2511.16029v1)
Abstract: Instrumental variable regression is a common approach for causal inference in the presence of unobserved confounding. However, identifying valid instruments is often difficult in practice. In this paper, we propose a novel method based on possibility theory that performs posterior inference on the treatment effect, conditional on a user-specified set of potential violations of the exogeneity assumption. Our method can provide informative results even when only a single, potentially invalid, instrument is available, offering a natural and principled framework for sensitivity analysis. Simulation experiments and a real-data application indicate strong performance of the proposed approach.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What this paper is about
This paper introduces a new way to paper cause-and-effect relationships when the usual “helper variables” (called instrumental variables, or IVs) might not be perfectly trustworthy. Instead of using standard probabilities, the authors use “possibility theory” to judge how plausible different answers are. Their method can still give useful results even if you only have one instrument that might be flawed, and it’s designed to be a clear, principled way to do sensitivity analysis (checking how conclusions change when assumptions are relaxed).
The main idea and questions
The paper focuses on instrumental variables, which are extra pieces of information used to fix hidden biases in cause-and-effect studies. For an IV to be valid, it should:
- Be related to the treatment (relevance).
- Be free from hidden confounders (exogeneity).
- Affect the outcome only through the treatment, not directly (no direct effect).
In real life, these conditions can be hard to guarantee. The authors ask:
- How can we estimate a treatment’s causal effect when instruments might slightly break the rules (especially by having a small direct effect on the outcome)?
- Can we do this in a way that clearly reflects our uncertainty without inventing extra assumptions?
- Can the method work even with just one possibly invalid instrument?
- Can we provide uncertainty intervals that are trustworthy (well-calibrated) while doing sensitivity analysis?
How the method works (in everyday language)
Think of the analysis like a detective story:
- You want to know if the treatment X causes changes in outcome Y (for example, does a medicine improve health?).
- You have instruments Z (like a hospital policy) that help tease apart cause from correlation. But you’re not 100% sure Z is perfectly clean—it might affect Y a tiny bit on its own.
The standard approach assumes the instrument affects Y only through X (no direct effect). This paper relaxes that: it lets the instrument have a small direct effect on Y, but only within a user-chosen “allowed range” A (your tolerated amount of rule-breaking).
Here’s the approach in simple steps:
- Step 1: Fit a simple “reduced-form” model that directly relates both Y and X to the instruments Z. This is like summarizing the evidence without deciding yet what caused what.
- Step 2: Translate those summaries into the “structural” cause-and-effect quantities you care about (the treatment effect β and the instrument’s direct effect α). When instruments might be slightly invalid, this translation is not unique.
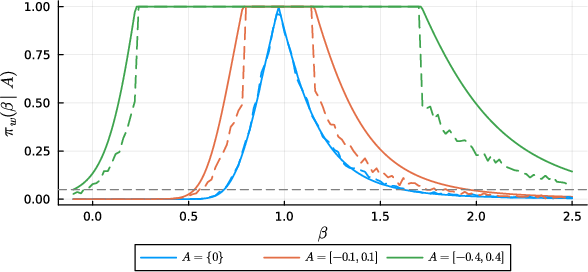
- Step 3: Use possibility theory to pick the “most possible” values consistent with the data and your allowed violation set A. Instead of averaging over all possibilities (probabilities integrate), possibility theory looks for the highest-supported (most plausible) values.
- Step 4: Compute how possible each value of β is, given that α must lie in A. If the best-fitting α for a given β stays inside A, that β is fully plausible; if it falls outside, the method projects α back onto A and down-weights how possible that β is.
- Step 5: “Validify” the results. The authors apply a calibration procedure so that the resulting intervals for β have controlled error rates—meaning they won’t reject the true effect too often, as long as the true α lies inside the set A you chose.
Two practical ways to compute these “validified” possibilities:
- Monte Carlo sampling (simulate many datasets to approximate the calibration).
- A faster chi-square approximation (good when samples are larger).
What they found and why it matters
The authors run two kinds of tests: computer simulations and a real-world economic example.
- Simulations (single instrument and multiple instruments):
- If you assume perfect instruments when they are actually slightly invalid, standard methods like two-stage least squares (TSLS) can give intervals that miss the truth too often.
- The possibilistic method gives intervals that stay well-calibrated if your allowed violation set A includes the true amount of invalidity (your tolerance matches reality). If A is too wide, intervals get very conservative (too large), but they remain safe.
- It works even with only one possibly invalid instrument—something many other methods struggle with.
- Compared to other approaches (like BudgetIV or plausible GMM), their method often strikes a better balance: not too narrow (overconfident), not too wide (overly cautious), and always available even when other methods fail to return a sensible set.
- Real data (institutions and economic growth):
- The classic question: Do better institutions (like protection against expropriation) raise a country’s income?
- The instrument is historical settler mortality. It might not be perfectly valid, so they allow small violations (e.g., α within [-0.1, 0.1]).
- Result: Even after allowing for small invalidity, the estimated effect remains clearly positive. If you allow very large violations (e.g., α up to ±0.4), the strong conclusion can weaken—exactly what sensitivity analysis is supposed to show.
Why this is important:
- It turns uncertainty about instrument validity into a transparent input (the set A), and it gives you intervals that honestly reflect that uncertainty.
- It supports careful sensitivity analysis—how far can you relax the assumptions before your conclusion changes?
What this could change going forward
- Better sensitivity analysis: Researchers can say, “Our conclusion holds as long as the instrument’s direct effect is within this range.”
- Works with few instruments: Even a single, possibly imperfect instrument can be used in a principled way.
- Honest uncertainty: The method emphasizes interval estimates (ranges of plausible effects) instead of single numbers, which is often more realistic when assumptions are shaky.
- Trade-off you control: You choose the violation set A. If A is too large, results get less informative; if it’s too small and misses the truth, you risk undercoverage. Domain knowledge should guide this choice.
In short, the paper offers a clear, robust, and practical framework for causal inference when instrument validity is uncertain—making it easier to trust the conclusions and to understand exactly how much assumption-breaking they can withstand.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of gaps and open questions that remain unresolved and could guide future research.
- Formal elicitation of the violation set A: Develop principled, reproducible procedures to translate domain knowledge into a specific constraint set (e.g., via negative controls, prior-to-possibility mapping, expert elicitation protocols, or calibration using auxiliary data), including guidance on scale and units after standardizing instruments.
- Sensitivity to misspecification of A: Characterize how inference (coverage, Type I/II errors, set width) degrades when the true , and propose robustifications (e.g., union-of-sets, adaptive enlargement rules, conservative envelopes) that retain validity under partial misspecification.
- Asymptotic theory for validification: Provide rigorous conditions under which the Wilks-style approximation to is accurate (including weak-instrument regimes), and specify its finite-sample error rates relative to Monte Carlo validification.
- Weak instruments: Analyze the behavior of the validified posterior possibility and confidence sets when instrument relevance is weak (small ), including diagnostics, recommended adjustments (e.g., informative possibilistic priors), and theoretical bounds on interval growth.
- High-dimensional instruments (): Extend the method when is singular (many instruments), including regularized possibilistic priors, computational strategies, and theoretical guarantees (existence, stability, and validity of and the projection onto ).
- Error structure and robustness: Generalize beyond joint Gaussian errors to heteroskedastic, clustered, autocorrelated, or heavy-tailed disturbances; develop robust/“sandwich” variants and establish validification results under such misspecification.
- Nonlinear and discrete outcomes/treatments: Adapt the framework to generalized linear models (binary or count ), limited dependent variables, and nonlinear first-stage/outcome relations, including appropriate reduced-form mappings and validification.
- Multiple endogenous regressors: Extend the structural mapping () and inference to vector-valued treatments and multi-equation systems, with corresponding identification and validification theory.
- Choice of projection metric: Justify or optimize the use of the -induced metric for ; compare alternatives (e.g., Mahalanobis metrics using instrument covariance or ) and quantify their impact on inference.
- Computational scalability: Improve the efficiency of validification (currently Monte Carlo or approximation), e.g., via importance sampling, parametric bootstrap pivots, or reuse of simulation across grids, with complexity guarantees for large .
- Possibilistic priors beyond vacuous: Design and paper sparsity- or structure-inducing possibilistic priors on (e.g., balls, group budgets) and quantify how they affect -inference and validity, especially under many/weak instruments.
- Joint inference for : Develop methods to infer (and instrument validity) jointly with under the possibilistic framework, beyond conditioning on , while retaining strong validity guarantees.
- Efficiency and power: Derive theoretical bounds or optimality criteria for expected length and power of as functions of , , and instrument strength; propose procedures to choose that balance validity and efficiency.
- Outliers and leverage: Assess robustness to high-leverage points and outliers in and ; propose robust possibilistic IV variants (e.g., M-estimation-based reduced-form) and evaluate their validification.
- Practical sensitivity algorithms: Provide algorithms to compute the minimal violation budget (e.g., in ) at which a target claim (e.g., ) ceases to hold at level , with uncertainty quantification.
- Invariance and reparameterization: Examine invariance properties of the possibilistic posterior under reparameterizations (given the no-Jacobian feature), and clarify any consequences for interpretability and scale dependence when instruments are not standardized.
- Combining multiple datasets: Develop principled rules for possibilistic updating and evidence synthesis across studies (outer-measure combination), addressing non-additivity and ensuring validified inference under pooled information.
- Presentation of multi-modal/partial-identification sets: Provide guidance and tooling to summarize and visualize non-unique modes and potentially disjoint confidence regions in , including decision-theoretic interpretations under upper/lower probabilities.
- Empirical benchmarking: Systematically compare against partial identification methods (e.g., Conley bounds, BudgetIV), across a wide grid of instrument strengths, invalidity patterns, and shapes, focusing on coverage-precision trade-offs and computational costs.
- Shapes of A beyond hypercubes and norm-balls: Develop efficient projection routines and closed-form results for structured (sign constraints, group budgets, polyhedral sets), and paper how geometry of maps into the partial identification region for .
- Nuisance parameter handling in validification: Clarify how sampling from in practice uses plug-in estimates (e.g., ), and analyze the induced error on ; propose corrected or double-bootstrap schemes with theoretical guarantees.
- Real-data generalization: Extend the AJR application to multiple instruments and alternative specifications (e.g., clustered errors, additional controls), and test sensitivity to different calibrations, instrument transformations, and standardization choices.
Glossary
- Affine subspace: A flat, translated linear subspace; here, the locus of α implied by a given β in the reduced-form relation. "the affine subspace $t(\beta) = \Hat{\gamma}_1 - \beta \Hat{\gamma}_2$"
- Aleatoric uncertainty: Uncertainty due to inherent randomness in outcomes; contrasted with deterministic unknowns. "thus there is no aleatoric uncertainty connected to $\Omega_{\mathrm{u}$."
- BudgetIV: A partial-identification method that constrains instrument invalidity by a budget on direct effects. "BudgetIV can similarly maintain good coverage, as it also relies on partial identification"
- CIIV: Confidence interval method for IV that uses searching/voting to recover valid instruments. "Now, we also include the confidence interval method (CIIV) \citep{windmeijer_confidence_2021}"
- Conditional outer measure: A possibilistic analogue of conditional probability, defined via suprema rather than integrals. "Conditional outer measures can be defined analogously to probability theory as"
- Endogeneity: Correlation between regressors and error terms that biases naive outcome regression. "Whenever is not diagonal, this indicates unobserved confounding (or endogeneity)"
- Endogenous variable: A regressor whose value is correlated with unobserved disturbances in the outcome equation. "a treatment or endogenous variable"
- Epistemic uncertainty: Uncertainty due to lack of knowledge about parameters, not randomness. "as the widened intervals arise directly from epistemic uncertainty about the parameters rather than from ad-hoc adjustments"
- Exogeneity: Assumption that instruments are uncorrelated with unobserved confounders and affect outcome only through treatment. "Assumptions A2 and A3 are typically grouped together and referred to as exogeneity or validity of the instruments"
- Exogeneity assumption: The requirement that instruments be valid (unconfounded and exclusion restriction holds). "violations of the exogeneity assumption"
- Exogenous covariates: Observed control variables assumed uncorrelated with the structural errors. "we do not explicitly account for exogenous covariates, but these can be easily considered"
- First-stage R2: The proportion of variance in the treatment explained by instruments in the first-stage regression. "which corresponds to a first-stage of approximately $1/4$"
- gIVBMA: Bayesian model averaging over instrument sets in IV settings. "Now, we also include the confidence interval method (CIIV) \citep{windmeijer_confidence_2021} and gIVBMA \citep{steiner_bayesian_2025}."
- Identification: The property that structural parameters are uniquely determined by the observable reduced-form parameters. "The structural parameters are identifiable if we can find a unique solution given "
- Instrumental variables (IVs): Variables that affect treatment, are unconfounded, and influence outcome only through treatment. "Instrumental variables (IVs) offer an approach to estimating treatment effects in the presence of unobserved confounding."
- Jacobian term: Determinant factor in change-of-variables formulas in probability; absent in possibilistic transforms. "There is no need to account for the change in measure by a Jacobian term."
- Joint possibility function: A function assigning degrees of possibility to pairs of uncertain variables, analogous to joint densities. "where $f_{\bo\theta, \bo\psi}$ is a joint possibility function."
- ℓ1-penalisation: Regularisation using the L1 norm to select or shrink invalid instruments. "Estimation in this setting typically relies on -penalisation"
- Matrix Gaussian prior: A prior over matrices with Gaussian structure, here aligned with the column covariance. "a possibilistic Matrix Gaussian prior on with column covariance "
- Matrix Normal distribution: A distribution for matrices with separable row/column covariance structure. "follows a matrix Normal distribution, "
- Moment restrictions: Conditions that certain expectations (moments) equal zero, defining structural models in GMM. "a structural model characterized by a set of moment restrictions"
- Monte Carlo approximation: Numerical estimation via random sampling, used to approximate validified possibility. "A natural Monte Carlo approximation is"
- Orthogonal (direct effects): Assumption that direct effects on outcome and treatment are uncorrelated. "assume that the direct effects on the outcome and the treatment are orthogonal"
- Outer measure: A non-additive measure providing an upper bound on probabilities in possibilistic inference. "the outer measure can be seen as an upper bound on probability measures."
- Outer probability measure: Supremum-based measure over sets derived from a possibility function. "This possibility function gives rise to an outer probability measure"
- Overidentifying restrictions: Extra moment conditions available when instruments exceed endogenous regressors. "focus only on misspecification of overidentifying restrictions"
- Partial identification: Situation where parameters are set-identified rather than point-identified given the data and assumptions. "The literature on partial identification in instrumental variable models is closely related"
- PGMM-g: Plausible generalized method of moments with a Gaussian prior over violations. "plausible generalised method of moments with a Gaussian prior (PGMM-g) \citep{chernozhukov_plausible_2025}"
- Plurality rule: Identification strategy assuming fewer than half of instruments are invalid. "Under the plurality rule, the treatment effect can be identified without knowing in advance which instruments are valid"
- Positive-semidefinite cone: The set of symmetric matrices with nonnegative eigenvalues; a convex cone. "where is the cone of positive-semidefinite and symmetric matrices."
- Possibility function: A mapping from parameter values to [0,1] indicating degrees of plausibility, peaking at 1. "We characterise the uncertain variable $\bo{\theta}$ by a possibility function $f_{\bo{\theta} : \Theta \to [0, 1]$"
- Possibility theory: A framework for uncertainty using possibility/necessity rather than probability. "Based on possibility theory \citep{zadeh_fuzzy_1999, dubois_possibility_2015}, our proposed approach can still perform inference"
- Posterior possibility function: The possibilistic analogue of a posterior, proportional to likelihood times prior possibility with sup-normalization. "Then, the posterior possibility function is"
- Projection (onto A with respect to ): Minimizing distance to A under the metric induced by the instrument matrix. "denotes the projection onto with respect to the metric induced by ."
- Quadratic programming problem: Optimization of a quadratic objective under linear constraints, used for projections onto rectangles. "computing the projection is a standard quadratic programming problem."
- Quasi-Bayesian: Approaches that adopt Bayesian-like updating without full probabilistic priors over all model components. "develop a quasi-Bayesian framework to allow for the possibility that all restrictions are invalid."
- Reduced-form model: Statistical model of observed variables (outcome/treatment) as a function of instruments without structural decomposition. "Consider the “reduced-form” equation model"
- Reduced-form parameters: Parameters of the observable model (e.g., γ1, γ2, Ψ) prior to mapping back to structural parameters. "no one-to-one correspondence between the (always identifiable) reduced-form parameters and the structural parameters"
- Relevance: The requirement that instruments affect the treatment (nonzero first-stage coefficient). "A1 is known as relevance."
- Sensitivity analysis: Assessing robustness of causal conclusions under controlled violations of assumptions. "The main use case we envision for our method is sensitivity analysis."
- Structural parameters: Parameters of the causal model (e.g., β, α, Σ) describing relationships and error covariances. "The structural parameters are identifiable if we can find a unique solution "
- Strong validity: Property that the validified possibility controls type-I error at the nominal level uniformly. "is strongly valid in the sense that for any "
- TSLS (Two-stage least squares): Classical IV estimator performing first-stage prediction then second-stage outcome regression. "naive two-stage least squares (TSLS)"
- Type-I error: Probability of incorrectly rejecting a true hypothesis; controlled by validification. "the validified posterior possibility controls the type-I error"
- Type-II error: Probability of failing to reject a false hypothesis; inversely related to the tightness of violation set A. "minimise the type-II error), which is inversely proportional to the volume of ."
- Uncertain variable: A deterministic-but-unknown quantity modeled in possibilistic terms via a possibility function. "An uncertain variable $\bo{\theta}$ is a mapping from $\Omega_{\mathrm{u} \to \Theta$"
- Unobserved confounding: Hidden factors affecting both treatment and outcome, biasing naive estimates. "Instrumental variable regression is a common approach for causal inference in the presence of unobserved confounding."
- Vacuous prior information: An uninformative prior possibility assigning full credibility to all values (f = 1). "We focus on the case with vacuous prior information, i.e., ."
- Valid confidence set: A set with guaranteed coverage probability at or above the nominal level under specified assumptions. "the upper level sets are valid confidence sets."
- Validification: A transformation of posterior possibility to improve frequentist calibration via probability of being no larger than observed. "the validification procedure proposed by \cite{martin_inferential_2013}"
- Validified posterior possibility function: The calibrated possibility function obtained via the validification mapping. "the validified posterior possibility function"
- Violation set: A user-specified set of admissible instrument direct effects (α) against which β is conditioned. "Let be the considered violation set."
- Wilk's style χ2 approximation: Large-sample approximation that maps a likelihood-ratio-like statistic to a χ2 distribution. "the Wilk's style approximation"
Practical Applications
Practical, Real-World Applications of “Possibilistic Instrumental Variable Regression”
Below are actionable applications derived from the paper’s findings, methods, and innovations. Each item highlights the sector, potential tools/products/workflows, and key assumptions or dependencies that affect feasibility.
Immediate Applications
- Robust sensitivity analysis for existing IV studies (academia; economics, epidemiology, social sciences)
- Use when instrument exogeneity is uncertain to produce validified interval estimates that explicitly reflect tolerated violations A.
- Tools/workflows: R/Python/Stata module “Possibilistic IV” that (i) takes reduced-form estimates, (ii) asks users to specify A (e.g., hypercube or norm budget), (iii) returns validified posterior possibility and confidence sets via χ² or Monte Carlo approximation.
- Assumptions/dependencies: Linear IV model; Gaussian errors; i.i.d. sampling; validification guarantees require that the true α lies in the chosen set A; sufficient instrument relevance.
- Single-instrument fallback inference when the only instrument may be invalid (academia, policy evaluation; economics, public policy)
- Use to avoid discarding studies with a single, questionable instrument—recover interval-based inference rather than point estimates.
- Tools/workflows: “Single-IV mode” in econometrics software; standardized reporting template emphasizing partial identification regions.
- Assumptions/dependencies: Sensitivity hinges on a meaningfully bounded A; intervals can be wide if A is large.
- Policy-grade sensitivity reporting for program evaluation (policy; education, labor, taxation)
- Include possibilistic intervals in policy briefs to show how conclusions change as A widens (e.g., how much instrument invalidity would be needed to overturn a finding).
- Tools/workflows: Interactive dashboard with an “invalidity slider” for A; pre-registration of A choices; automatic generation of validified confidence sets.
- Assumptions/dependencies: Domain knowledge to set plausible A; transparency on instrument relevance and data preprocessing.
- Credible IV in observational healthcare studies (industry, academia; healthcare, pharmacoepidemiology)
- Apply to physician-preference, regional variation, or calendar timing instruments where exogeneity may be imperfect.
- Tools/workflows: EHR analytics workflow adding a “Possibilistic IV sensitivity block” alongside TSLS; output includes lower/upper probabilities for clinical hypotheses (e.g., β > 0).
- Assumptions/dependencies: Correct specification of linear relationships; adequate sample size for MC approximation or χ² validity; instrument standardization to interpret A.
- Mendelian Randomization robustness checks (academia; genetics/biostatistics)
- Use A to encode tolerated pleiotropy (direct effects of SNPs), yielding partial-identification-aware intervals complementary to MR-Egger and robust MR methods.
- Tools/workflows: Add-on to MR packages to project t(β) onto A; report validified posterior possibilities.
- Assumptions/dependencies: Linear approximations between genetic instruments and traits; careful calibration of A to reflect biological plausibility.
- Marketing and growth experimentation with imperfect instruments (industry; tech, e-commerce, advertising)
- Instruments like ad-budget shocks or platform algorithm changes may have direct effects on outcomes; use possibilistic IV to quantify robustness of lift estimates.
- Tools/workflows: Internal analytics pipeline with instrument standardization, selection of A via business constraints, and MC-based validification; “report generator” for leadership.
- Assumptions/dependencies: Relevance of instruments; availability of reduced-form estimates; willingness to accept interval conclusions.
- Energy and climate policy impact studies (policy, industry; energy economics)
- Instruments such as grid proximity or legacy subsidy eligibility can be partially invalid; possibilistic intervals offer defensible sensitivity ranges for emissions or adoption impacts.
- Tools/workflows: GIS-linked econometrics pipeline with A tied to standardized instrument scales; policy-facing visualizations of confidence sets.
- Assumptions/dependencies: Spatial correlation addressed via exogenous controls; validification requires α ∈ A.
- Finance: asset-pricing and market-microstructure analyses with questionable instruments (industry; finance)
- Use for instruments like index membership changes or regulatory thresholds that may have direct price effects.
- Tools/workflows: Research platform module producing validified possibilistic intervals; risk committee reports showing how conclusions vary with A.
- Assumptions/dependencies: Linear structure; stationary sampling; thorough exogenous covariate projection.
- Data journalism and public-facing analytics (daily life, media; education/communication)
- Communicate robustness of causal claims with interactive visuals of “possibility curves” and confidence sets as A varies.
- Tools/workflows: Web widgets implementing χ² approximation for speed and MC for accuracy; guidance on interpreting partial identification regions.
- Assumptions/dependencies: Simplified linear models; clear explanation of A to non-technical audiences.
- Auditable, first-principles uncertainty accounting in research pipelines (academia, industry; software/analytics)
- Replace ad-hoc “widened intervals” with principled possibilistic posteriors that are optimization-based and avoid improper priors.
- Tools/workflows: Library functions for projection onto A using ZᵀZ metric; standardized instrument preprocessing and reporting.
- Assumptions/dependencies: Correct implementation of projection; computational cost for MC validification in small samples.
Long-Term Applications
- Standardization of sensitivity-analysis reporting in journals and agencies (academia, policy; cross-sector)
- Establish guidelines that require possibilistic IV intervals with declared A, validification methods, and partial identification reporting.
- Tools/products: “Policy-grade Sensitivity Standard” and templates; journal checklists and automated compliance validators.
- Assumptions/dependencies: Community consensus on acceptable A ranges; training for analysts.
- Integrated econometrics platform for automated A-selection (software; economics, healthcare, finance)
- Recommend A based on domain priors, instrument diagnostics, and standardized scales; perform grid search over A to identify thresholds where conclusions change.
- Tools/products: “A-Calibrator” leveraging expert inputs, historical studies, and instrument relevance metrics.
- Assumptions/dependencies: Robust heuristics for A selection; careful avoidance of data snooping.
- Extension to non-linear and non-Gaussian IV models (academia; machine learning, advanced econometrics)
- Develop possibilistic inference for generalized linear models, binary outcomes, and heterogeneous treatment effects.
- Tools/products: Generalized Possibilistic IV library with validification under outer measures beyond Gaussian assumptions.
- Assumptions/dependencies: New theory for validification in non-Gaussian settings; computational scalability.
- High-dimensional and weak-instrument regimes (academia, industry; genetics, text/ad analytics)
- Combine possibilistic priors with regularization (e.g., Matrix Gaussian possibilistic priors) for many weak instruments.
- Tools/products: Penalized Possibilistic IV toolkit; hybrid workflows that blend ℓ₁ strategies with partial-identification-aware intervals.
- Assumptions/dependencies: Proper prior design to avoid inducing unintended priors on β; stability of optimization.
- Time-series and panel-data extensions (academia, policy; macroeconomics, operations)
- Possibilistic IV with dynamic instruments and autocorrelated errors; validified intervals for policy shocks over time.
- Tools/products: Panel Possibilistic IV module with clustered standardization and rolling validification.
- Assumptions/dependencies: Dependence structure modeling; adjusted validification under serial correlation.
- Mendelian Randomization ecosystems adopting possibilistic validification (academia; genetics/biostatistics)
- Formalize pleiotropy budgets as A and standardize reporting of partial identification regions across MR studies.
- Tools/products: MR-Possibilistic add-ons, harmonization standards, and visualization utilities for genetic studies.
- Assumptions/dependencies: Cross-consortium agreement on plausible A; integration with existing MR pipelines.
- Decision-support systems under epistemic uncertainty (industry; robotics, supply chain, energy)
- Embed possibilistic posterior concepts (upper/lower probabilities) into operational decision engines that prefer robust actions under partial identification.
- Tools/products: “Epistemic Decision Layer” that consumes possibility functions and returns risk-aware policies.
- Assumptions/dependencies: Mapping from intervals to decision rules; domain-specific cost and risk models.
- Education and training curricula on partial identification and possibility theory (academia; education)
- Courses and professional certifications teaching outer measures, validification, and sensitivity workflows for causal inference.
- Tools/products: Open educational resources; case-based labs (e.g., institutions and growth paper).
- Assumptions/dependencies: Institutional adoption; alignment with existing causal inference syllabi.
- Regulatory audit frameworks for causal claims in AI-driven analytics (policy, industry; AI governance)
- Require reporting of validified possibilistic intervals when causal claims inform consumer impact, pricing, or safety.
- Tools/products: Audit checklists; compliance APIs to verify that α ∈ declared A and intervals are validified.
- Assumptions/dependencies: Regulator buy-in; harmonization with model risk management standards.
- Hybrid probabilistic–possibilistic causal pipelines (academia, industry; machine learning, software)
- Combine Bayesian models with possibilistic priors for components with epistemic uncertainty and partial identification.
- Tools/products: Libraries that allow seamless switch between integration-based and optimization-based uncertainty quantification.
- Assumptions/dependencies: Theoretical guarantees for hybrid models; developer adoption and tooling support.
Collections
Sign up for free to add this paper to one or more collections.