Weight-sparse transformers have interpretable circuits (2511.13653v1)

Abstract: Finding human-understandable circuits in LLMs is a central goal of the field of mechanistic interpretability. We train models to have more understandable circuits by constraining most of their weights to be zeros, so that each neuron only has a few connections. To recover fine-grained circuits underlying each of several hand-crafted tasks, we prune the models to isolate the part responsible for the task. These circuits often contain neurons and residual channels that correspond to natural concepts, with a small number of straightforwardly interpretable connections between them. We study how these models scale and find that making weights sparser trades off capability for interpretability, and scaling model size improves the capability-interpretability frontier. However, scaling sparse models beyond tens of millions of nonzero parameters while preserving interpretability remains a challenge. In addition to training weight-sparse models de novo, we show preliminary results suggesting our method can also be adapted to explain existing dense models. Our work produces circuits that achieve an unprecedented level of human understandability and validates them with considerable rigor.

• The paper presents a novel approach to infuse weight sparsity in transformers, uncovering interpretable circuits via targeted pruning strategies.
• It demonstrates that sparse circuits are up to 16 times more compact and crucial for task performance, as evidenced by rigorous ablation studies.
• The study bridges sparse and dense models, enhancing mechanistic understanding and paving the way for scalable, interpretable neural architectures.

Summary of "Weight-Sparse Transformers Have Interpretable Circuits"

This essay analyzes the paper "Weight-Sparse Transformers Have Interpretable Circuits" (2511.13653), which presents the development and evaluation of weight-sparse transformers aiming for enhanced mechanistic interpretability. The authors explore methods to simplify neural network models by introducing structural sparsity in their parameters, thereby making the circuits within the models more discernible and interpretable. Through careful pruning and analysis, they successfully show that weight-sparse models can yield more transparent representations than dense models, while balancing capability and interpretability.

Introduction to Mechanistic Interpretability

Mechanistic interpretability is focused on understanding the internal workings of neural networks. The challenge with contemporary transformers is the complexity and superposed nature of their activations and weights, which often obscure straightforward human comprehension. Existing methods aiming at overcoming superposition successfully produce partially interpretable representations but often reflect chosen abstractions rather than the model's core computations.

To address these challenges, this paper proposes weight-sparse transformers, which replace dense connectivity with a sparse structure that enforces a small number of active weights per neuron. This approach is posited to reduce distributed representations and encourage concept encapsulation in model nodes, thus, simplifying circuit identification and exploration.

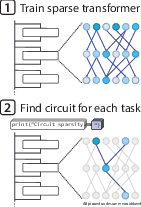
Figure 1: An illustration of our overall setup. Weight-sparse models are trained and pruned to task-specific nodes, simplifying interpretability.

Methods: Sparse Training and Pruning

The authors detail their technique for training and isolating circuits in weight-sparse models. These models are created by setting the $L_0$ norm low, ensuring most weights are zero and each neuron engages with minimal connections. By using a novel pruning strategy, nodes not essential for task performance are systematically removed, revealing compact circuits that maintain task performance post-ablation. This approach yields circuits where neuron activations and residual channels correlate with intuitive conceptual representations.

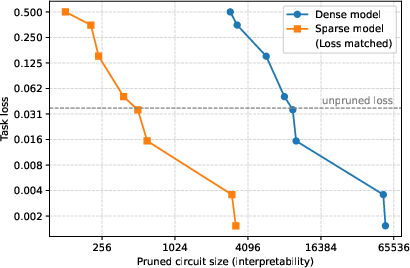
Figure 2: Sparse model circuits are significantly smaller and task-specific compared to dense models, enabling simpler circuit identification at comparable performance losses.

Results: Sparse Models Enable Circuit Simplification

Experiments demonstrate that the sparse models facilitate the discovery and validation of simpler circuits. Comparing dense and sparse models of similar training losses, sparse model circuits are notably more compact, by a factor of 16 on average. Additionally, these sparse circuits are shown to be both necessary and sufficient for task execution, as ablating elements outside these circuits impairs performance further than ablating within the circuit.

Scaling these sparse models improves the capability-interpretability frontier, suggesting that larger sparse models better balance task execution and simplified circuit discovery.

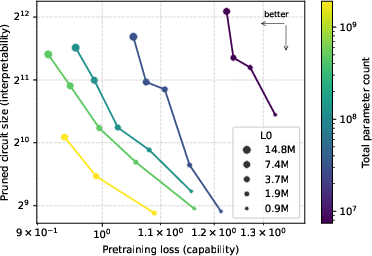
Figure 3: Scaling parameter counts in sparse models improves the capability-interpretability Pareto frontier, demonstrating superior scalability with retained interpretability.

Qualitative Circuit Investigations

Further qualitative examination of task-specific circuits demonstrates mechanistic clarity. In tasks such as closing string detection or counting list nesting depth, sparse circuits are shown to implement intuitive algorithms closely resembling human-understood procedures. These circuits consist of readily interpretable operations within attention layers and MLPs, validated through experimental ablations and observations.

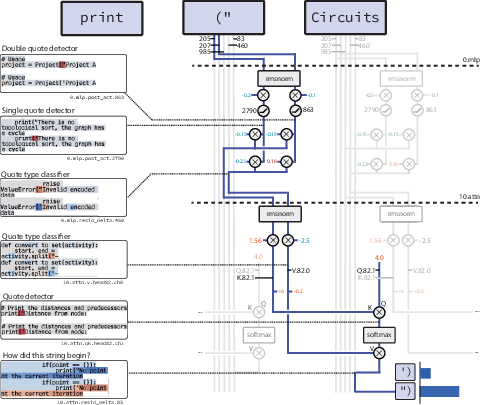
Figure 4: A detailed schematic of a circuit within sparse models for closing string detection, illustrating interpretable node connections and their functional roles.

Bridges: Linking Sparse and Dense Models

Extending sparse training to understand dense models, the paper introduces bridge methods, which couple sparse model activations to dense model counterparts. This integration allows for indirect interpretability methods where sparse models serve as a stand-in to elucidate dense model computations, promising enhanced understanding of existing neural architectures.

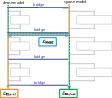
Figure 5: Bridging techniques link sparse and dense models, facilitating interpretable perturbations across model architectures.

Conclusion

The development of weight-sparse transformers marks a substantive step in mechanistic interpretability, providing a structural approach to deciphering neural model computations. By simplifying model architecture and revealing compact circuit structures, the proposed methods advance our understanding and manipulation of LLMs. Future work is anticipated to address the inherent training inefficiencies of sparse models and explore scaling strategies that retain computational clarity, further enhancing interpretability without compromising performance.