PCA++: How Uniformity Induces Robustness to Background Noise in Contrastive Learning (2511.12278v1)

Abstract: High-dimensional data often contain low-dimensional signals obscured by structured background noise, which limits the effectiveness of standard PCA. Motivated by contrastive learning, we address the problem of recovering shared signal subspaces from positive pairs, paired observations sharing the same signal but differing in background. Our baseline, PCA+, uses alignment-only contrastive learning and succeeds when background variation is mild, but fails under strong noise or high-dimensional regimes. To address this, we introduce PCA++, a hard uniformity-constrained contrastive PCA that enforces identity covariance on projected features. PCA++ has a closed-form solution via a generalized eigenproblem, remains stable in high dimensions, and provably regularizes against background interference. We provide exact high-dimensional asymptotics in both fixed-aspect-ratio and growing-spike regimes, showing uniformity's role in robust signal recovery. Empirically, PCA++ outperforms standard PCA and alignment-only PCA+ on simulations, corrupted-MNIST, and single-cell transcriptomics, reliably recovering condition-invariant structure. More broadly, we clarify uniformity's role in contrastive learning, showing that explicit feature dispersion defends against structured noise and enhances robustness.

• The paper introduces PCA++, a contrastive PCA method that enforces a hard uniformity constraint to robustly recover low-dimensional signal subspaces amid structured noise.
• It formulates a generalized eigenvalue problem with covariance truncation to stabilize performance in high-dimensional settings and noisy scenarios.
• Empirical and theoretical results show PCA++ outperforms standard techniques in simulations, corrupted images, and single-cell transcriptomics.

PCA++: Uniformity and Robust Signal Recovery in Contrastive Learning

Introduction and Theoretical Framework

Principal Component Analysis (PCA) is foundational in high-dimensional data analysis but indiscriminately captures dominant variance, rendering it ineffective at isolating low-dimensional signals from strong structured background noise. Inspired by contemporary contrastive learning, the authors introduce PCA++, a constraint-based contrastive PCA method that leverages paired observations—positive pairs sharing a latent signal but differing in independent backgrounds. They formalize this as a contrastive linear factor model, analyze population and finite-sample recoverability, and propose a theoretically-grounded, computationally-efficient solution exploiting a hard uniformity constraint. Theoretical and empirical results demonstrate robust subspace recovery even when both noise and ambient dimension are large, addressing long-standing failures of both vanilla PCA and alignment-only contrastive PCA.

Methodological Contributions

The core methodological result is the introduction of a generalized eigenvalue problem for subspace recovery: maximize the trace of projected contrastive covariance subject to projected features having identity covariance. At the algorithmic level, given $n$ paired samples in $d$ dimensions, with sample covariances $S_n = \frac{1}{n} X^\top X$ and contrastive covariances $S_n^+ = \frac{1}{2n}(X^\top X^+ + X^{+\top} X)$, PCA++ solves

$$\max_{V\in \mathbb{R}^{d\times k}} \operatorname{tr}(V^\top S_n^+ V) \quad \text{s.t.} \quad V^\top S_n V = I_k,$$

optimized by computing top generalized eigenvectors of $(S_n^+, S_n)$. This hard uniformity constraint dynamically regularizes away high-variance background directions, yielding robust estimates even as $d/n$ increases or when background eigenvalues dominate.

An essential practical and theoretical issue is the numerical instability of the eigenproblem when $S_n$ is ill-conditioned for $d \gg n$. The authors introduce covariance truncation: replace $S_n$ by its rank-$s$ principal subspace to stably enforce uniformity and derive conditions for optimal truncation.

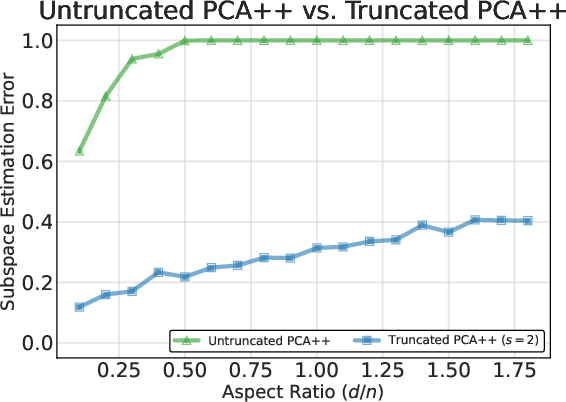
Figure 1: Effect of covariance truncation on the generalized eigenproblem. Proper truncation maintains alignment accuracy as $d/n$ grows, stabilizing PCA++.

Theoretical Results: High-Dimensional Regimes and Signal Recovery

The authors develop an extensive random matrix theory analysis in both fixed aspect ratio and growing-spike regimes:

• Population-level Recovery: Alignment-only contrastive PCA is unbiased and isolates shared signal subspaces when background variation is mild.
• Finite-sample Bounds: The exact non-asymptotic subspace recovery error shows that pure alignment fails when the background spike (i.e., largest eigenvalue) dominates, or $d/n$ is large.
• High-dimensional Asymptotics: In both the fixed aspect ratio ($d/n \rightarrow c > 0$) and growing-spikes (signal and noise eigenvalues scale with $d/n$) regimes, PCA++ achieves small estimation error controlled by the effective signal-to-noise ratio. Crucially, PCA++ is provably stable even as background strength increases, in stark contrast to standard PCA and alignment-only methods.

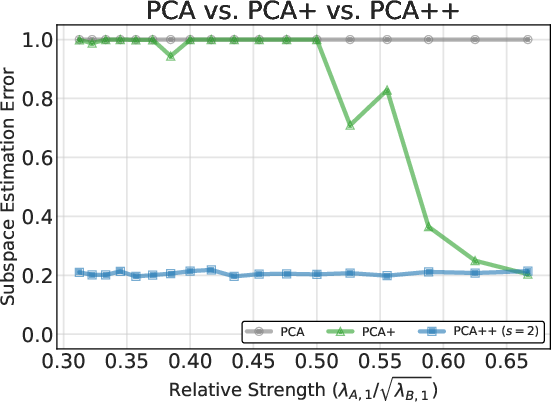
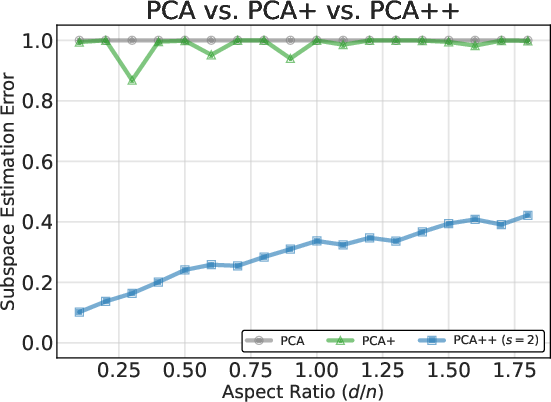
Figure 2: Subspace estimation error for standard PCA, contrastive PCA, and PCA++ across varying background strength and aspect ratio.

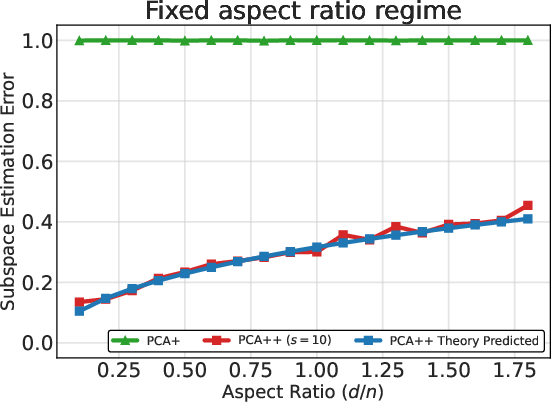
Figure 3: Empirical validation of high-dimensional theoretical predictions for PCA++—alignment with theory in both aspect ratio and growing-spike regimes.

These findings rigorously clarify the statistical role of uniformity: the uniformity constraint acts as a spectral filter, regularizing against background without requiring explicit background-only samples.

Empirical Demonstrations

Synthetic Data

Simulation studies confirm the theoretical predictions. PCA++ not only maintains subspace alignment as both $d$ and noise grow, but also outperforms standard PCA and alignment-only contrastive PCA in both robustness and consistency of error rates.

Corrupted-MNIST Experiment

Using synthetic images comprised of superimposed MNIST digits and ImageNet-derived backgrounds, the authors demonstrate PCA++'s ability to eliminate structured background noise and recover the true digit class separation in low-dimensional embeddings.

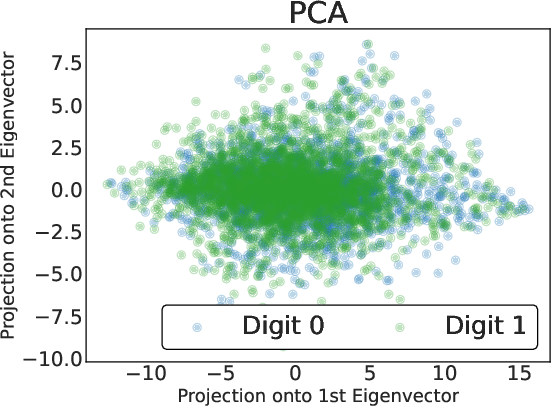
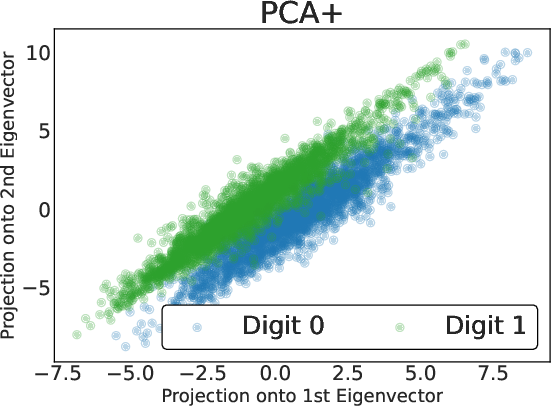
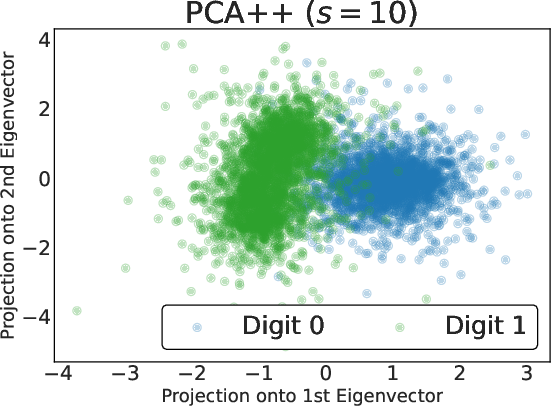
Figure 4: 2D embeddings of noisy digit-over-grass images: standard PCA fails, vanilla contrastive PCA shows partial separation, PCA++ provides clean class distinction along its first eigenvector.

Single-Cell Transcriptomics

On real-world single-cell RNA-seq data, the method accurately recovers condition-invariant manifolds across control and stimulated populations, effectively removing confounding variation and preserving biologically-meaningful dispersion.

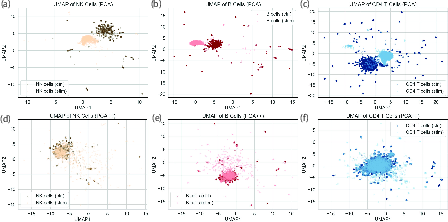
Figure 5: PCA vs. PCA++ embeddings of matched PBMCs—PCA++ better preserves coherent clusters across control and stimulation.

Figure 6: UMAP visualizations show PCA++ aligns control and stimulated conditions, keeping invariant populations coherent and dispersing only truly variable types.

Broader Theoretical and Practical Implications

PCA++ provides a precise, tractable characterization of uniformity’s effect in contrastive learning. The results expose the crucial limitations of pure-alignment approaches and justify explicit uniformity constraints for robustness in high-dimensional applications with structured confounding. The analysis offers a rigorous explanation for the enhancement in performance observed in contrastive learning methods (e.g., SimCLR, Barlow Twins, VICReg) when uniformity is enforced or promoted.

From a practical standpoint, the closed-form, computationally attractive solution represents an advance in dimensionality reduction for domains such as genomics, neuroscience, imaging, and any context where signal is embedded in structured noise. Additionally, the theoretical constructions potentially inform future extensions to nonlinear kernelized settings, sparse subspace recovery, tensor decompositions, and spectral clustering in the presence of nuisance variations.

Conclusion

PCA++ advances the theory and practice of contrastive representation learning by explicitly linking uniformity constraints to robustness against structured background in high dimensions. Theoretical guarantees, robust empirical performance across simulations and scientific data, and computational efficiency collectively position uniformity-constrained contrastive PCA as a principled solution for invariant subspace recovery where standard and alignment-only PCA fail. This work substantiates the role of uniformity as a statistical regularizer and spectral filter, motivating further paper in both linear and nonlinear settings for robust representation learning.

Reference: "PCA++: How Uniformity Induces Robustness to Background Noise in Contrastive Learning" (2511.12278)