A Bayesian Perspective on Evidence for Evolving Dark Energy (2511.10631v1)

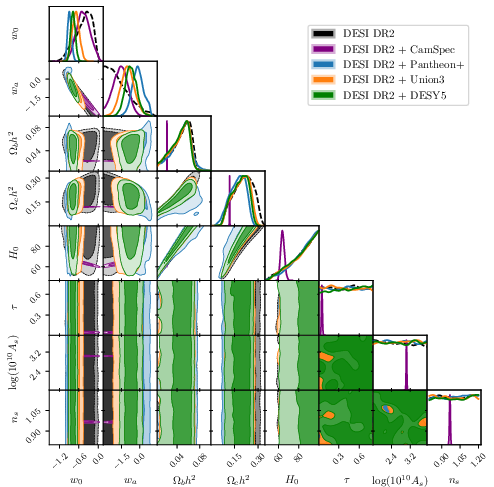
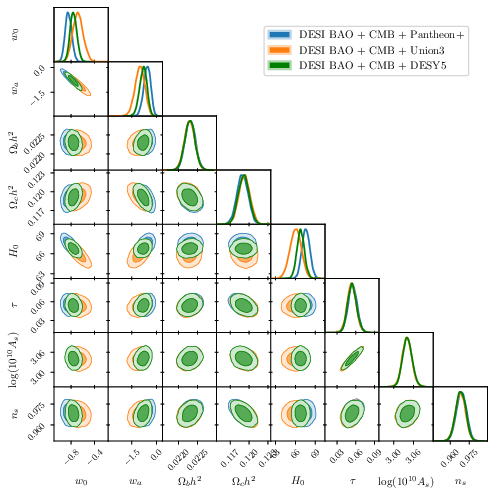
Abstract: The DESI collaboration reports a significant preference for a dynamic dark energy model ($w_0w_a$CDM) over the cosmological constant ($Λ$CDM) when their data are combined with other frontier cosmological probes. We present a direct Bayesian model comparison using nested sampling to compute the Bayesian evidence, revealing a contrasting conclusion: for the key combination of the DESI DR2 BAO and the Planck CMB data, we find the Bayesian evidence modestly favours $Λ$CDM (log-Bayes factor $\ln B = -0.57{\scriptstyle\pm0.26}$), in contrast to the collaboration's 3.1$σ$ frequentist significance in favoring $w_0w_a$CDM. Extending this analysis to also combine with the DES-Y5 supernova catalogue, our Bayesian analysis reaches a significance of $3.07{\scriptstyle\pm0.10}\,σ$ in favour of $w_0w_a$CDM. By performing a comprehensive tension analysis, employing five complementary metrics, we pinpoint the origin: a significant ($\approx 2.95σ$), low-dimensional tension between DESI DR2 and DES-Y5 that is present only within the $Λ$CDM framework. The $w_0w_a$CDM model is preferred precisely because its additional parameters act to resolve this specific dataset conflict. The convergence of our findings with independent geometric analyses suggests that the preference for dynamic dark energy is primarily driven by the resolution of inter-dataset tensions, warranting a cautious interpretation of its statistical significance.

• The paper demonstrates that Bayesian model selection via nested sampling reveals modest evidence for dynamical dark energy primarily when DES-Y5 data is included.
• The authors employ PolyChord with Cobaya and CAMB to compute log-Bayes factors, integrating Occam’s razor to penalize unnecessary model complexity.
• The study highlights that alleviating inter-dataset tensions, especially between DESI BAO and supernova data, drives the preference for the evolving dark energy model.

A Bayesian Re-Assessment of Evidence for Evolving Dark Energy

Introduction

The reported preference for dynamical dark energy models, specifically $w_0w_a$CDM, over the cosmological constant $\Lambda$CDM in recent cosmological data analyses—such as those led by DESI—has motivated intense scrutiny regarding model selection methodologies. This work deploys a direct Bayesian model comparison via nested sampling to critically evaluate the statistical evidence for evolving dark energy. Contrary to frequentist hypothesis tests which often favor $w_0w_a$CDM at high significance when combining baryon acoustic oscillation (BAO), cosmic microwave background (CMB), and Type Ia supernova data, the Bayesian approach reveals a more nuanced landscape where the evidence for new physics is highly sensitive to dataset combinations and the underlying inter-dataset tensions.

Methodology: Bayesian Evidence and Tension Metrics

The analysis leverages the PolyChord nested sampling algorithm for robust Bayesian computation, interfaced via Cobaya and CAMB. The parameter space for $w_0w_a$CDM is bounded following DESI priors, with a physical lower limit on neutrino mass aligned with oscillation data. Bayesian model selection is performed through direct computation of the marginal likelihoods $\mathcal{Z}$ of competing cosmological models; the log-Bayes factor $\ln B$ quantifies the relative support for $w_0w_a$CDM versus $\Lambda$CDM. This method intrinsically implements Occam’s razor, penalizing unnecessary model complexity via prior volume integration.

Significance is conservatively translated from $\ln B$ to frequentist sigma via upper bounds on Bayes factors and established $p$-value relations. Statistical tension between datasets is quantified with the unimpeded evidence framework, encompassing metrics such as evidence ratios, suspiciousness (quantifying direct likelihood conflict), and Bayesian dimensionality (characterizing the parameter subspace where conflicts reside).

Results: Model Preference Is Dataset-Dependent

Bayesian model comparison yields results that diverge substantially from DESI's headline frequentist significances. Individually, DESI DR2 BAO favors $\Lambda$CDM ($\ln B = -1.47 \pm 0.11$). When paired with Planck CMB data—a combination frequently cited as key evidence for evolving dark energy—the Bayesian evidence continues to modestly prefer $\Lambda$CDM with $\ln B = -0.57 \pm 0.26$, contrasting sharply with the 3.1$\sigma$ frequentist preference for $w_0w_a$CDM. Inclusion of Pantheon+ supernova data further strengthens Bayesian support for $\Lambda$CDM.

The preference for $w_0w_a$CDM materializes only when the DES-Y5 supernova catalogue is added. Both pairwise and triplet combinations involving DES-Y5 show positive log-Bayes factors and reach Bayesian significances up to $3.07 \pm 0.10\,\sigma$, though still weaker than the frequentist claims. The origin and dimensionality of model preference are illuminated by dedicated tension metrics, revealing that the $w_0w_a$CDM model is favored due to its ability to mitigate tension between DESI BAO and DES-Y5 data—not because of intrinsic support from BAO or CMB alone.

Figure 1: Posterior constraints in $w_0w_a$CDM parameter space for DESI DR2 alone and in combination with diverse external probes. Visible are significant shifts in $w_0$, $w_a$, and broader cosmological constraints, illustrating how dataset choices impact inferred dark energy dynamics.

Tension Analysis and the Mechanism of Model Selection

The inter-dataset conflict between DESI DR2 BAO and DES-Y5 supernovae is quantified at $2.95 \pm 0.04 \,\sigma$ within $\Lambda$CDM, manifesting as a low-dimensional, local likelihood tension ($d_G \approx 1$), with strongly negative suspiciousness and evidence ratio metrics. This tension is efficiently diffused in $w_0w_a$CDM ($\sigma$ drops to $1.56 \pm 0.03\,\sigma$; $d_G > 3$), highlighting the role of additional dark energy degrees of freedom in accommodating inter-survey inconsistencies.

Triplet combinations (DESI DR2 + CMB + DES-Y5) exhibit even more severe likelihood conflicts within $\Lambda$CDM ($\log S = -5.56 \pm 0.09$), but again, $w_0w_a$CDM expands the parameter space to mitigate these tensions. Other supernova catalogues, such as Pantheon+, demonstrate only mild tension, and do not drive model preference toward dynamical dark energy.

Methodological Discrepancies and Their Roots

The persistent magnitude of discrepancy between Bayesian and frequentist outcomes—especially in combinations involving DESI DR2—cannot be categorically attributed to philosophical differences between paradigms. Instead, questions arise regarding the reliability of asymptotic formulae in frequentist significance calculation, given the finite dimensionality and compression of the DESI BAO dataset. As in particle physics, careful Monte Carlo validation of test statistics’ distributions is standard, and similar nested sampling approaches can bridge frequentist-Bayesian computations. Independent geometric analyses corroborate the Bayesian results, suggesting that published frequentist significances overstate the case for evolving dark energy.

Implications and Future Directions

This paper demonstrates that reported evidence for dynamical dark energy is contingent upon dataset selection, and is primarily an artifact of the $w_0w_a$CDM model’s ability to dilute statistical tension between specific probes. The finding that the DESI BAO and CMB data alone remain consistent with $\Lambda$CDM (with corroboration from geometric approaches) underscores the necessity for cautious interpretation of headline significances in cosmological model selection. Adopted Bayesian workflows offer robustness against overfitting and provide high-dimensional diagnostics for the origins of inter-dataset disagreement.

Further research must focus on the detailed characterization of supernova systematics—particularly in the DES-Y5 catalogue—and rigorous calibration of frequentist statistics for cosmological datasets of modest effective dimensionality. Publicly available nested sampling chains and tension analysis tools (e.g., the unimpeded framework) set a benchmark for reproducibility and transparency in cosmological inference.

Conclusion

A Bayesian nested sampling model comparison yields only modest or non-significant evidence for dynamical dark energy when analyzing DESI BAO and CMB data, contradicting strong frequentist results. Apparent support for $w_0w_a$CDM arises uniquely when incorporating the DES-Y5 supernova dataset, and is diagnosed as the resolution of stark inter-dataset tension rather than a discovery of new physical dynamics. These results highlight the imperative for careful model selection, principled tension diagnostics, and validation of inferential machinery in future cosmological surveys.