Rotational Jamming of Optical Matter Driven by Chiral Light (2511.10170v1)
Abstract: Optical matter (OM), composed of optically bound metallic particles, can be rotated by transferring the spin angular momentum (SAM) of chiral light to the assembly. Rotating OM is a promising platform for optical micromachines, with potential applications in plasmofluidics and soft robotics. Understanding the dynamic states of such Brownian, micro-mechanical systems is a relevant issue. One key problem is understanding kinetic jamming and clogging. Studies of driven multiparticle systems have revealed that under suboptimal driving, the systems can stop moving, showing jamming transitions. It is important to identify dynamic regimes where crowding competes with driving and is susceptible to jamming in the context of optical micromachines. Through experiments supported by numerical simulations, we reveal assemblies with well-defined hexagonal or triangular symmetry that efficiently harness the SAM of incident chiral light, resulting in stable rotation. However, as the plasmonic-particle assembly grows and its dimensions approach the beam waist, new particles can disrupt this order. This causes a transition to a fluid-like state with less-defined symmetry, correlated with a significant reduction in transferred torque, causing rotation to stagnate or cease. We suggest this behaviour is analogous to a rotational jamming transition, where the rotational motion is arrested. Our findings establish a clear relationship between the structural symmetry of the OM assembly and its ability to harness SAM, providing new insights into controlling chiral light-matter interactions and offering a novel platform for studying jamming transitions.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper explores how tiny gold particles can be held together and spun by a laser, forming “optical matter.” The authors show that these particle clusters rotate smoothly when they have neat, regular shapes (like triangles or hexagons). But if the shape gets messy—often by adding just one more particle—the rotation can stall, a bit like a traffic jam. They call this a “rotational jamming transition.”
The big questions the paper asks
- Can groups of light-held particles get “jammed” so their rotation stops?
- What makes rotation work well or fail?
- How do the shape and arrangement (symmetry) of the particle cluster affect how much “twist” (torque) the light can give?
- Can we control this behavior by changing the laser’s focus or the number of particles?
How did they paper it?
Experiments: spinning particles with “twisted” light
- The team used circularly polarized laser light. This kind of light carries spin angular momentum (SAM)—you can think of it as light that has a built-in twist.
- The laser pulls and pushes the particles so they “stick together” without touching. This is called optical binding. Think of it like a spotlight that nudges marbles into a pattern.
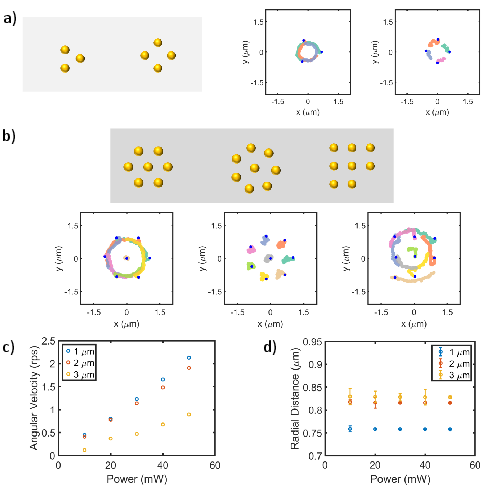
- They used focused beams (small, bright spots) to trap and spin gold nanoparticles (about 400 nm wide—much smaller than a human hair).
- They tested two spot sizes:
- A tighter spot (~1.5 μm wide) that fits fewer particles.
- A slightly wider spot (~2 μm) that fits more particles.
- They watched how groups of particles rotate and tracked their positions over time.
- To measure how “ordered” the shapes were, they used simple symmetry scores:
- A triangular order score (for 3-particle patterns).
- A hexagonal order score (for 6-fold patterns like honeycombs). Higher scores mean more regular shape.
Simulations: checking the physics with computers
- Electrodynamic simulations (using Mie theory) calculated how light pushes on each particle—like predicting how waves bounce off balls. From this, they computed the torque (twist) the light gives to different cluster shapes.
- Dynamic simulations (Langevin dynamics) added “random jiggles” (Brownian motion) to mimic particles in water. These combined the light’s forces, gentle repulsion to prevent overlaps, and natural random motion to see how clusters evolve over time.
What did they find?
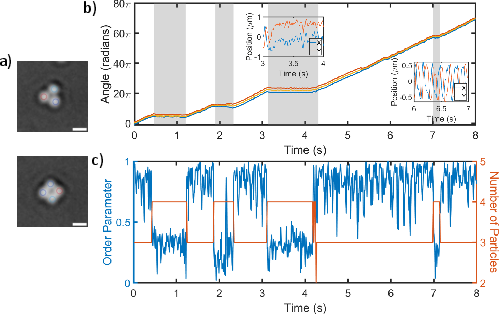
Small clusters: 3 vs 4 particles
- With 3 particles (a triangle), the cluster rotated steadily under circularly polarized light.
- When a 4th particle joined, the shape lost its neat triangular symmetry (often becoming a wobbly square), and rotation stalled.
- If the 4th particle left, the cluster returned to a triangle and rotation started again.
- Translation: symmetry = smooth rotation; broken symmetry = rotation stalls.
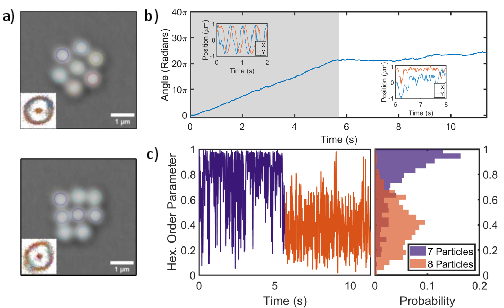
Larger clusters: 7 vs 8 particles (wider laser spot)
- A 7-particle cluster kept a hexagonal pattern and rotated steadily.
- Adding an 8th particle disrupted the hexagonal order; the cluster switched to a “fluid-like” mix of shapes and stopped rotating.
- When that extra particle left, rotation returned.
- Their hexagonal order score dropped sharply at the transition, showing a clear link between shape disorder and loss of rotation.
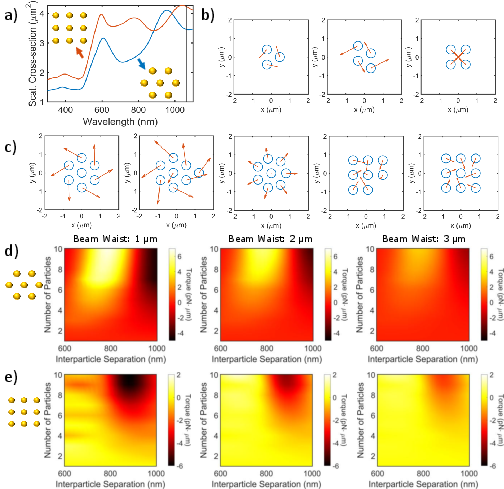
Why symmetry matters (the light–shape link)
- Light’s twist (SAM) is transferred to the cluster as torque when the cluster’s shape is regular. Regular shapes scatter light in predictable “channels,” making torque transfer efficient and positive (it helps the cluster spin).
- Messy or square-like shapes scatter light in changing, inefficient ways. The torque becomes weak, near zero, or even negative (it fights the rotation).
- Simulations agreed:
- Hexagonal/triangular clusters: strong positive torque that grows with more particles (up to a point).
- Square-packed clusters: tiny or negative torque, making rotation slow or impossible.
- Some 8-particle arrangements (like one in the center with seven around) were stable for short times but didn’t orbit the beam in a sustained way.
A new kind of “jamming”
- The team saw a “rotational jamming transition”: rotation stops when the cluster gets crowded and loses symmetry.
- It’s reversible—if the “extra” or “defect” particle leaves, symmetry returns and rotation resumes.
- This is similar to traffic jams: smooth flow with the right number and arrangement, but add one car in the wrong place and everything slows or stops.
Why does this matter?
This research shows a simple design rule for tiny, light-driven machines: keep the cluster’s symmetry clean to get reliable rotation. That has several important impacts:
- Better micromachines: It could help build micro-gears, micro-pumps, and tiny robots powered by light. Engineers can tune the number of particles, their spacing, and the laser’s focus to avoid jamming.
- New ways to control flow: By adding or removing a particle, you can switch rotation on or off—like a microscopic on/off button controlled by light.
- Studying jamming in a new setting: Most jamming studies involve pushing grains or thick liquids. Here, the “driver” is light, not pressure, offering a new playground to understand how order and crowding affect motion.
- Smart design of optical tools: Knowing that square-like or messy shapes kill torque helps plan how to arrange particles and choose laser settings for stable operation.
In short, the paper shows that symmetry is the key to turning light’s twist into reliable rotation. Keep the pattern neat (triangles and hexagons), and the cluster spins. Let the pattern get messy (squares and fluid-like states), and the rotation jams. This insight can guide the creation of future light-powered microscopic devices.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, consolidated list of concrete gaps and open questions that remain unresolved and could guide future research:
- Lack of a quantitative phase diagram: No systematic mapping of rotational states (rotating, stalled, reversed) versus particle number, interparticle spacing, beam waist, NA, power, wavelength, polarization ellipticity/SAM, and material/size; a comprehensive “operating phase space” is missing.
- Critical threshold characterization: The “critical size” at which symmetry loss and rotation arrest occur is shown for two beam waists (3→4, 7→8 particles) but not quantified across conditions; dependence on effective area fraction inside the beam waist, local packing fraction, and cluster geometry remains unmeasured.
- Absence of statistical robustness: Results are illustrated with few exemplars; no ensemble statistics (event frequency, distributions of jamming/unjamming times, reproducibility across trials, sensitivity to initial conditions) are provided.
- Incomplete torque quantification: Torque is inferred from rotation and simulations, but is not experimentally calibrated (e.g., via rotational drag coefficients with wall corrections); direct, quantitative torque measurements and error bounds are lacking.
- Hydrodynamic interactions omitted: EDLD simulations neglect many-body hydrodynamics and wall-induced effects (e.g., Blake tensor, lubrication near the substrate), which are known to strongly affect collective rotation and jamming.
- 2D modeling limitation: Simulations assume strictly planar motion; potential axial (out-of-plane) fluctuations due to strong axial intensity gradients in focused beams are not captured, despite being proposed as a cause of fluid-like states.
- Substrate and near-surface optics ignored: Optical calculations neglect the presence of the glass substrate (index contrast, image fields), which can alter scattering, optical binding, and local field distributions; the assumption that the surface “does not affect optical forces” is not validated for these focused-beam, near-surface, plasmonic conditions.
- Colloidal interaction model mismatch: Using a Lennard-Jones potential for interparticle interactions is not physically faithful for charged citrate-stabilized colloids; DLVO-type interactions (electrostatic + van der Waals) and their dependence on ionic strength are not modeled or measured.
- Thermal/optothermal effects unquantified: Local heating, thermophoresis, and convective/marangoni flows from plasmonic absorption in focused beams are not measured or incorporated; their role in symmetry loss and jamming remains unknown.
- Polarization purity and SAM content at focus not verified: The degree of circular polarization at the focal volume (ellipticity, aberrations, spin–orbit coupling) is not measured; uncertainties in SAM delivery may affect torque and reproducibility.
- Selection-rule verification missing: The discrete rotational symmetry–scattering channel selection rules are invoked via simulations, but no experimental measurement of scattering channel populations or polarization-resolved far-field patterns is provided.
- Negative torque regime unexplored experimentally: Simulations predict small or negative torque for square-packed arrays; experiments report stagnation rather than controlled reversal. Can negative torque states be reliably realized and sustained in practice?
- Controlled unjamming protocols absent: Beyond spontaneous defect escape, strategies to actively unjam (e.g., modulating power, polarization ellipticity/handedness, beam scanning, time-varying SAM, feedback control) are not explored.
- Generality across materials/sizes/wavelengths: While supplementary materials mention other particle sizes and wavelengths, the main text lacks a systematic comparison establishing how jamming thresholds and torque scaling vary with particle size, composition (Au vs Ag), and laser wavelength.
- Beam characterization incomplete: Beam waist values are approximate and back-aperture underfilling is noted but not quantified; full beam profile (intensity and phase, including aberrations) in the sample plane is not measured, limiting predictive modeling.
- Interparticle spacing and binding distance variability: Measured separations (e.g., ~860 nm) are reported, but the distribution, dependence on wavelength/index, and deviations from d_OB=λ/n are not systematically validated across conditions.
- Role of central particles in larger clusters unclear: The effect of placing a particle at the center (e.g., 8P with central inclusion) on torque sign/magnitude and symmetry stability needs systematic assessment.
- Hysteresis and path dependence not tested: Whether transitions between rotating and jammed states exhibit hysteresis, memory, or dependence on assembly history and defect location remains unaddressed.
- Finite-size scaling and criticality: No analysis of critical exponents, scaling laws, or universality class for the rotational jamming transition; it is unknown whether the transition exhibits glassy dynamics or critical slowing down.
- Many-body optical binding effects beyond symmetric lattices: Torque heatmaps are provided for ideal hexagonal/square arrays; the role of irregular, polydisperse, or frustrated packings commonly seen in experiments is not mapped.
- Polydispersity and shape anisotropy: Simulations assume identical spheres; real samples (size/shape distribution, surface roughness) may shift thresholds and torque; their systematic impact is not studied.
- Environmental and chemical controls: Effects of ionic strength, pH, surfactant/citrate concentration, and solvent viscosity on binding, symmetry stability, and jamming are not characterized.
- Substrate properties: Influence of substrate refractive index, roughness, coatings (e.g., PEG), and slip/no-slip boundary conditions on rotation and jamming is not investigated.
- SAM vs OAM beams: Only SAM-driven rotation is studied; whether optical orbital angular momentum (vortex beams) mitigates jamming, alters symmetry requirements, or enables topological control is an open question.
- Multi-cluster interactions: Interactions between multiple assemblies within the same beam or adjacent beams (coupling, synchronization, collective jamming) are unexamined.
- Real-time symmetry sensing and feedback: No implementation of in situ symmetry/order parameter monitoring with feedback to prevent jamming; feasibility of closed-loop control remains unexplored.
- Measurement of rotational drag near surfaces: Accurate models/measurements of rotational friction with wall corrections (Faxén-like) are missing, limiting quantitative torque–speed comparisons.
- Energy landscape reconstruction: The hypothesized “chaotic potential energy landscape” in fluid-like states is not quantified; reconstructing effective energy surfaces from trajectories could validate the mechanism.
- Validation with full-wave electromagnetic models: GMMT/Mie-based methods are efficient but may miss substrate-induced and near-field plasmonic complexities; cross-validation with FDTD/BEM including the wall could resolve discrepancies.
- Temporal spectra of fluctuations: Power spectral density of angle fluctuations, intermittency statistics, and correlation times near the transition are not measured, limiting comparison to active/jammed matter theory.
- Role of handedness and elliptical polarization: Systematic tests of left vs right circular polarization and variable ellipticity to tune torque magnitude/sign and jamming propensity are not performed.
- Long-term stability and drift: Effects of long-term drift, beam pointing stability, and instrument noise on jamming and symmetry stability are not characterized.
Practical Applications
Immediate Applications
The following items translate the paper’s demonstrated phenomena and methods into deployable use cases and workflows that can be implemented now.
- Symmetry-aware control of rotating optical matter in optical tweezers laboratories (academia, research instrumentation)
- Use case: Maintain stable rotation of optically bound nanoparticle assemblies by actively preserving hexagonal/triangular packing and avoiding square or “fluid-like” states that cause torque loss or reversal.
- Tools/products/workflows: Real-time image analysis to compute order parameters (e.g., ψ3, ψ6) from live microscopy (FiJi/TrackMate), feedback control of particle number and arrangement via auxiliary optical traps, selection of circular polarization (SAM), tuning of objective NA and beam waist to keep assemblies below the critical size (beam waist ≈ 1.5–2 μm; stable optical binding distance ≈ λ/n ≈ 1064 nm/1.33 ≈ 800 nm).
- Assumptions/dependencies: 2D confinement near substrate; high-quality circular polarization; stable temperature to mitigate thermally driven defects; particle monodispersity; sufficient imaging SNR; safe handling of IR lasers and metallic nanoparticles.
- Optical “clutch” for microfluidic mixing/pumping (biotech, analytical chemistry)
- Use case: Turn micro-stirrers on/off by adding/removing a “defect” particle to induce rotational jamming; exploit reversible arrest to gate flow or mixing on lab-on-chip platforms.
- Tools/products/workflows: Focused 1064 nm beam with controlled SAM; on-chip chambers hosting 250–400 nm AuNP rotors; automated particle injection/removal to toggle between rotating (ψ6 ≈ 1) and jammed (ψ6 ≈ 0.4) states; calibration via torque–symmetry maps.
- Assumptions/dependencies: Optical access to chip; thermal management (plasmonic heating from AuNPs); fluid compatibility with nanoparticles; reliable particle delivery; precise alignment; rotation rates scale linearly with power (verified via EDLD simulations).
- Microrheology via rotation–torque metrology (materials characterization, biotech QC)
- Use case: Infer local viscosity or viscoelastic changes by monitoring angular velocity and stalling thresholds of hexagonally packed rotors under fixed SAM drive; detect transitions to jammed states as indicators of crowding or matrix changes.
- Tools/products/workflows: Angular trajectory tracking; ψ6 monitoring; calibration curves of torque vs. power and beam waist; standardized reporting of NA, beam waist, ψ6 distributions.
- Assumptions/dependencies: Known particle sizes/materials; minimal out-of-plane forces; reproducible illumination profiles; validated torque models (GMMT/MiePy).
- Rapid diagnostics of nanoparticle monodispersity and surface quality (nanomaterials manufacturing QC)
- Use case: Use sensitivity of rotation to symmetry defects and polydispersity to flag batches with suboptimal size distributions or altered surface chemistry (e.g., aggregation tendencies).
- Tools/products/workflows: Compare measured rotation stability and ψ6 histograms against simulated expectations (MiePy + EDLD); quantify frequency of symmetry-breaking events (4P square states, 8P fluid-like states).
- Assumptions/dependencies: Controlled ionic strength and buffer; stable substrate interactions; consistent laser profiles; correlation between rotation behavior and batch properties.
- Curriculum-ready demonstrations of jamming and SAM-to-OAM transfer (education)
- Use case: Laboratory modules showcasing rotational jamming transitions, symmetry-dependent torque, and active matter concepts using accessible optics.
- Tools/products/workflows: Upright microscope, IR laser (785–1064 nm), AuNP suspensions, FiJi/TrackMate tracking, ψ3/ψ6 order parameter scripts.
- Assumptions/dependencies: Laser safety training; availability of nanoparticles; cost-sensitive adaptations (e.g., lower NA objectives, 785 nm sources).
- Software pipeline for design and control of optical micromachines (software, research instrumentation)
- Use case: Provide an open-source workflow integrating generalized multiparticle Mie theory (MiePy) with overdamped Langevin dynamics for predicting torque maps, stability, and rotation rates; add real-time order parameter computation and closed-loop control.
- Tools/products/workflows: MiePy-based force/torque solvers; EDLD simulation modules; real-time ψ6/ψ3 computation; integration with camera acquisition and trap control.
- Assumptions/dependencies: Computational resources (CPU/GPU); modular API for microscope control; community validation and standard datasets.
- Standardized reporting and reproducibility practices (academia, journals/policy)
- Use case: Adopt common metrics (beam waist, NA, polarization state, ψ3/ψ6 distributions, torque–symmetry heatmaps) to improve cross-lab comparability in optical micromachine studies.
- Tools/products/workflows: Reporting templates; shared calibration protocols; repositories of simulation/experimental benchmarks.
- Assumptions/dependencies: Community buy-in; journal endorsement; availability of reference samples.
Long-Term Applications
These items are enabled by the paper’s principles but require further research, scaling, integration, or validation before broad deployment.
- Reconfigurable optical micromachines (micro-gears, micro-engines, soft robotics)
- Use case: Build light-driven, symmetry-programmable actuators whose function (e.g., pumping, mixing, torque delivery) is toggled by controlled jamming/un-jamming using particle number and arrangement as a “control knob.”
- Tools/products/workflows: On-chip photonic delivery (waveguides/microring couplers), SAM control circuits, microfabricated reservoirs dispensing “defect” particles, embedded symmetry/torque sensors.
- Assumptions/dependencies: Integration with photonics and microfluidics; thermal management; robust operation in complex fluids; long-term stability; materials beyond AuNPs (e.g., biocompatible dielectrics).
- Plasmofluidic networks with torque-gated flow (healthcare diagnostics, analytical chemistry)
- Use case: Arrays of OM rotors orchestrating sample preparation (mixing, lysis, reagent blending) on lab-on-chip devices; flow routing controlled by symmetry-induced “clutches.”
- Tools/products/workflows: Multi-rotor architectures; optical addressing of rotor regions; automated feedback on ψ6; disposable chips with embedded optics.
- Assumptions/dependencies: Manufacturing scalability; optical alignment in disposable formats; regulatory and sterility requirements; minimal photothermal damage.
- Light-driven particle sorters exploiting jamming thresholds (materials, biotech)
- Use case: Design sorting nodes where specific particle types induce symmetry changes that halt or reverse rotation, triggering flow redirect or signaling; leverage torque sign changes (positive in hex arrays; near-zero/negative in square arrangements).
- Tools/products/workflows: Microfluidic geometries that favor symmetry transitions; detection of rotation arrest; control logic for flow switching.
- Assumptions/dependencies: Predictive models linking composition to symmetry states; low false positives; environmental robustness.
- Micromechanical logic using rotational states as bits (software/robotics)
- Use case: Use “rotate” (ordered ψ6 ≈ 1) as 1 and “jam” (ψ6 ≈ 0.4) as 0 for optically addressable logic at the microscale; control swarm microrobots or fluidic sequencing via optical state machines.
- Tools/products/workflows: Spatially multiplexed SAM delivery; state detection and readout; error-correction protocols in fluctuating environments.
- Assumptions/dependencies: Reliable state retention; low energy overhead; scalable addressing and readout; integration with higher-level computation.
- Clinical or in vivo microrobotics (healthcare)
- Use case: Light-actuated microdevices for localized mixing, transport, or sensing inside biological environments.
- Tools/products/workflows: Biocompatible particles (e.g., silica, polymer), longer-wavelength beams with improved tissue penetration, minimally invasive optical delivery systems.
- Assumptions/dependencies: Biocompatibility and clearance; safe power densities; robust actuation in turbid media; regulatory approval; control without substrates (3D stability).
- Environmental and industrial microrheology/sensing (energy, environment monitoring)
- Use case: Portable instruments measuring local viscosity or particulate-induced crowding by monitoring OM rotor behavior; deployable in process control or environmental sampling.
- Tools/products/workflows: Compact optical systems; automated ψ6 and angular velocity analysis; calibration libraries across fluids and temperatures.
- Assumptions/dependencies: Operation in non-ideal, turbid conditions; ruggedization; field calibration; power constraints.
- Nanomanufacturing and directed micro-assembly (advanced materials)
- Use case: Use optical binding and symmetry-controlled torque to orient and assemble building blocks into target lattices; apply symmetry-preserving strategies to avoid jamming during fabrication.
- Tools/products/workflows: Parallelized optical assembly stations; simulation-guided recipes (torque–symmetry heatmaps, stable binding distances); process monitoring via ψ6.
- Assumptions/dependencies: Throughput and yield; compatibility with diverse materials; heating and damage mitigation; cost-effectiveness.
Cross-cutting assumptions and dependencies
- Beam engineering: Precise control of beam waist, NA, and polarization (SAM quality) is critical; focused beams introduce strong gradients and potential out-of-plane forces not fully captured by 2D models.
- Materials and safety: Gold nanoparticle heating and substrate effects must be managed; biocompatibility may require alternative materials and wavelengths.
- Assembly fidelity: Polydispersity and Brownian noise complicate symmetry control; real-time feedback is essential to avoid jamming.
- Modeling vs. reality: Static GMMT/MiePy force maps and 2D EDLD dynamics provide design guidance but must be extended to 3D dynamics, substrate interactions, and complex fluids for robust deployment.
- Scalability: Transition from single-beam, few-particle demos to multi-rotor arrays and integrated photonics will require engineering of alignment, thermal budgets, and manufacturability.
Glossary
- Beam waist: Radius characterizing the narrowest point of a focused Gaussian beam. Example: "as its dimensions approach the beam waist"
- Brownian fluctuations: Random, thermally driven motion of particles in a fluid. Example: "stochastic noise-induced random force representing the Brownian fluctuations."
- Brownian noise: Effective random forcing due to thermal agitation in microscopic systems. Example: "subject to Brownian noise."
- Chiral light: Light with handedness (e.g., circular polarization) that can impart spin-dependent effects. Example: "spin angular momentum (SAM) of chiral light"
- Circular polarization: Light whose electric field rotates uniformly around its propagation axis. Example: "to make the light circularly polarized or chiral."
- Electrodynamic-Langevin dynamic (EDLD) simulations: Coupled optical-force computation with stochastic Langevin dynamics to model particle motion. Example: "Electrodynamic-Langevin Dynamic (EDLD) simulation approach allows us to track the time evolution"
- Focused laser beams: Tightly converged beams that produce strong spatial intensity gradients. Example: "Focused laser beams provide a more efficient method for optical manipulation,"
- Gaussian beams: Laser beams with a Gaussian intensity profile commonly used in optics. Example: "optical matter under circularly polarized Gaussian beams"
- Generalized multiparticle Mie theory (GMMT): Electromagnetic scattering framework for multiple spherical particles. Example: "calculated using GMMT-based simulations."
- Geometric frustration: Inability of a system to satisfy local constraints globally, leading to disordered states. Example: "geometrically frustrated configurations"
- Half-wave plate: Birefringent optical element that rotates linear polarization by a controllable angle. Example: "a polarizer, a half-waveplate, and a quarter-waveplate"
- Hexagonal order parameter (HOP): Metric (ψ6) quantifying sixfold (hexagonal) packing symmetry in an assembly. Example: "The instantaneous local hexagonal order parameter (HOP) of the assembly is plotted"
- Jamming transition: Kinetic arrest where particle motion ceases due to crowding or structural constraints. Example: "analogous to a rotational jamming transition, where the rotational motion is arrested."
- Lennard-Jones interaction: Short-range pair potential modeling attraction and repulsion between particles. Example: "the Lennard-Jones interaction force"
- MiePy: Python package implementing multiparticle Mie theory for optical force and torque calculations. Example: "MiePy"
- Non-equilibrium phase: State of matter maintained away from thermal equilibrium by continuous driving. Example: "Optical matter (OM) is a dynamic, non-equilibrium phase of matter"
- Numerical aperture (NA): Dimensionless measure of an objective’s light-gathering and resolution capability. Example: "a 1.2 NA water immersion objective"
- Optical binding distance: Preferred interparticle spacing set by interference of scattered light in a medium. Example: "the optical binding distance is nearly nm."
- Optical binding force: Light-scattering-induced interaction that self-assembles particles without contact. Example: "The particles are held together by optical binding force, which is a laser scattering-induced interaction."
- Optical matter (OM): Self-assembled particle structures stabilized by optical binding under illumination. Example: "Optical matter (OM), composed of optically bound metallic particles, can be rotated"
- Optical micromachines: Light-driven microscopic mechanical assemblies performing rotational or translational tasks. Example: "Rotating OM is a promising platform for optical micromachines"
- Optical torque: Rotational moment imparted by light due to angular momentum transfer. Example: "result in weak, near-zero, or even negative optical torque."
- Orbital angular momentum (OAM): Angular momentum associated with spatial field structure, distinct from spin. Example: "converted to the OAM of the rotating particle cluster."
- Order parameter (ψ3): Measure quantifying threefold (triangular) symmetry in an assembly. Example: "we defined and calculated an order parameter "
- Plane-wave illumination: Spatially uniform light field with flat wavefronts used in scattering analyses. Example: "plane-wave illuminations that carry spin angular momentum."
- Polarizer: Optical element that transmits a specific polarization state. Example: "a polarizer, a half-waveplate, and a quarter-waveplate"
- Quarter-wave plate: Birefringent optic converting linear to circular polarization (and vice versa). Example: "a polarizer, a half-waveplate, and a quarter-waveplate"
- Right circularly polarised light: Circular polarization with right-handed helicity. Example: "We use a right circularly polarised light, which produces a counterclockwise torque on the particles."
- Scattering cross section: Effective area describing the strength of light scattering by an object or assembly. Example: "The scattering cross-section of optical matter assemblies"
- Scattering modes: Discrete angular-momentum channels into which photons are scattered by a symmetric structure. Example: "the scattering modes of the scattered photons are also well defined and stable."
- Spin angular momentum (SAM): Intrinsic angular momentum of light associated with its polarization. Example: "Beyond linear momentum, light also possesses spin angular momentum (SAM)"
- Spinning optical trap: Optical confinement that imparts rotation via spin angular momentum of light. Example: "focused, chiral, spinning optical trap."
- Viscous drag coefficient: Parameter relating particle velocity to resistive force in a fluid. Example: "where is the viscous drag coefficient"
Collections
Sign up for free to add this paper to one or more collections.