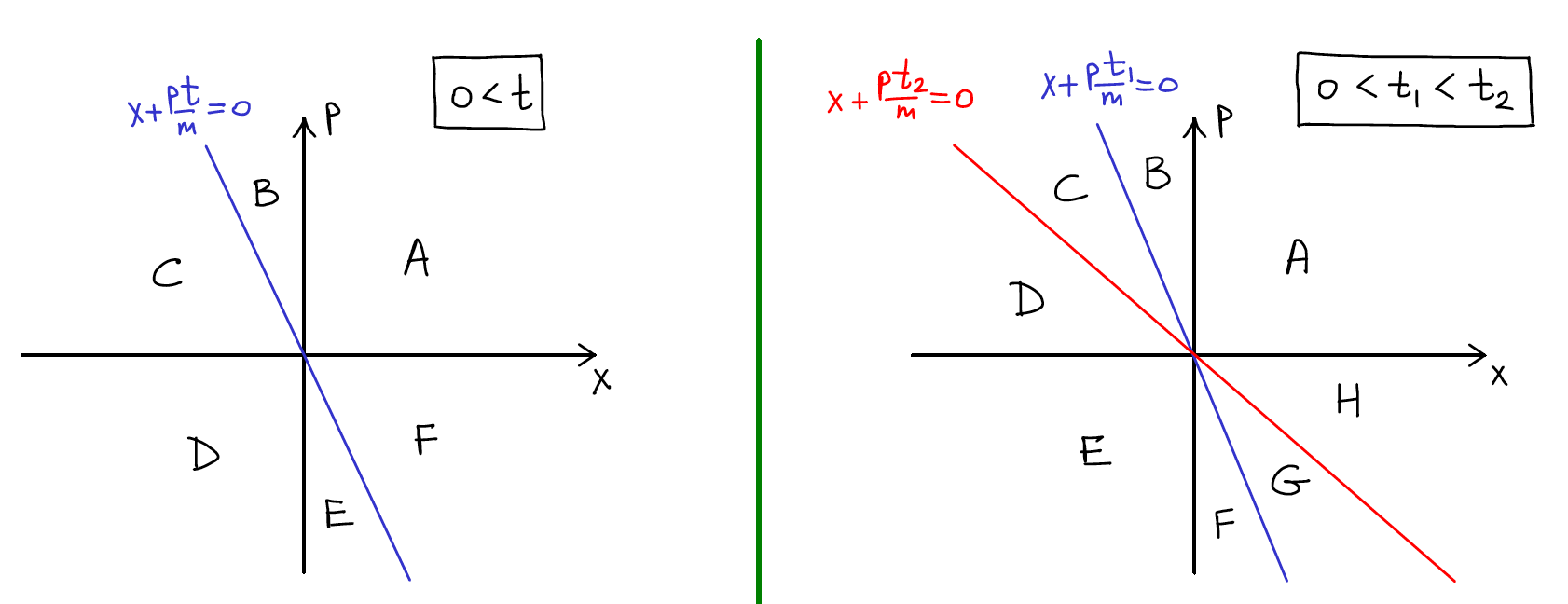General quantum backflow in realistic wave packets (2511.10155v1)

Abstract: Quantum backflow is a counterintuitive phenomenon in which the probability density of a quantum particle propagates opposite to its momentum. Experimental observation of backflow has remained elusive due to two main challenges: (i) the effect is intrinsically small, with less than 4% of the probability able to flow backward, and (ii) it requires wave packets with a well-defined momentum direction, which are difficult both to prepare and to verify under realistic, noisy conditions. Here, we overcome these challenges by introducing a general formulation of quantum backflow applicable to arbitrary momentum distributions. The framework recovers the standard backflow limit for unidirectional states and identifies general backflow as probability flow exceeding that predicted by the particle's momentum distribution alone. We show that this excess can reach nearly 13%, surpassing the standard backflow bound by more than a factor of three. Furthermore, we extend the framework to the closely related phenomenon of quantum reentry, provide explicit examples of quantum states exhibiting large general backflow and reentry, and discuss the foundational implications of these nonclassical effects. Our results open a pathway toward the experimental observation of quantum backflow in realistic settings.

• The paper generalizes quantum backflow to arbitrary momentum distributions, overcoming the need for strictly unidirectional states.
• It employs an integral eigenvalue formulation and numerical analysis to reveal a maximal backflow of approximately 0.1281, significantly exceeding the Bracken–Melloy constant.
• The findings pave the way for experimental tests in cold atoms and mesoscopic systems, opening avenues for robust detection of nonclassical quantum transport.

General Quantum Backflow in Realistic Wave Packets

Overview and Motivation

Quantum backflow represents an anomalous probability flux in quantum mechanics, wherein, for a free particle, probability density may move counter to the classical momentum direction. Despite significant theoretical investigation, experimental observation for matter waves has remained impractical due to two primary limitations: the inherently small magnitude of the conventional backflow effect—bounded by the Bracken–Melloy constant $c_{\mathrm{BM}} \approx 0.03845$—and the necessity of strictly unidirectional (e.g., positive-momentum) wave packets, which are incompatible with realistic quantum state preparation and noisy measurements.

The present work introduces a generalization of quantum backflow to arbitrary momentum distributions, overcoming both limitations. The generalized framework reveals that quantum probability flow exceeding classical bounds is not only more robust under realistic conditions but can also reach values three times larger than the standard backflow bound. These findings have broad implications, both foundational and practical, for the experimental paper of nonclassical effects in quantum transport.

Classical Versus Quantum Bounds for Probability Flow

The classical limit on the evolution of the position probability is derived via phase-space evolution for a free particle. For an arbitrary phase-space density $f(x,p,t)$, the increase in the probability $P_-(t)$ of being left of the origin ($x<0$) is bounded above by the probability of negative momenta $\tilde{P}_- = \int_{-\infty}^0 dp\, f(p)$:

$P_-(t_2) - P_-(t_1) \leq \tilde{P}_-$

Violation of this bound provides a robust, experimentally accessible certificate of nonclassical transport, independent of momentum directionality.

Additionally, the classical reentry bound considers the probability for a particle to reenter a finite spatial interval after having left it. For a region $r=(-s,0)$ and times $t_0 < t_1 < t_2$, the position probability satisfies:

$P_r(t_2) - P_r(t_1) \leq 1 - P_r(t_0)$

Generalizing these inequalities enables the formulation of backflow and reentry observables sensitive to realistic, noisy, and bidirectional states.

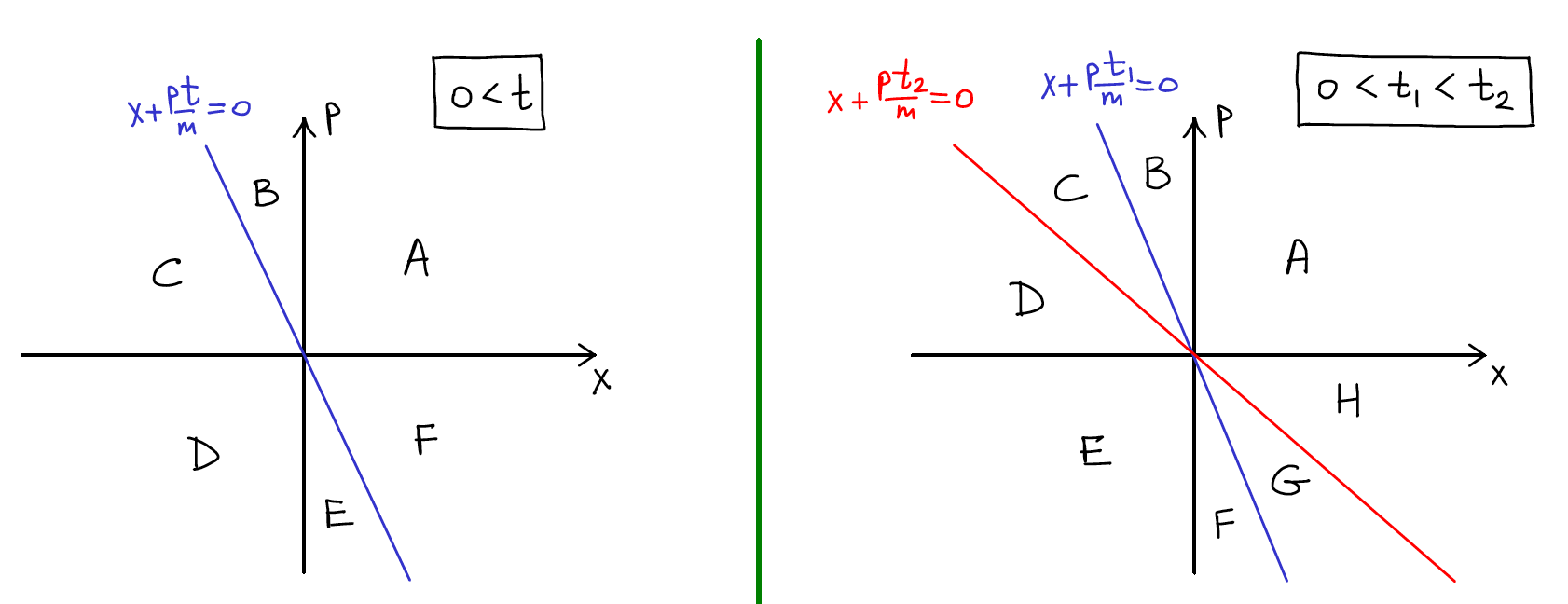
Figure 2: Phase-space diagram illustrating the geometric constraints leading to classical bounds on backflow and reentry; quantum mechanics allows violations of these bounds.

Framework for Generalized Quantum Backflow and Reentry

The quantum backflow observable for arbitrary initial states is given by:

$$\Delta_{\mathrm{QB}} = P_-(t_2) - P_-(t_1) - \tilde{P}_-$$

where $P_-$ and $\tilde{P}_-$ are defined via the position- and momentum-space marginals of the wave function, respectively. The corresponding reentry parameter is:

$$\Delta_{\mathrm{RE}} = P_r(t_2) - P_r(t_1) + P_r(t_0) - 1$$

Both take the form $\Delta = \langle \varphi | K | \varphi \rangle$, where $K(u,u')$ is an explicitly constructed integral kernel, and $\varphi(u)$ is a rescaled initial state. The eigenvector yielding the largest eigenvalue of $K$ supplies the optimizing quantum state for general backflow or reentry.

The central theoretical result is that the supremum $\sup \Delta$ over all normalized states is achieved by solving an integral eigenvalue problem:

$$\int_{-\infty}^{+\infty} du'\, K(u,u')\,\varphi(u') = \lambda\,\varphi(u)$$

Strong Numerical Results and Analytical Bounds

Extensive numerical analysis combining discretization and finite-domain truncation yields the following for the supremum:

$\sup \Delta = 0.128100 \pm 0.000002$

This value is more than three times larger than $c_{\mathrm{BM}}$, marking a decisive increase in accessible quantum backflow. Analytical bounds, derived from recent connections to Tsirelson’s precession inequalities, confirm the numerical result:

$0.128092 \leq \sup \Delta \leq 0.192466$

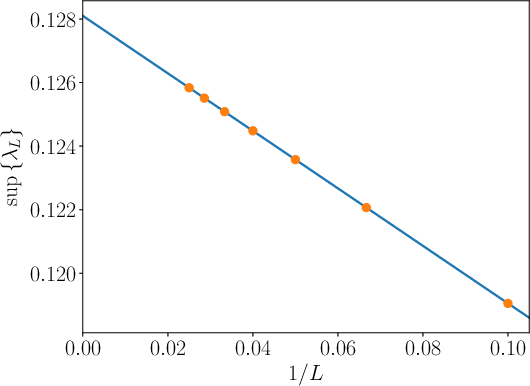
Figure 1: Extrapolation of $\max \{ \lambda_{L,N} \}$ to the $L\to\infty$ limit, confirming convergence of maximal generalized backflow to approximately $0.1281$.

Additionally, explicit construction of physically realizable states shows that even superpositions of two Gaussians—with appropriate parameters—yield $\Delta_{\mathrm{QB}}\approx 0.012$, and more complex asymmetric states can achieve $\Delta_{\mathrm{QB}}\approx 0.062$, both exceeding prior “practical” backflow records.

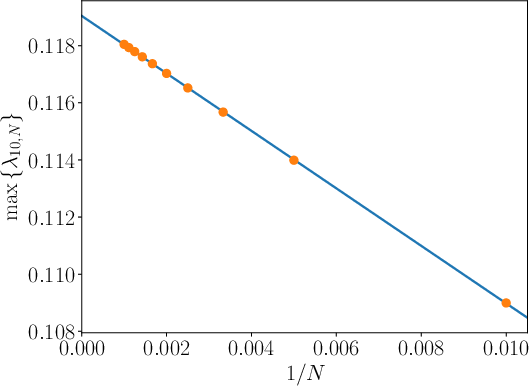
Figure 5: Numerical scaling of $\lambda_{10,N}$ with discretization parameter $N$ for bounded integration domains, consolidating convergence analysis.

Analogous convergence and scaling are reported throughout the eigenvalue calculations (see also Figures 5–10 in the original paper). These demonstrate robustness of the numerical approach and provide a reliable blueprint for computational implementations of backflow optimizations.

Implications for Experiments and Quantum Foundations

The flexibility of the generalized backflow and reentry criteria enables realistic experimental tests based solely on position (and, where feasible, momentum) measurements, without reliance on pure positive-momentum states. This is particularly relevant in settings such as cold atom interferometry, mesoscopic electron transport, and Bose-Einstein condensate dynamics, where state engineering via superpositions or partial momentum filtering is feasible but strict unidirectionality is not.

Crucially, the substantial amplification of quantum violation compared to $c_{\mathrm{BM}}$ suggests that direct detection of probability flow opposite the average momentum is achievable provided suitable post-selection or analysis of marginal distributions. The methodology is inherently robust to experimental noise and state preparation imperfection.

Theoretically, the existence of distinct, universal dimensionless constants (viz., $c_{\mathrm{BM}}$ for standard and $\sup\Delta$ for general backflow) in quantum free evolution prompts deeper inquiries into the landscape of quantum transport phenomena and their connection to quantum pseudo-probability and nonlocality. The explicit trade-off relation between backflow and “forwardflow” further reveals constraints on quantum transport resembling uncertainty-like limitations.

Future Developments

Key open directions include experimental implementation in cold atomic or electron systems using partial position/momentum tomography; optimization of wave packet engineering for maximal observable backflow; extension to interacting or driven systems; and investigation of the relationship between various quantum transport constants and operational quantum information tasks such as certified quantum advantage in state transfer.

Further theoretical work may also elucidate the connection between quantum backflow and phase-space quasi-probability negativity or investigate the effect in systems beyond the non-relativistic, single-particle regime.

Conclusion

This work advances quantum backflow from a mathematically intriguing but practically inaccessible phenomenon to an operationally testable, broadly applicable quantum effect. By generalizing the concept to arbitrary momentum states and deriving both tight theoretical and constructive experimental bounds, the authors establish that quantum probability can flow against classical expectations with an intensity vastly greater than formerly recognized. These results are poised to stimulate both experimental observation and renewed foundational inquiries in quantum transport.