Efficient Reasoning via Reward Model (2511.09158v1)
Abstract: Reinforcement learning with verifiable rewards (RLVR) has been shown to enhance the reasoning capabilities of LLMs, enabling the development of large reasoning models (LRMs). However, LRMs such as DeepSeek-R1 and OpenAI o1 often generate verbose responses containing redundant or irrelevant reasoning step-a phenomenon known as overthinking-which substantially increases computational costs. Prior efforts to mitigate this issue commonly incorporate length penalties into the reward function, but we find they frequently suffer from two critical issues: length collapse and training collapse, resulting in sub-optimal performance. To address them, we propose a pipeline for training a Conciseness Reward Model (CRM) that scores the conciseness of reasoning path. Additionally, we introduce a novel reward formulation named Conciseness Reward Function (CRF) with explicit dependency between the outcome reward and conciseness score, thereby fostering both more effective and more efficient reasoning. From a theoretical standpoint, we demonstrate the superiority of the new reward from the perspective of variance reduction and improved convergence properties. Besides, on the practical side, extensive experiments on five mathematical benchmark datasets demonstrate the method's effectiveness and token efficiency, which achieves an 8.1% accuracy improvement and a 19.9% reduction in response token length on Qwen2.5-7B. Furthermore, the method generalizes well to other LLMs including Llama and Mistral. The implementation code and datasets are publicly available for reproduction: https://anonymous.4open.science/r/CRM.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper looks at how to make AI models think more efficiently. Many advanced LLMs can solve hard math problems by writing out long “chains of thought.” That helps accuracy, but often they “overthink” — they repeat themselves, add unnecessary steps, and waste lots of tokens (which means more time and compute). The authors propose a way to reward models not just for getting the right answer, but also for being concise, so the model learns to think clearly and briefly without losing correctness.
What questions did the researchers ask?
The paper focuses on a few simple, practical questions:
- Can we teach a model to keep its reasoning short while still being correct?
- Why do common “length penalty” tricks sometimes break training or make the model do worse?
- Is there a better reward that balances correctness and conciseness?
- Does this new method improve results across different models and math benchmarks?
How did they do it?
Think of the model as a student. Traditionally, the student gets points only if the final answer is correct (this is called a “verifiable reward” and is common in math tasks). Some research tried to subtract points if the student wrote too much, but that caused two problems:
- Length collapse: the student writes extremely short answers, sometimes skipping real reasoning and “gaming” the system.
- Training collapse: the student’s performance drops badly — both accuracy and output length fall.
To fix this, the authors use two main ideas.
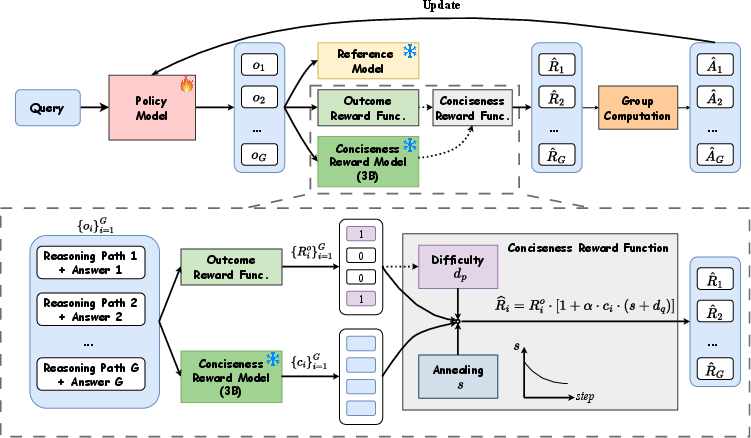
1) Conciseness Reward Model (CRM)
- Imagine a “conciseness judge” that reads a solution and gives it a score for how compact and focused it is.
- How they built it:
- They used a big math dataset (DeepMath-103K) with difficult, diverse problems and existing solutions.
- They asked a strong model to generate two versions of a solution: one that’s concise and one that’s more redundant.
- Another strong model scored these solutions on conciseness (considering repetition, irrelevant steps, and length without hurting quality).
- They trained a smaller model to predict these conciseness scores. This becomes the CRM — a learned judge that can score any reasoning path.
2) Conciseness Reward Function (CRF)
- The key trick: only apply the conciseness bonus if the answer is correct.
- In other words, correctness comes first. If the model is right, then shorter, cleaner reasoning earns extra points. If the model is wrong, it gets no conciseness reward.
- Why this helps:
- It reduces “reward hacking” where the model just prints a short final answer without proper reasoning.
- It gives more stable training by making the reward signal less noisy.
- Two helpful add-ons:
- Annealing coefficient: slowly reduce the weight of conciseness over training. Early on, you encourage conciseness more; later, you let the model settle.
- Difficulty coefficient: harder questions are allowed to have longer reasoning. So the penalty for length is lighter on tough problems and heavier on easy ones.
A note on technical claims (in simple terms)
- Variance reduction: Training is less “noisy,” so updates to the model are more reliable.
- Improved convergence: The model learns faster and more steadily.
What did they find?
The authors tested their method on five math benchmarks (like MATH-500, AIME 2025, OlympiadBench, AMC-23, GPQA) and across several model families (Qwen2.5-7B, Llama 3.1-8B, Mistral 7B).
Key results:
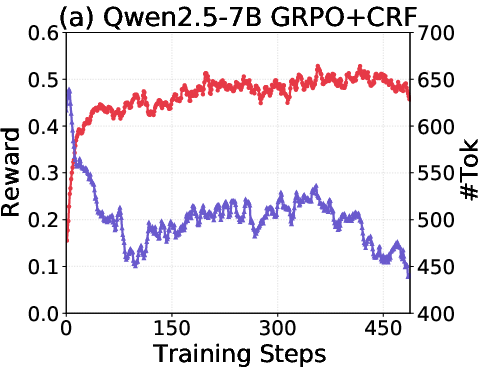
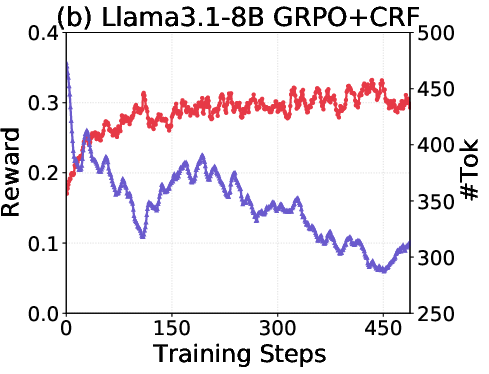
- On Qwen2.5-7B, their method increased accuracy by about 8.1% and cut response length by about 19.9% compared to a strong baseline (GRPO) that rewards only correctness.
- On Llama and Mistral models, it also reduced tokens and often improved accuracy.
- Compared to other “length penalty” methods (like cosine scaling or Kimi 1.5’s length reward), their approach gave a better balance — it reduced length without hurting accuracy as much, and often boosted accuracy.
- Ablation tests (turning off parts of the method) showed the dependency “only reward conciseness when correct” is crucial. Removing it led to worse performance.
A simple example they showed:
- All methods got a math inequality right, but the basic method (GRPO) wrote a lot of unnecessary steps.
- A length-penalized method sometimes just printed the final answer with no reasoning (reward hacking).
- Their method kept reasoning short but still logical, striking a better balance.
Why does this matter?
- Faster and cheaper AI: Shorter answers mean fewer tokens, less compute, lower costs, and quicker responses — especially helpful for large-scale use.
- Better reasoning quality: Encouraging concise, relevant steps trains models to think more clearly, not just more verbosely.
- Safer training: Their reward design avoids common failure modes like length or training collapse, making reinforcement learning more stable.
- Broad usefulness: While they tested on math, the idea of “reward correctness first, then conciseness” could apply to other tasks where clear, efficient reasoning is important (like coding, science answers, or step-by-step explanations).
In short, this paper shows a practical way to train AI to be both smart and efficient: get the right answer, and explain it cleanly.
Knowledge Gaps
Below is a single, concise list of the paper’s unresolved knowledge gaps, limitations, and open questions. Each item is phrased to be concrete and actionable for future work.
- Data/CRM: The Conciseness Reward Model (CRM) is trained solely on math (DeepMath-103K); it is unknown whether CRM scores transfer to other domains (coding, scientific reasoning, step-by-step proofs), other languages, or multimodal settings.
- Data/CRM: CRM labels are produced by LLMs (Qwen2.5-72B) rather than humans; the paper does not quantify label noise, bias, or inter-rater reliability, nor provide calibration of the conciseness scale (0.1–1) against human judgment.
- Data/CRM: The paper does not test robustness of CRM to adversarially concise-yet-misleading reasoning (e.g., omitted critical steps, handwavy jumps), or to stylistic variants (equations-only vs prose, tables, structured proofs).
- Data/CRM: No analysis of CRM error modes (false positives/negatives on conciseness), nor correlation between CRM score and actual length, redundancy, repetition, or reasoning quality across difficulty levels.
- Reward design: The CRF applies conciseness reward only when the outcome is correct; the paper does not explore shaping for partially correct or near-miss reasoning, intermediate verification, or step-level correctness signals to avoid discouraging exploration on hard problems.
- Reward design: The difficulty coefficient d_q uses in-batch group accuracy as a proxy for question difficulty; there is no validation of its reliability, sensitivity to group size G, or comparison to external difficulty estimators.
- Reward design: The annealing schedule s=exp(-step/T) is fixed and heuristic; the paper does not paper its sensitivity, alternative schedules, or adaptive annealing tied to training dynamics (e.g., variance, entropy, or success rate).
- Reward design: CRF provides only positive reward; the impact of adding carefully designed negative rewards for incorrect but overlong or reward-hacking responses is untested.
- Theory: Variance reduction and improved convergence are proved under assumptions (e.g., Cov(R_io, c_i) > 0, unbiased gradient, smoothness); the paper does not empirically verify these assumptions (e.g., measure correlation or gradient variance) or analyze failure when assumptions break (negative/zero covariance).
- Theory: The analysis abstracts away GRPO-specific clipping and sets KL penalty β=0; it remains unclear how CRF behaves with realistic PPO/GRPO settings (nonzero β, clipping effects), and whether theoretical guarantees extend to these regimes.
- Failure modes: While CRF is proposed to mitigate length/training collapse, there is no systematic evaluation of CRF’s own failure modes (e.g., over-pruning legitimate steps on hard problems, hidden reward gaming against CRM, mode collapse under extreme α, s, d_q).
- Generalization: The method is only evaluated on small to mid-size open models (Qwen2.5-7B, Llama3.1-8B, Mistral-7B); scalability to larger LRMs (e.g., 70B+) and to proprietary o1/R1-style systems is untested.
- Generalization: The paper asserts compatibility with other RL algorithms (e.g., DAPO) but provides no empirical results across diverse RLVR/RLHF methods (PPO variants, RLAIF, off-policy methods, step-wise rewards).
- Metrics: Efficiency is proxied by output tokens only; there is no measurement of wall-clock latency, total compute, memory, throughput, or energy, nor analysis of the trade-off with sampling strategies (temperature, Pass@k).
- Metrics: The evaluation relies mainly on Pass@1 and token length; more comprehensive metrics (process correctness, logical soundness, error localization, faithfulness of reasoning, human preference) are missing.
- Baselines: Key efficient reasoning baselines (ALP, LC-R1, other length-penalty methods) are discussed but not consistently benchmarked head-to-head across all datasets and backbones; reproducible comparisons and unified protocols are lacking.
- Hyperparameters: Sensitivity analyses are limited (mostly α); the paper does not explore sensitivity to group size G, max length, CRM backbone size, reward scaling, or the difficulty/annealing functional forms.
- Cold-start: For Llama/Mistral, CRF is used only after SFT due to cold-start issues; it remains open whether CRF can enable zero-shot RLVR training or reduce the amount of required SFT.
- Safety/robustness: No assessment of unintended behaviors under CRF (e.g., hallucinations, unsafe content, shortcutting via spurious correlations, deterioration in non-math capabilities), or whether increased conciseness harms transparency/explainability.
- Reproducibility: Some implementation details (exact prompts, appendices, training seeds, group sizes, reward scaling) are not fully reported in the main text; rigorous reproducibility and formal data release with licensing are required.
- CRM at inference: The paper does not investigate leveraging CRM at inference time (reranking, early-exit, stop-when-confident), nor compare training-time vs inference-time gains for efficiency.
- Process-level rewards: The approach scores whole-answer conciseness; it leaves unexplored step-level conciseness rewards, local redundancy detection, or structured reasoning-format constraints that could provide finer-grained guidance.
- Domain shift: The difficulty-aware length adjustment is motivated by DeepMath statistics; its effectiveness under domain shift (different benchmarks, task distributions, or non-verifiable tasks) is unknown.
Practical Applications
Overview
This paper introduces a training pipeline and reward design that make large reasoning models (LRMs) both more accurate and more concise. It trains a Conciseness Reward Model (CRM) to score reasoning paths and proposes a Conciseness Reward Function (CRF) that applies conciseness rewards only when answers are correct. Empirically, the method reduces token usage while improving accuracy; theoretically, it reduces gradient variance and improves convergence. Below are practical applications organized by timeframe, including sector links, potential tools/workflows, and feasibility considerations.
Immediate Applications
The following applications can be deployed now with modest engineering effort, using available RLVR tooling (e.g., GRPO/DAPO), existing LLM backbones (Qwen, Llama, Mistral), and the CRM/CRF designs described in the paper.
- Industry (AI/Software Engineering)
- Use CRF in RLVR post-training for math, coding, and tasks with verifiable outcomes (e.g., unit-testable code generation), to improve accuracy while cutting response tokens and latency.
- Sector: software
- Tools/workflows: integrate CRM as a module in existing RL pipelines (GRPO/DAPO); adopt difficulty-aware and annealed conciseness weighting; track Pass@k and tokens in training dashboards; deploy shorter CoT models for production.
- Dependencies/assumptions: availability of verifiable rewards (tests/validators); CRM is trained on domain-appropriate data; assume positive correlation between correctness and conciseness; compute resources for RL.
- Cost and throughput savings for model-serving platforms by deploying concise reasoning variants for math/coding assistance and structured tasks.
- Sector: software, energy
- Tools/products: “token-budget governor” in inference; model routing to concise variants; capacity planning based on token reductions (~20–40%).
- Dependencies/assumptions: stable performance across workloads; alignment with product UX (concise vs. explanatory); monitoring for failure modes (length collapse/training collapse).
- Faster, more stable RL training jobs due to variance reduction and improved convergence constants.
- Sector: software (ML platform)
- Tools/workflows: reduced wall-clock and GPU-hours; tighter learning-rate schedules enabled by lower gradient variance.
- Dependencies/assumptions: CRF’s variance reduction holds in the target domain; proper group sampling (G) and batch design; reward signal quality.
- Concise developer assistants and code review bots that reward brevity only on correct outputs (tests pass).
- Sector: software
- Tools/products: CI-integrated assistants; concise rationales; guardrails that incentivize short explanations when test suites succeed.
- Dependencies/assumptions: robust unit/integration tests; domain-specific CRM fine-tuned on code reasoning; careful tuning of α (conciseness weight).
- Customer support bots that solve ticket workflows (with verifiable resolution states) and provide minimal but sufficient steps.
- Sector: software (customer support), finance (operations), education (helpdesk)
- Tools/workflows: resolution-state checkers as verifiers; CRM-guided training for concise troubleshooting scripts.
- Dependencies/assumptions: clear verifiable endpoints (issue resolved/knowledge article matched); CRM tuned to support narratives without losing crucial steps.
- Academia
- A reproducible method to paper and mitigate “overthinking” in reasoning models, replacing crude length penalties with a learned conciseness model and correctness-dependent rewards.
- Sector: education, research
- Tools/workflows: open datasets (DeepMath), CRM training with synthetic labels, ablation frameworks to test collapse phenomena; benchmarking token efficiency alongside accuracy.
- Dependencies/assumptions: access to sufficiently strong teacher models for synthetic labeling; domain decontamination; reproducibility standards.
- A template for building new reward models for other preferences (clarity, safety, faithfulness), plugging into CRF-like correctness-dependent reward chaining.
- Sector: research
- Tools/products: “AutoRM builder” pipeline; plug-in reward functions for RLVR frameworks.
- Dependencies/assumptions: availability of preference data or high-quality synthetic labeling; reliable verifiers for the base outcome reward.
- Policy and Governance (near-term operations)
- Compute/energy efficiency reporting for reasoning systems using token-length and accuracy metrics; operational policies that favor CRF-trained models for verifiable tasks.
- Sector: policy, energy
- Tools/workflows: dashboards tracking accuracy vs. tokens; procurement checklists requiring concise inference where verifiable rewards exist.
- Dependencies/assumptions: well-defined KPIs; cross-team buy-in; no degradation in safety or coverage due to shorter reasoning.
- Daily Life
- Concise math tutors and homework helpers that still show necessary steps, tuned by difficulty-aware length penalties.
- Sector: education
- Tools/products: paper assistants with adjustable verbosity; settings for step granularity by problem difficulty.
- Dependencies/assumptions: CRM generalizes to the curriculum; difficulty estimation works in non-exam contexts; UX controls for verbosity.
Long-Term Applications
These require further research, scaling, domain adaptation, or regulatory frameworks before broad deployment.
- Cross-Domain Conciseness Reward Models (beyond math)
- Train CRMs for medicine, law, finance, and scientific writing, scoring redundancy and relevance in discipline-specific reasoning.
- Sectors: healthcare, legal, finance, education, research
- Tools/products: domain-specific CRMs; correctness-dependent CRF calibrated to verifiers (e.g., clinical decision support rules, legal citation checkers, backtesting validators).
- Dependencies/assumptions: strong, reliable verifiable reward signals per domain; expert-labeled or high-quality synthetic preference data; rigorous safety validation.
- Multimodal planning conciseness (e.g., robotics task plans), rewarding short, correct action sequences.
- Sector: robotics
- Tools/workflows: plan verifiers (task completion detectors); CRM for plan succinctness; CRF applied only when tasks are successfully executed in sim/hardware.
- Dependencies/assumptions: robust task verifiers; accurate simulators; transfer from simulation to real-world; safety constraints.
- Regulated and Safety-Critical Systems
- Clinical and legal decision support that maintains necessary justification while minimizing extraneous steps; configurable verbosity to meet documentation standards.
- Sectors: healthcare, legal
- Tools/products: dual-mode outputs (concise for operations, full justification for audit); CRF tuned to reward sufficiency thresholds, not just minimality.
- Dependencies/assumptions: audited verifiers; compliance requirements satisfied; human-in-the-loop oversight; risk management for omission errors.
- Finance and Trading Analytics
- Strategy generation and risk analysis with verifiable backtest rewards; encourage shorter, more direct analysis narratives once correctness (profitability) is established.
- Sector: finance
- Tools/workflows: backtesting verifiers; CRM tuned to financial reasoning; token-efficient reporting pipelines.
- Dependencies/assumptions: robust, non-leaky backtest frameworks; prevention of reward hacking; regulatory compliance for model use.
- Policy and Standards
- Efficiency-first AI governance: standards that require reporting token efficiency and accuracy under verifiable tasks; incentives for CRF-like reward chaining that reduces reward hacking.
- Sector: policy, energy
- Tools/workflows: benchmarking protocols (Pass@k, tokens, collapse detection); carbon-aware compute accounting; procurement language endorsing correctness-dependent rewards.
- Dependencies/assumptions: consensus on metrics; independent audits; sector-specific verifiers (e.g., coding tests, math solvers).
- Tooling and Infrastructure
- RLVR toolkits with plug-and-play CRF, difficulty estimation, and annealing schedulers; monitoring for length/training collapse and variance.
- Sector: software (ML platforms)
- Tools/products: CRF plugins for major RL frameworks; “Collapse Detector” monitors; training orchestration for multi-domain CRMs.
- Dependencies/assumptions: widespread framework support; evolving best practices for hyperparameter tuning; standardized logs.
- Education at Scale
- Curriculum-aware conciseness controllers: adaptive verbosity based on student proficiency and problem difficulty, with verifiable answer checks (auto-graders).
- Sector: education
- Tools/workflows: difficulty estimators; auto-graders as verifiers; personalized verbosity profiles across topics.
- Dependencies/assumptions: reliable proficiency models; coverage of verifiable tasks; fairness and accessibility concerns addressed.
Key Assumptions and Dependencies Across Applications
- Verifiable reward signals exist and are accurate for the target task (e.g., unit tests for code, auto-graders for math, validated rules for clinical/legal contexts).
- Conciseness correlates positively with correctness in the target domain (Cov(R, c) > 0); if not, CRM must be retrained or retuned.
- CRM generalization beyond math requires domain-specific datasets, labeling protocols, and potentially human expert oversight.
- Synthetic labeling relies on strong teacher models; quality control and decontamination are necessary to prevent bias and leakage.
- Proper hyperparameter tuning (e.g., α, annealing schedules, difficulty coefficients) and monitoring for reward hacking and collapse phenomena are essential.
- Shorter reasoning may trade off transparency; products must provide configurable verbosity and audit modes to satisfy safety/compliance.
- Compute availability for RL post-training and data constraints (licensing, privacy) may limit immediate adoption in some settings.
Glossary
- Ada-GRPO: An adaptive variant of GRPO used to train reasoning models. "ARM~\citep{wu2025arm} proposes trained with Ada-GRPO with format diversity reward to support adaptive reasoning formats."
- Advantage: A scalar that measures how much better an action is compared to a baseline, used to weight policy gradients. "where is a clipping-related hyper-parameter to stabilize training and denotes the advantage."
- ALP: A method that applies adaptive length penalties during RL to control reasoning length. "using ALP~\citep{xiang2025just} in Fig.~\ref{fig:analysis}(b)"
- Annealing coefficient: A time-decaying scalar used to gradually reduce the weight of a term during training. "an annealing coefficient is introduced that decays with increasing training steps where and denote the current training step and the total number of training steps, respectively."
- Binary verifiable reward: A reward that returns 1 for a correct answer and 0 otherwise under verifiable checking. "The reward function is usually set as binary verifiable reward considering the correctness of answer:"
- Cardinality: The number of elements in a set. "where denotes the cardinality of a set and this coefficient ranges from 1 to e."
- Clipping (policy optimization): A technique that limits the change in policy ratios to stabilize training. "where is a clipping-related hyper-parameter to stabilize training"
- Conciseness Reward Function (CRF): A reward function that applies conciseness scores only when answers are correct. "we introduce a novel reward formulation named Conciseness Reward Function (CRF) with explicit dependency between the outcome reward and conciseness score,"
- Conciseness Reward Model (CRM): A reward model trained to score how concise a reasoning path is. "we propose a pipeline for training a Conciseness Reward Model (CRM) that scores the conciseness of reasoning path."
- Convergence rate: The speed at which an optimization method approaches a stationary point. "achieves a convergence rate of with improved constants:"
- Cosine scale reward: A length-shaping reward based on a cosine schedule to control CoT length. "Cos~\citep{yeo2025demystifying} denotes the cosine scale reward, which is proposed to stabilize the length scaling of RL training and control CoT length."
- DAPO: A state-of-the-art RL algorithm for LLM post-training; the proposed method is compatible with it. "it can also be easily applied in different state-of-the-art RL algorithms like DAPO~\citep{yu2025dapo}."
- Decontamination procedure: Dataset cleaning to remove training–evaluation overlap. "It undergoes decontamination procedure."
- Difficulty coefficient: A factor that scales reward by estimated problem difficulty. "calculate a difficulty coefficient for each question accordingly:"
- Group Relative Policy Optimization (GRPO): An RL algorithm that optimizes group-sampled responses with relative advantages. "In this section, we provide the background of Group Relative Policy Optimization (GRPO)~\citep{shao2024deepseekmath}, which is a representative reinforcement learning algorithm in reinforcement learning with verifiable rewards (RLVR)."
- KL-divergence penalty: A regularizer penalizing deviation from a reference policy using KL divergence. "The coefficient of the KL-divergence penalty is set to 0 in this paper for simplicity in optimization,"
- Kimi 1.5 reward: A reward that adds a length term to the outcome reward to improve token efficiency. "Kimi~\citep{team2025kimi} represents the Kimi 1.5 reward which adds a length reward to the original outcome reward to improve token efficiency."
- Large reasoning models (LRMs): LLMs optimized (often with RL) for multi-step reasoning. "enabling the development of large reasoning models (LRMs)."
- LC-R1: A length-compression approach for large reasoning models. "cosine scale reward~\citep{yeo2025demystifying}, ALP~\citep{xiang2025just}, and LC-R1~\citep{cheng2025optimizing}."
- Length collapse: A failure mode where response length collapses while reward appears to improve. "We refer to this phenomenon as `length collapse',"
- Over-thinking: Producing excessively verbose, redundant reasoning steps. "This `over-thinking'~\citep{chen2024not} issue introduces significantly heavy computational overhead."
- Pass@: An evaluation metric that checks if at least one of k samples is correct. "the Pass@ metric is adopted,"
- Policy model: The probabilistic mapping from prompts to token sequences parameterized by θ. "the LLM with parameters is denoted as a policy model ."
- Reinforcement learning from human feedback (RLHF): Training that uses human preference data to learn a reward model or policy. "the most common way is to train a reward model from the data annotated by human in reinforcement learning from human feedback (RLHF)."
- Reinforcement learning with verifiable rewards (RLVR): RL that uses rule-verifiable signals (e.g., answer correctness) as rewards. "Reinforcement learning with verifiable rewards (RLVR) has been shown to enhance the reasoning capabilities of LLMs,"
- Reward hacking: Exploiting the reward function to get high reward without truly solving the task. "We refer to this phenomenon as `length collapse', which indicates reward hacking~\citep{skalse2022defining}."
- R1-like training: A two-stage regimen: SFT followed by RL (as popularized by R1-style systems). "Therefore, for these two backbones the R1-like training is adopted,"
- Stationary point: A parameter setting where the gradient is zero. "where is the total number of training steps, is a stationary point."
- Stochastic gradient estimator: A random, unbiased estimate of the true gradient used in SGD-style updates. "exhibits reduced variance of stochastic gradient estimator "
- Supervised fine-tuning (SFT): Supervised fine-tuning of LLMs on input–output pairs. "The training set is leveraged to train the conciseness reward model through supervised fine-tuning (SFT)"
- Variance reduction: Techniques or properties that lower gradient estimator variance, improving stability. "Proposition 1. Variance Reduction: Under the assumption that conciseness reward is positively correlated with outcome reward "
- Zero-R1: Direct RL training of a base model without prior SFT. "directly conduct RL training (same as Zero-R1~\citep{liu2025understanding})."
Collections
Sign up for free to add this paper to one or more collections.