Information Processing in Quantum Thermodynamic Systems: an Autonomous Hamiltonian Approach (2511.08858v1)

Abstract: Extending the quantum formulation of [Phys. Rev. X 3, 041003 (2013)] to a more general setting for studying the thermodynamics of information processing including initial correlations, we generalize the second law of thermodynamics to account for information processing in such autonomous systems. We consider a composite quantum system consisting of a principal system, heat bath, memory, and work source, and adopt an autonomous Hamiltonian framework. We derive constraints on the total Hamiltonian that ensure the work source to act as a catalyst preserving its original randomness, namely that the total unitary evolution must have a unitary partial transpose. We show that this requirement is equivalent to the commutativity of operators acting on the joint system of the principal system, bath, and memory, which underlies the Hamiltonian structure. Next, we generalize the quantum speed limit for the joint dynamics of system and memory to the quantum thermodynamic speed limit, from which we obtain a dynamical version of Landauer's bound. More importantly, we also interpret this quantum thermodynamic speed limit in the context of quantum hypothesis testing.

• The paper introduces an autonomous quantum Hamiltonian framework that rigorously formulates quantum thermodynamic laws.
• It derives strict constraints ensuring the work source acts catalytically by preserving von Neumann entropy during system evolution.
• It establishes a quantum thermodynamic speed limit and links it to quantum hypothesis testing for state discrimination.

Information Processing in Quantum Thermodynamic Systems: Autonomous Hamiltonian Approach

This paper advances the theoretical foundation for quantum thermodynamic information processing by generalizing the classical autonomous Hamiltonian framework to the quantum domain. The authors rigorously construct a closed "quantum universe" comprised of a principal system, heat bath, memory, and work source, governed by time-independent Hamiltonians, and formulate self-consistent thermodynamic laws for quantum information processing—explicitly incorporating initial system-bath-memory correlations and catalytically preserved randomness in the work source.

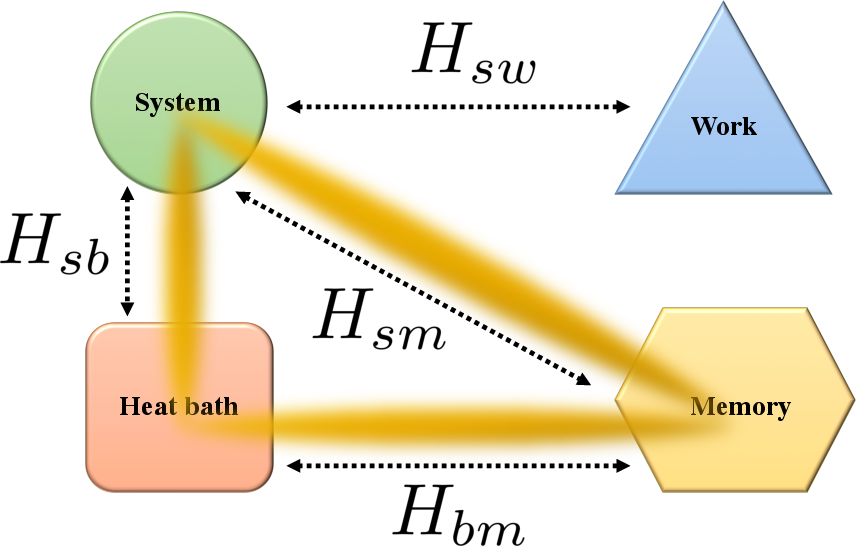
Figure 1: The autonomous quantum universe comprises initially correlated system, bath, and memory, while the work source is uncorrelated and acts catalytically as a source of randomness without entropy loss.

Autonomous Quantum Hamiltonian Framework

By building on the classical theory of autonomous Hamiltonians for information reservoirs, the paper rigorously formalizes the quantum setting: all components (system, bath, memory, work source) are treated as subsystems within a time-independent, closed, and global Hamiltonian framework. The authors derive necessary algebraic constraints for thermodynamic consistency:

• The work source preserves its von Neumann entropy for arbitrary states, enforced by requiring unitary partial transposes of the global evolution operator with respect to the work source's Hilbert space.
• This is equivalent to demanding commutativity among subsystem operators in the system-bath-memory sector, and that all work-source operators commute with the work state, i.e., $[B_j, \rho_w]=0~\forall j$.

This yields a restrictive but physically well-motivated class of total Hamiltonians that guarantee the work source acts as an ideal catalyst. Notably, these constraints avoid the necessity for classical large inertia limits, since quantum resource theory constructions ensure unital maps from such bipartite unitaries.

Formulation of Quantum Thermodynamic Laws

With the Hamiltonian structure in place, the paper articulates quantum analogues of the laws of thermodynamics:

• First Law: The change in internal energy of the principal system equals the sum of heat dissipated from the bath and work supplied by the work source. The memory, modeled as a fully degenerate energy reservoir ($H_m\propto\mathbb{I}$), does not contribute energetically.
• Second Law: The generalized entropy balance incorporates von Neumann entropic changes in the system and memory, and quantum relative entropy (mutual information) arising from initial correlations. This leads to a quantum Landauer bound:

$$\Delta S(\rho_s)+\Delta S(\rho_m) \geq \beta Q_\text{eff}$$

A critical technical point: the energetic cost of information erasure and redistribution depends not only on subsystem dynamics but on tripartite initial quantum correlations, which enter via the quantum relative entropy term.

Quantum Thermodynamic Speed Limit (QTSL)

The authors define the Quantum Thermodynamic Speed Limit (QTSL) for the joint system-memory evolution using Schatten $p$-norms—a mathematically robust measure that generalizes conventional trace and Hilbert–Schmidt distances:

• QTSL time $T^{\star}_p$ is established as a meaningful upper bound on the rate of thermodynamic resource exchange, including entropic information transfer between system and memory.
• The QTSL and its explicit analytic form are derived for several example states, including C-maybe and Werner-like states (see Appendices). Importantly, for Werner-like states, strong numerical evidence establishes that the QTSL is independent of the entanglement parameter ($\lambda$)—an observation that conflicts with intuition regarding entanglement's centrality in quantum speed limits.

  Figure 2: Dependence of the QTSL of order~1 on $\theta$ and $\tau$ for the C-maybe state, quantifying the nontrivial interplay of interaction time and quantum state geometry for information processing efficiency.

  

  Figure 3: QTSL landscape for Werner-like states in the $Z_s \otimes X_m$ basis, revealing marked dependence on superposition parameter $\varphi$ and revealing regions of high speed limit sensitivity.

  

  Figure 4: QTSL for Werner-like states in the $X_s \otimes X_m$ basis, showing independence on $\varphi$ and characteristic periodic behavior as function of the interaction time.

The analyses reveal that while the Hamiltonian’s structure, initial state geometry, and subsystem basis choices have significant impact, entanglement alone does not universally enhance or constrain quantum thermodynamic speed limits. This counterintuitive result underscores the necessity of detailed context-dependent analysis for physical quantum processors.

Operational Link: Quantum Hypothesis Testing

The paper establishes a concrete operational interpretation for QTSL in the context of quantum hypothesis testing:

• Via quantum Stein’s lemma, the asymptotic scaling of type-II error probabilities ($p_n(\tau)$) in distinguishing the evolved state from its equilibrium counterpart is bounded above by an expression containing the QTSL.
• The QTSL thus quantifies the maximal allowable rate for statistically significant state discrimination, directly connecting thermodynamic resource exchange to algorithmic distinguishability.

Implications and Future Directions

The framework unifies energetic and temporal constraints for quantum information processing, with practical relevance for thermodynamically optimal quantum device engineering and quantum algorithm design. The explicit connection between Landauer bounds and quantum speed limits promises robust estimates for resources required in scalable, fault-tolerant quantum architectures—especially as quantum machines transition into regimes dominated by nontrivial initial correlations and non-negligible memory effects.

Highlighted results, such as the independence of QTSL from entanglement parameters in certain families of initial states, suggest that device optimization should be guided by subsystem interaction geometry and Hamiltonian symmetries rather than solely entanglement measures.

In future work, extending these Hamiltonian and speed limit constraints to time-dependent (driven) scenarios, non-Markovian environments, and non-stationary memory reservoirs is likely to yield refined protocols for energy-efficient, temporally optimized quantum information manipulation.

Conclusion

This paper constructs a rigorous autonomous Hamiltonian theory for quantum thermodynamic information processing, generalizing classical thermodynamic laws and speed limits to encompass initial subsystem correlations and quantum memory effects. The derived Hamiltonian constraints, generalized second law, and quantum thermodynamic speed limit together define sharp bounds for energetic and temporal resource requirements in quantum information processing. The operational link to hypothesis testing paves the way for principled resource certification in practical quantum devices. The results challenge the utility of entanglement-centered metrics for speed limits, highlighting the importance of detailed system-bath-memory structure in future quantum thermodynamic research.